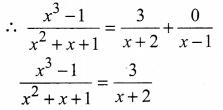You can Download Samacheer Kalvi 11th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 2 Basic Algebra Ex 2.9
Get the free “Partial Fraction Calculator” widget for your website, blog, WordPress, Blogger, or iGoogle.
Resolve the following rational expressions into partial fractions
Question 1.
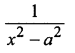
Solution:

Question 2.
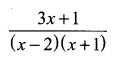
Solution:

![]()
Question 3.
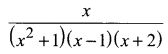
Solution:
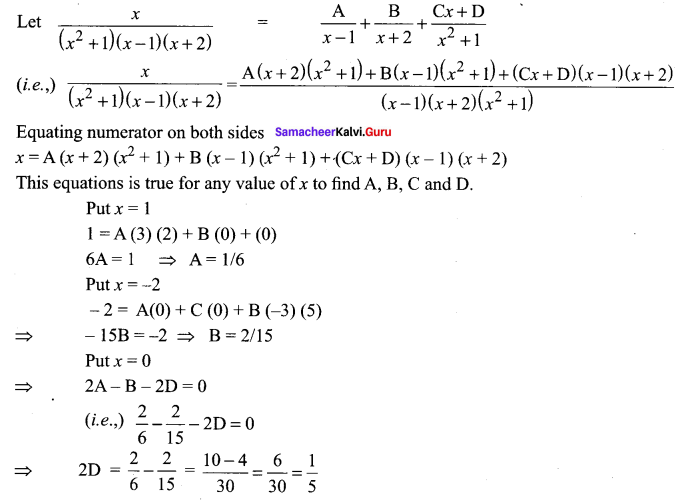
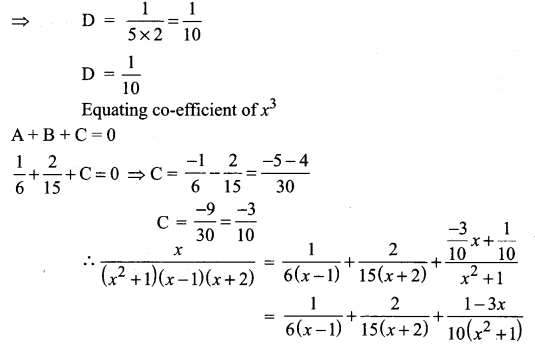
Question 4.
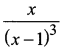
Solution:
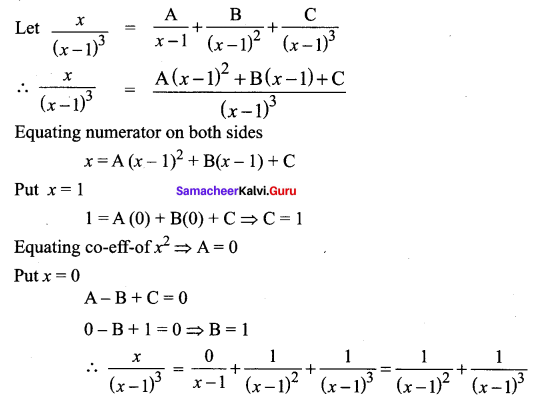
![]()
Question 5.
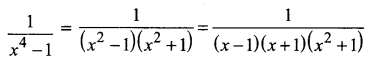
Solution:
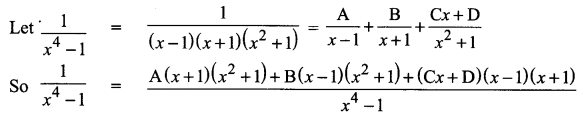
Equating nuemarator on bothsides we get

Question 6.
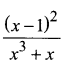
Solution:
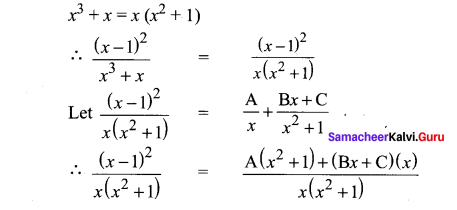
Equating numerator on both sides
(x – 2)2 = A(x2 + 1) + (Bx + c)(x)
Put x = 0
1 = A
Equating co-eff of x2
1 = A + B
(i.e.,) 1 + B = 1 ⇒ B = 0
put x = 1
A(2) + B + C = 0 (i.e.,) 2A + B + C = 0
2 + 0 + C = 0 ⇒ C = -2
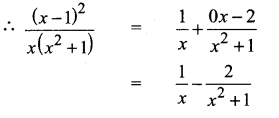
Question 7.
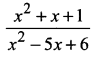
Solution:
Since numerator and denominator are of same degree
we have divide the numerator by the denominator
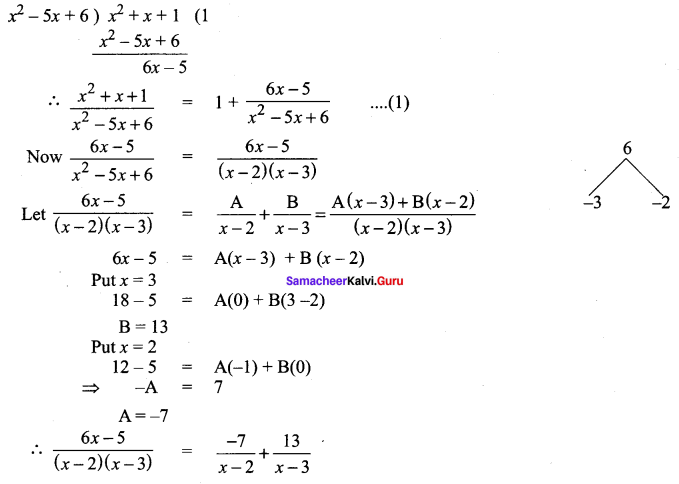
Substituting the value in ….(1)
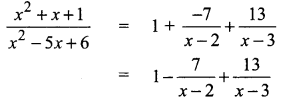
![]()
Question 8.
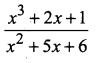
Solution:
Numerator is of greater degree than the denominator
So dividing Numerator by the denominator

⇒ 21x + 31 = A(x + 3) + B(x + 2)
Put x = -3
-63 + 31 = B(-1)
B = 32
Put x = -2
-42 + 31 = A(1) + B(0)
A = -11
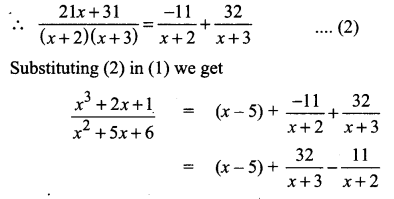
Question 9.
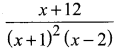
Solution:

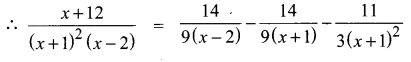
![]()
Question 10.
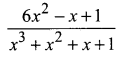
Solution:
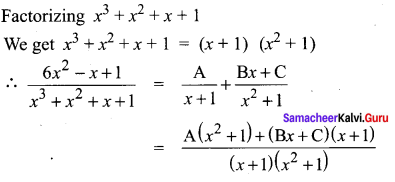
Equating Numerator on both sides we get
6x2 – x + 1 = A(x2 + 1) + (Bx + c)(x + 1)
6 + 1 + 1 = A(2) + 0 ⇒ 2A = 8 ⇒ A = 4
Equating co-eff of x2
6 = A + B
(i.e.,) 4 + B = 6 ⇒ B = 6 – 4 = 2
put x = 0
1 = A+ C
4 + C = 1 ⇒ C = 1 – 4 = -3
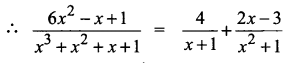
![]()
Question 11.
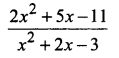
Solution:
Since Numerator and are of same degree divide Numerator by the denominator

equating Numerator on both sides we get
x – 5 = A(x + 3) + B(x – 1)
Put x = -3
-3 -5 = A(0) + B(-4)
-4B = -8 ⇒ B = 2
Put x = 1
1 – 5 = A(4) + B(0)
4A = -4 ⇒ A = -1
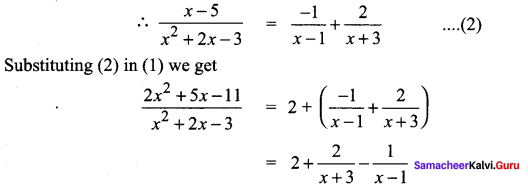
Question 12.
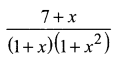
Solution:

Samacheer Kalvi 11th Maths Solutions Chapter 2 Basic Algebra Ex 2.9 Additional Questions
Question 1.
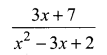
Solution:
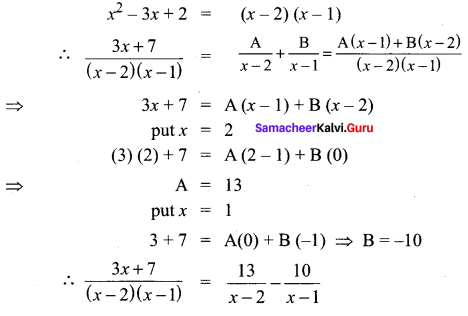
![]()
Question 2.
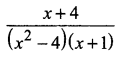
Solution:

Question 3.
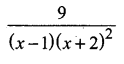
Solution:
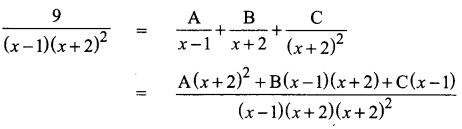
Equating nemerator on b/s
9 = A(x+2)2 + B(x – 1)(x + 2) + C(x – 1)
Put x = -2
9 = A(0) + B(0) + C(-3)
-3C = 9 ⇒ C = -3
Put x = 1
9 = A (1 + 2)2 + B (0) + C(0)
9A = 9
A = 1
Put x = 0
9 = 4A – 2B – C
9 = 4(1) – 2B + 3
9 – 7 = -2B
2 = -2B
B = -1
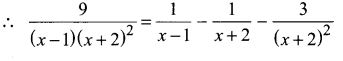
![]()
Question 4.
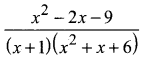
Solution:

Question 5.
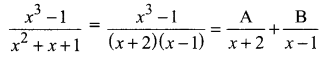
Solution:
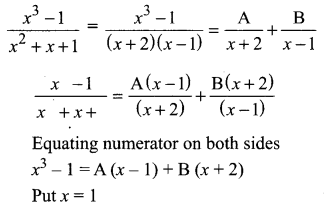
0 = 0 + B(1 + 2)
3B = 0 ⇒ B = 0
Put x = -2
(-2)3 – 1 = A(-2 – 1) + B(0)
-8 – 1 = -3A
-9 = -3A
A = 9/3 ⇒ A = 3