Students can Download Maths Chapter 1 Rational Numbers Additional Questions and Answers, Notes Pdf, Samacheer Kalvi 8th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.
![]()
Tamilnadu Samacheer Kalvi 8th Maths Solutions Term 1 Chapter 1 Rational Numbers Additional Questions
Additional Questions And Answers
Exercise 1.1
Very Short Answers [2 Marks]
Question 1.
Add \(\frac{3}{5}\) and \(\frac{13}{5}\)
Solution:
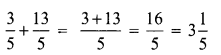
Question 2.
Add \(\frac{7}{9}\) and \(\frac{-12}{9}\)
Solution:
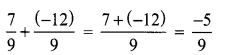
Question 3.
Add \(\frac{-3}{7}\) and \(\frac{-17}{7}\)
Solution:
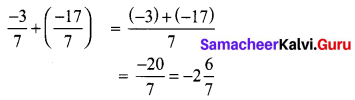
Question 4.
Add \(\frac{4}{-13}\) and \(\frac{7}{13}\)
Solution:
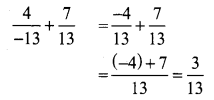
![]()
Question 5.
Subtract \(\frac{3}{4}\) and \(\frac{7}{4}\)
Solution:
\(\frac{7}{4}-\frac{3}{4}=\frac{7-3}{4}=\frac{4}{4}\) = 1
Short Answers [3 Marks]
Question 1.
Add \(\frac{4}{-3}\) and \(\frac{8}{15}\)
Solution:

Question 2.
Simplify \(\frac{9}{-27}+\frac{18}{39}\)
Solution:
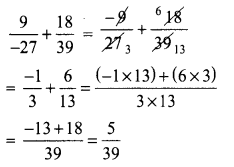
Long Answers [5 Marks]
Question 1.
By what number should we multiply \(\frac{3}{-14}\), so that the product may be \(\frac{5}{12}\)
Solution:
Let the number to be multiplied by x

∴ The number to be multiplied = \(\frac{-35}{18}\)
Question 2.
Simplify
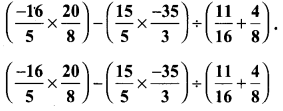
Solution:

Exercise 1.2
Very Short Answers [2 Marks]
Question 1.
Verify addition of rational number is closed using \(\frac{1}{4}\) and \(\frac{2}{3}\)
Solution:
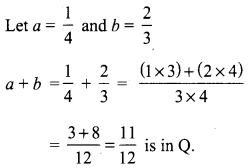
∴ Addition of rational numbers is closed
![]()
Question 2.
Is subtraction is commutative for rational numbers. Given an example.
Solution:
No, subtraction is not commutative for rational numbers.
Example: Let a = \(\frac{1}{2}\) and b = \(\frac{5}{6}\)

From (1) and (2)
a – b ≠ b – a for rational numbers
Very Short Answers [5 Marks]
Question 1.
Verify associative property for addition of rational numbers for a = \(\frac{5}{6}\), b = \(\frac{-3}{4}\), c = \(\frac{4}{7}\)
Solution:
Given a = \(\frac{5}{6}\), b = \(\frac{-3}{4}\), c = \(\frac{4}{7}\)

From (1) and (2) we have (a + b) + c = a + (b + c)
∴ Associative property is true for addition of rational numbers.
Question 2.
Verify distributive property of multiplication over addition for the rational numbers a = \(\frac{3}{4}\), b = \(\frac{-2}{3}\), c = \(\frac{3}{7}\)
Solution:
Given a = \(\frac{3}{4}\), b = \(\frac{-2}{3}\), c = \(\frac{3}{7}\)
To verify a × (b + c) = (a × b) + (a × c)
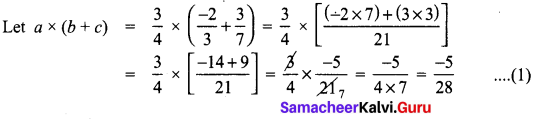
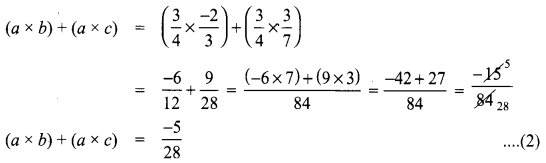
From (1) and (2)
a × (b + c) = (a × b) + (a × c)
∴ Distributive property of multiplication over addition is true for the given rational numbers.