You can Download Samacheer Kalvi 11th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 8 Vector Algebra – I Ex 8.1
Question 1.
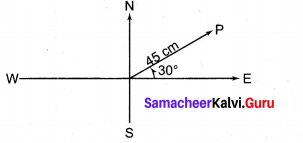
Represent graphically the displacement of
(i) 45 cm 30 ° north of east
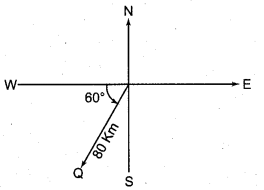
(ii) 80 km, 60° south of west
Solution:
(i) 45 cm 30 0 north of east
(ii) 80 km 60° south of west
Question 2.
Prove that the relation R defined on the set V of all vectors by \(\vec{a}\) R \(\vec{b}\) if \(\vec{a}=\vec{b}\) is an equivalence relation on V.
Solution:
\(\vec{a}\) R \(\vec{b}\) is given as \(\vec{a}=\vec{b}\).
(i) \(\vec{a}\) = \(\vec{a}\) ⇒ \(\vec{a}\) R \(\vec{a}\)
(i.e.,) the relation is reflexive.
(ii) \(\vec{a}=\vec{b}\) ⇒ \(\vec{b}\) = \(\vec{a}\)
(i.e.,) \(\vec{a}\) R \(\vec{b}\) – \(\vec{b}\) R \(\vec{a}\)
So, the relation is symmetric.
(iii) \(\vec{a}=\vec{b} ; \vec{b}=\vec{c} \Rightarrow \vec{a}=\vec{c}\)
(i.e) \(\vec{a}\) R \(\vec{b}\) ; \(\vec{b}\) R \(\vec{c}\) ⇒ \(\vec{a}\) R \(\vec{c}\)
So the given relation is transitive
So, it is an equivalence relation.
Question 3.
Let \(\vec{a}\) and \(\vec{a}\) be the position vectors of points A and B. Prove that the position vectors of the points which trisect the line segment AB are 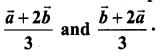
Solution:


![]()
Question 4.
If D and E are the midpoints of the sides AB and AC of a triangle ABC, prove that
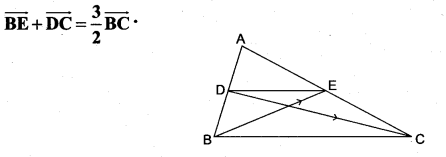
Solution:

Question 5.
Prove that the line segment joining the midpoints of two sides of a triangle is parallel to the third side whose length is half of the length of the third side.
Solution:


Question 6.
Prove that the line segments joining the midpoints of the adjacent sides of a quadrilateral form a parallelogram.
Solution:
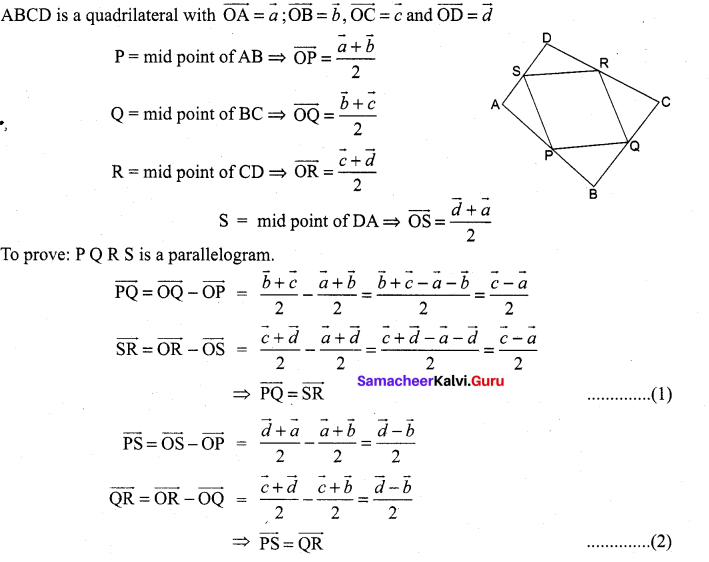
In a quadrilateral when opposite sides are equal and parallel it is a parallelogram So, PQRS is a parallelogram, from (1) and (2).
Question 7.
If \(\vec{a}\) and \(\vec{b}\) represent a side and a diagonal of a parallelogram, find the other sides and the other diagonal.
Solution:
OABC is a parallelogram where
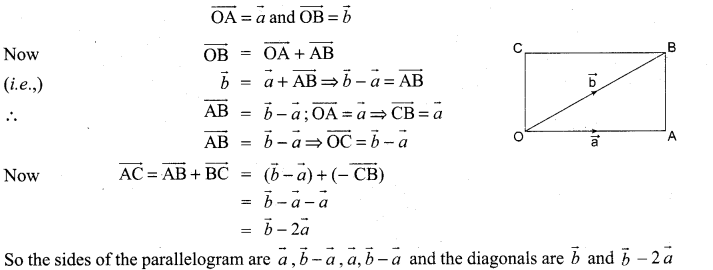
![]()
Question 8.
If \(\overrightarrow{\mathrm{PO}}+\overrightarrow{\mathrm{OQ}}=\overrightarrow{\mathrm{QO}}+\overrightarrow{\mathrm{OR}}\), prove that the points P, Q, R are collinear.
Solution:
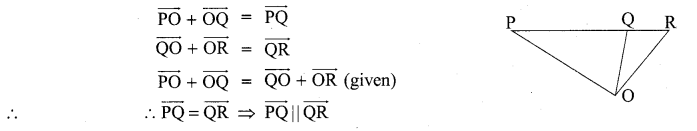
But Q is a common point.
⇒ P, Q, R are collinear.
Question 9.
If D is the midpoint of the side BC of a triangle ABC, prove that \(\overrightarrow{\mathbf{A B}}+\overrightarrow{\mathbf{A C}}=2 \overrightarrow{\mathbf{A D}}\)
Solution:
D is the midpoint of ∆ ABC.

Question 10.
If G is the centroid of a triangle ABC, prove that \(\overrightarrow{\mathrm{GA}}+\overrightarrow{\mathrm{GB}}+\overrightarrow{\mathrm{GC}}=0\)
Solution:
For any triangle ABC,
\(\overrightarrow{\mathrm{GA}}+\overrightarrow{\mathrm{GB}}+\overrightarrow{\mathrm{GC}}=0\)
Now G is the centroid of ∆ABC, which divides the medians (AD, BE and CF) in the ratio 2 : 1.

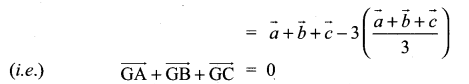
Question 11.
Let A, B, and C be the vertices of a triangle. Let D, E, and F be the midpoints of the sides BC, CA, and AB respectively. Show that \(\overrightarrow{\mathrm{AD}}+\overrightarrow{\mathrm{BE}}+\overrightarrow{\mathrm{CF}}=\overrightarrow{0}\)
Solution:
In ∆ABC, D, E, F are the midpoints of BC, CA, and AB respectively.

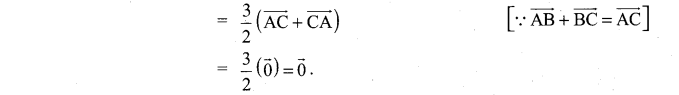
Question 12.
If ABCD is a quadrilateral and E and F are the midpoints of AC and BD respectively, then prove that \(\overrightarrow{\mathbf{A B}}+\overrightarrow{\mathbf{A D}}+\overrightarrow{\mathbf{C B}}+\overrightarrow{\mathbf{C D}}=4 \overrightarrow{\mathrm{EF}}\)
Solution:
ABCD is a quadrilateral in which E and F are the midpoints of AC and BD respectively.

Samacheer Kalvi 11th Maths Solutions Chapter 8 Vector Algebra – I Ex 8.1 Additional Problems
Question 1.
Shown that the points with position vectors ![]() are collinear.
are collinear.
Solution:
To prove the points P, Q, R are collinear we have to prove that \(\overrightarrow{\mathrm{PQ}}\) = t \(\overrightarrow{\mathrm{PR}}\) where t is a scalar.
Let the given points be P, Q, R.

So, the points P, Q, R are collinear (i.e,) the given points are collinear.
Question 2.
If ABC and A’B’C’ are two triangles and G, G’ be their corresponding centroids, prove that \(\overrightarrow{\mathrm{AA}^{\prime}}+\overrightarrow{\mathrm{BB}^{\prime}}+\overrightarrow{\mathrm{CC}^{\prime}}=3 \overrightarrow{\mathrm{GG}}\)
Solution:
Let O be the origin.
We know when G is the centroid of ∆ ABC,
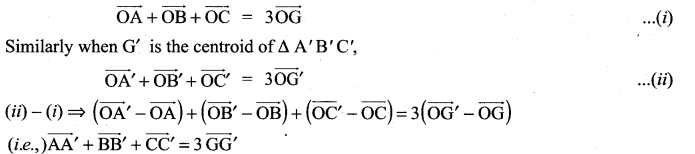
![]()
Question 3.
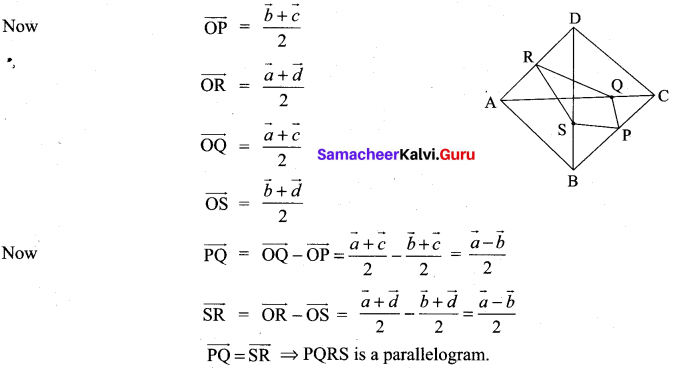
Prove using vectors the mid-points of two opposite sides of a quadrilateral and the mid-points of the diagonals are the vertices of a parallelogram.
Solution:
ABCD is a quadrilateral with position vectors
OA = \(\vec{a}\), OB = \(\vec{b}\), OC = \(\vec{c}\) and OD = \(\vec{d}\)
P is the midpoint of BC and R is the midpoint of AD.
Q is the midpoint of AC and S is the midpoint of BD.
To prove PQRS is a parallelogram. We have to prove that \(\overrightarrow{\mathrm{PQ}}=\overrightarrow{\mathrm{SR}}\)