You can Download Samacheer Kalvi 11th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 2 Basic Algebra Ex 2.10
Determine the region in the plane determined by the inequalities:
Question 1.
x ≤ 3y, x ≥ y
Solution:
Given in equation are x ≤ 3y,x ≥ y
Suppose x = 3y ⇒ \(\frac{x}{3}=\) = y
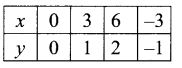
If x = y
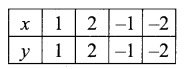
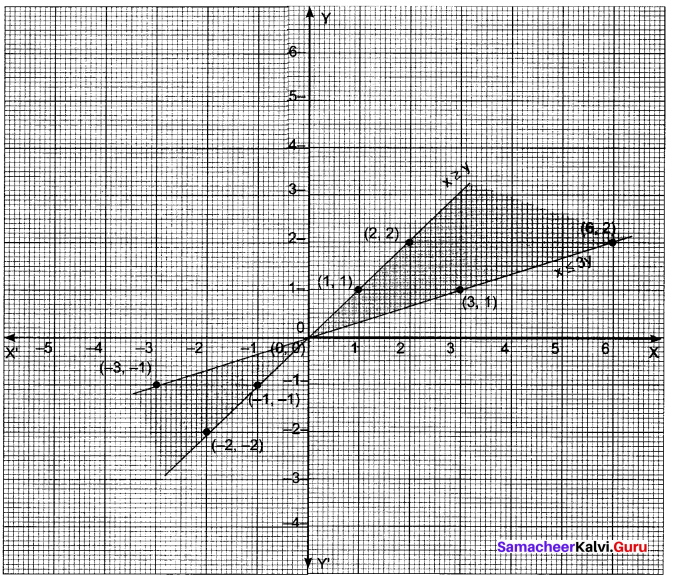
![]()
Question 2.
y ≥ 2x, -2x + 3y ≤ 6
Solution:
Suppose y = 2x
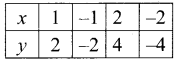
-2x + 3y = 6
-2x = 6 – 3y
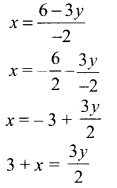
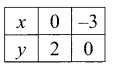
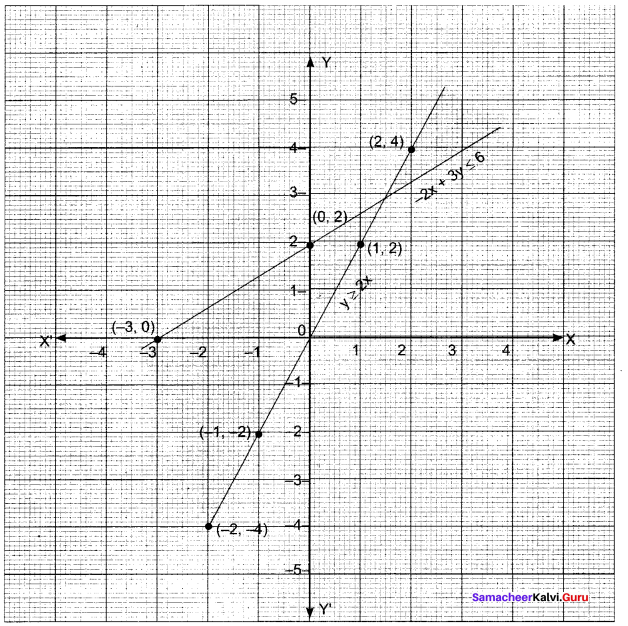
Question 3.
3x + 5y ≥ 45, x ≥ 0, y ≥ 0.
Solution:
If 3x + 5y = 45

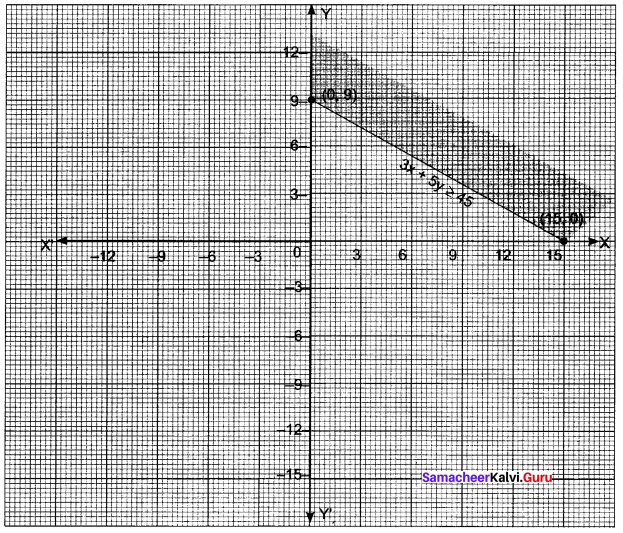
x ≥ 0 is nothing but the positive portion of Y-axis and y ≥ 0 is the positive portion of X-axis.
Shaded region is the required portions.
Question 4.
2x + 3y ≤ 35, y ≥ 2, x ≥ 5
Solution:
If 2x + 3y = 35 then
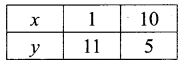
y = 2 is a line parallel to X-axis at a distance 2 units
x = 5 is a line parallel to Y-axis at a distance of 5 units
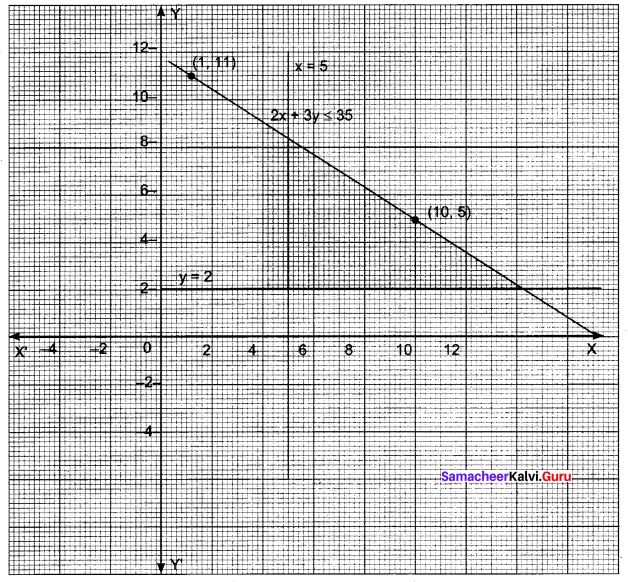
The required region is below 2x + 3y = 35, above y = 2 and to the right of x = 5
![]()
Question 5.
2x + 3y ≤ 6, x + 4y ≤ 4, x ≥ 0, y ≥ 0.
Solution:
If 2x + 3y = 6
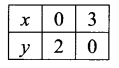
x + 4y = 4
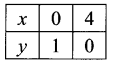
x ≥ 0, y ≥ 0 represents the area in the 1 quadrant.
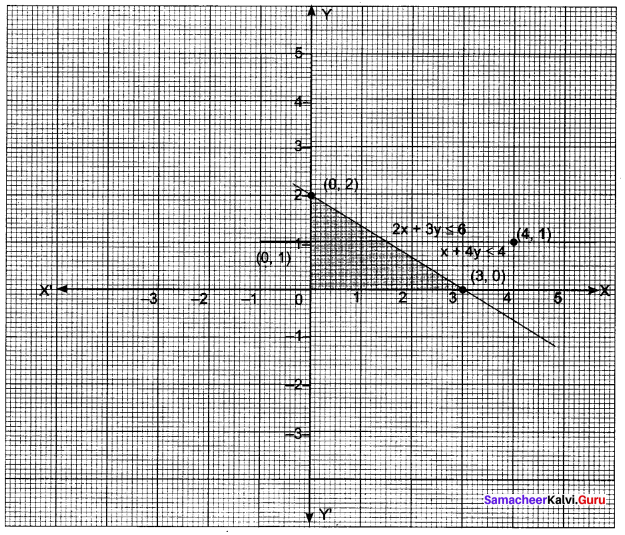
The required region is below 2x + 3y = 6 and below x + 4y = 4 bounded by x-axis and y-axis.
Question 6.
x – 2y ≥ 0, 2x – y ≤ -2, x ≥ 0, y ≥ 0
Solution:
If x – 2y = 0
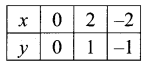
2x – y = -2
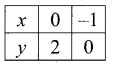
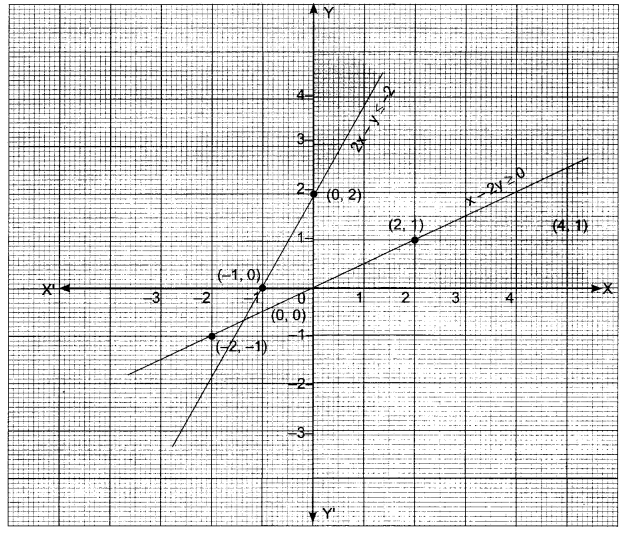
x ≥ 0, y ≥ 0 represents the portion in the 1 quadrant only.
Question 7.
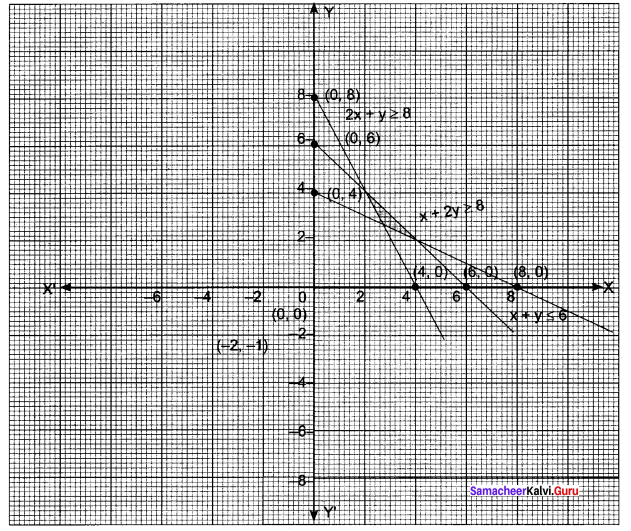
2x + y ≥ 8, x + 2y ≥ 8, x + y ≤ 6.
Solution:
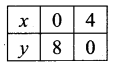
2x + y = 8
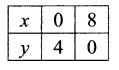
x + 2y = 8
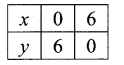
x + y = 6
Samacheer Kalvi 11th Maths Solutions Chapter 2 Basic Algebra Ex 2.10 Additional Questions
Question 1.
3x + 2y ≤ 12, x ≥ 1, y ≥ 2
Solution:
The given inequality is 3x + 2y ≤ 12.
Draw the graph of the line 3x + 2y ≤ 12
Table of values satisfying the equation
3x + 2y ≤ 12
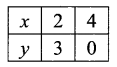
Putting (0, 0) in the given inequation, we have 3 × 0 + 2 × 0 ≤ 12
∴ Half plane of 3x + 2y ≤ 12 is towards origin
Also the given inequality is x ≥ 1.
Draw the graph of the line x = 1.
Putting (0, 0) in the given inequation, we have 0 ≥ 1 which is false.
∴ Half the plane of x ≥ 1 is away from the origin.
The given inequality is y ≥ 2.
Putting (0, 0) in the given inequation, we have 0 ≥ 2 which is false.
∴ Half plane of y ≥ 2 is away from the origin.
![]()
Question 2.
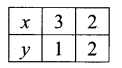
x + y ≥ 4, 2x – y > 0
Solution:
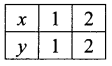
The given inequality is x + y ≥ 4.
Draw the graph of the line x + y = 4.
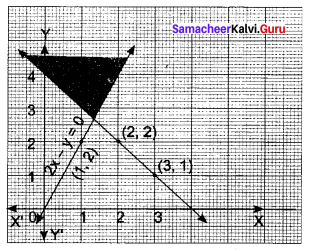
Table of values satisfying the equation
x + y = 4
Putting (0, 0) in the given inequation, we have 0 + 0 ≥ 4 ⇒ 0 ≥ 4, which is false.
∴ Half plane of x + y ≥ 4 is away from the origin.
Also the given inequality is 2x – y > 0.
Draw the graph of the line 2x – y = 0.
Table of values satisfying the equation
2x – y = 0
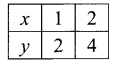
Putting (3, 0) in the given inequation, we have 2 × 3 – 0 > 0 ⇒ 6 > 0, which is true.
∴ Half plane of 2x – y > 0 containing (3, 0)
Question 3.
x + y ≤ 9, y > x, x ≥ 0
Solution:
The given inequality is x + y ≤ 9.
Draw the graph of the line x + y = 9.
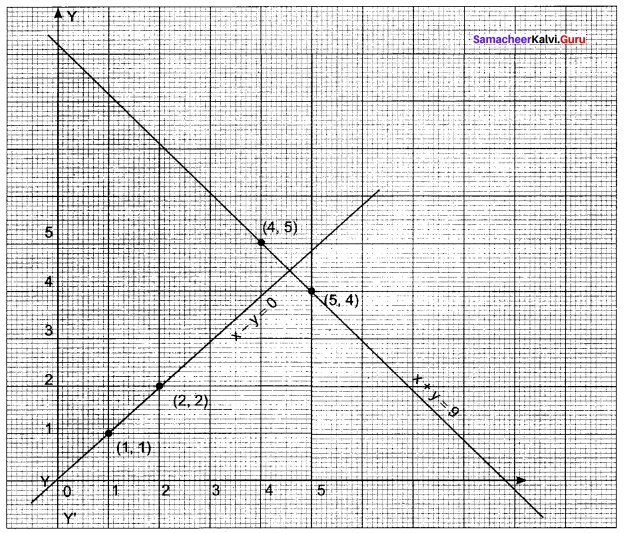
Table of values satisfying the equation
x + y = 9
Putting (0, 0) in the given inequation, we have 0 + 0 ≤ 9⇒ 0 ≤ 9, is towards is the origin.
∴ Half plane of x + y ≤ 9 is away from the origin.
Also, the given inequality is x – y < 0.
Draw the graph of line x -y = 0.
Table of values satisfying the equation
x – y = 0
Putting (0, 3) in the given inequation, we have 0 – 3 – 0 < 0 ⇒ -3 < 0, which is true.
∴ Half plane of x – y < 0 containing the points (0, 3).
![]()
Question 4.
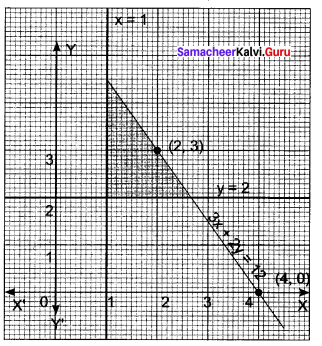
5x + 4y ≤ 20, x ≥ 1, y ≥ 2
Solution:
The given inequality is 5x + 4y ≤ 20.
Draw the graph of the line 5x + 4y = 20.
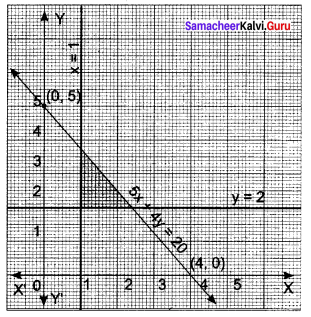
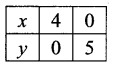
Table of values satisfying the equation
5x + 4y = 20
Putting (0, 0) in the given inequation, we have 5 × 0 + 4 × 0 ≤ 20 ⇒ 0 ≤ 20, which is true.
∴ Half plane of 5x + 4y ≤ 20 is away from the origin.
Also, the given inequality is x ≥ 1.
Draw the graph of the line x = 1.
Putting (0, 0) in the given inequation, we have 0 ≥ 1, which is false.
∴ Half plane of x ≥ 1 is y ≥ 2.
Draw the graph of the line y = 2.
Putting (0, 0) in the given inequation, we have 0 ≥ 2, which is false.
∴ Half plane of y ≥ 2 is away from the origin.
![]()
Question 5.
3x +4y ≤ 60, x + 3y ≤ 30, x ≥ 0, y ≥ 0
Solution:
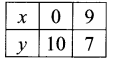
The given inequality is 3x + 4y ≤ 60.
Draw the graph of the line 3x + 4y = 60.
Table of values satisfying the equation
3x + 4y = 60
Putting (0, 0) in the given inequation, we have 3 × 0 + 4 × 0 ≤ 60 ⇒ 0 ≤ 60, which is true.
∴ Half the plane of 3x + 4y ≤ 60 is towards the origin.
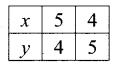
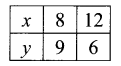
Also, the given inequality is x + 3y ≤ 30.
Draw the graph of the line x + 3y = 30.
Table of values satisfying the equation.
x + 3y = 30
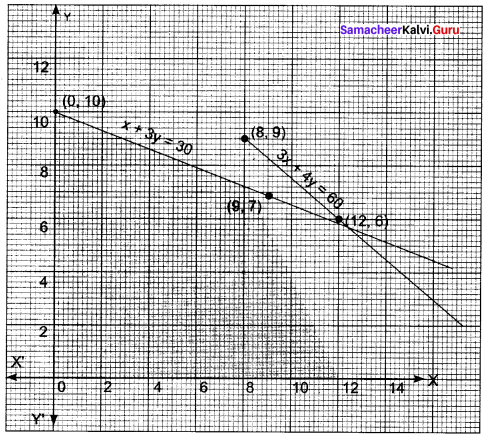
Putting (0, 0) in the given inequation, we have 0 + 3 × 0 ≤ 30 ⇒ 0 ≤ 30, which is true.
∴ Half plane of x + 3y ≤ 30 is towards the origin.