Students can Download Chemistry Chapter 7 Thermodynamics Questions and Answers, Notes Pdf, Samacheer Kalvi 11th Chemistry Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 11th Chemistry Solutions Chapter 7 Thermodynamics
Samacheer Kalvi 11th Chemistry Thermodynamics Textual Evaluation Solved
I. Choose the correct answer from the following:
Question 1.
The amount of heat exchanged with the surrounding at constant temperature and pressure is called ………
(a) ΔE
(b) ΔH
(c) ΔS
(d) ΔG
Answer:
(b) ΔH
Question 2.
All the naturally occurring processes proceed spontaneously in a direction which leads to
(a) decrease in entropy
(b) increase in enthalpy
(c) increase in free energy
(d) decrease in free energy
Answer:
(d) decrease in free energy
Question 3.
In an adiabatic process, which of the following is true?
(a) q = w
(b) q = 0
(c) ΔE = q
(d) PΔV = 0
Answer:
(a) q = 0
Question 4.
In a reversible process, the change in entropy of the universe is ‘
(a) >0
(b) > 0
(c) < 0
(d) = 0
Answer:
(d) = 0
Question 5.
In an adiabatic expansion of an ideal gas
(a) w = -∆u
(b) w = ∆u + ∆H
(c) ∆u = 0
(d) w = 0
Answer:
(a) w = -∆u
Question 6.
The intensive property among the quantities below is
(a) mass
(b) volume
(c) enthalpy
(d) mass/volume
Answer:
(d) mass/volume
![]()
Question 7.
An ideal gas expands from the volume of 1 x 10-3 m3 to 1 x 10-2 m3 at 300K against a constant pressure at 1 x 105 Nm-2. The work done is ………..
(a) – 900 J
(b) 900 kJ
(c) 270 kJ
(d) – 900 kJ
Answer:
(a) – 900 J
Hint:
w = – P∆V
w = – (1 x 105 Nm-2) (1 x 10-2 m3 – 1 x 10-3 m3)
w = – 105 (10-2– 10-3)Nm
w = – 105 (10 – 1) 103-) J
w = – 105(9x 10-3) J
w = – 9 x 102 J
w = – 900 J
Question 8.
Heat of combustion is always
(a) positive
(b) negative
(c) zero
(d) either positive or negative
Answer:
(b) negative
Question 9.
The heat of formation of CO and CO2 are -26.4 kcal and -94 kcal, respectively. Heat of combustion of carbon monoxide will be
(a) +26.4 kcal
(b) -67.6 kcal
(c) -120.6 kcal
(d) +52.8 kcal
Answer:
(b) -67.6 kcal
Hint:
CO(g) + O2(g) → CO2(g)
∆HC0 (CO) = [∆Hf(CO2) – ∆Hf(CO) + ∆Hf(O2)]
∆HC0 (CO) = -94 KCal – [- 26.4 KCal + 0]
∆HC0 (CO) = -94 KCal + 26.4 KCal
∆HC0 (CO) = -67.4 KCal
Question 10.
C(diamond) → C(graphite), ∆H = -ve, this indicates that ………..
(a) graphite is more stable than diamond
(b) graphite has more energy than diamond
(c) both are equally stable
(d) stability cannot be predicted
Answer:
(a) graphite is more stable than diamond
![]()
Question 11.
The enthalpies of formation of Al2O3 and Cr2O3 are -1596 kJ and -1134 kJ, respectively. ∆H for reaction 2Al + Cr2O3 → 2Cr + Al2O3 is ……….
(a) -1365 kJ
(b) 2730 kJ
(c) -2730 kJ
(d) -462 kJ
Answer:
(d) -462 kJ
Answer:
2A1 + Cr2O3 → 2Cr + Al2O3
∆Hr0 = [2 ∆Hf (Cr) + ∆Hf (Al2O3)] – [2 ∆Hf (Al) + ∆Hf (Cr2O2)]
∆Hr0 = [0 + (- 1596 kJ)] – [0 + (- 1134)]
∆Hr0 = – 1596 kJ + 1134 kJ
∆Hr0 = – 462 kJ
Question 12.
Which of the following is not a thermodynamic function?
(a) internal energy
(b) enthalpy
(c) entropy
(d) frictional energy
Answer:
(d) frictional energy
Question 13.
If one mole of ammonia and one mole of hydrogen chloride are mixed in a closed container to form ammonium chloride gas, then …………
(a) ∆H > ∆U
(b) ∆H – ∆U = 0
(c) ∆H + ∆U = 0
(d) ∆H < ∆U
Answer:
(d) ∆H < ∆U
Question 14.
Change in internal energy, when 4 kJ of work is done on the system and 1 kJ of heat is given out by the system is ………….
(a) +1 kJ
(b) -5 kJ
(c) +3 kJ
(d) -3 kJ
Answer:
(c) +3 kJ
Hint:
∆U = q + w
∆U = – 1 kJ + 4 kJ
∆U = + 3 kJ
![]() c
c
Question 15.
The work done by the liberated gas when 55.85 g of iron (molar mass 55.85 g mol-1) reacts with hydrochloric acid in an open beaker at 25°C …………
(a) -2.48 kJ
(b) -2.22 kJ
(c) +2.22 kJ
(d) + 2.48 kJ
Answer:
(a)-2.48 kJ
Hint:
Fe + 2HCl → FeCl2 + H2
1 mole of Iron liberates 1 mole of hydrogen gas
55.85 g Iron = 1 mole Iron
∴ n = 1
T = 25°C = 298 K
w = -P\(\left(\frac{\mathrm{nRT}}{\mathrm{P}}\right)\)
w = -nRT
w = -1 x 8314 x 298 J
w = 2477.57 J
w = -2.48 k J
Question 16.
The value of AH for cooling 2 moles of an ideal monoatomic gas from 125°C to 25°C at constant pressure will be [given CP = \(\frac {5}{2}\) R] …………..
(a) -250 R
(b) -500 R
(c) 500 R
(d) +250 R
Answer:
(b) -500 R
Hint:
Ti = 125°C = 398K
Tf = 25°C = 298 K
∆H = nCp (Tf – Ti)
∆H = 2 x \(\frac {5}{2}\)R (298 – 398)
∆H = -500 R
Question 17.
Given that C(g) + O2(g) → CO2(g) ∆H°= a kJ; 2 CO(g) + O2(g) → 2CO2(g) ∆H° = -b kJ; Calculate the ∆H° for the reaction C(g) + H2O2(g) → CO(g)
(a) \(\frac {b + 2a}{2}\)
(b) 2a – b
(c) \(\frac {2a – b}{2}\)
(d) \(\frac {b – 2a}{2}\)
Answer:
(d) \(\frac {b – 2a}{2}\)
Hint:
C + O2 → CO2 ∆H° = -a kJ ……..(1)
2CO + O2 → 2CO2 ∆H° = -b kJ …….(2)
C + ½O2 → CO ∆H° = ?
(1) x (2)
2C + 2O2 → 2CO2 ∆H° = -2a KJ …….(3)
Reverse of equestion (2) will be
2CO2 → 2CO + O2 ∆H° = +b KJ …….(4)
(3) + (4)
2C + O2 → 2CO ∆H° = b – 2a KJ …….(5)
(5) ÷ 2
C + O2 → CO ∆H° = \(\frac {b – 2a}{2}\) KJ
![]()
Question 18.
When 15.68 litres of a gas mixture of methane and propane are fully combusted at 0°C and 1 atmosphere, 32 litres of oxygen at the same temperature and pressure are consumed. The amount of heat released from this combustion in kJ is (∆HC (CH4) = – 890 kJ mol-1 and ∆HC (C3H8) = -2220 kJ mol-1)
(a) -889 kJ
(b) -1390 kJ
(c) -3180 kJ
(d) -653.66 kJ
Answer:
(d) -653.66 kJ
Hint:
Given,
∆HC (CH4) = -890 kJ mol-1
∆HC (C3H8) = -2220 kJ mol-1
Let the mixture contain x lit of and lit of propane.
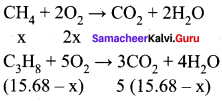
Volume of oxygen consumed = 2 x + 5 (15.68 – x) = 32 lit
2x + 78.4 – 5 x = 321
78.4 – 3x = 32
3x = 46.41
x = 15.471
Given mixture contains 15.47 liters of methane and 0.2 13 liters of propane. Hence,
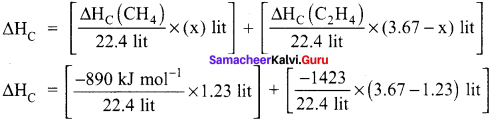
∆HC = [- 614.66 kJ mol-1] + [- 20.81 kJ mol-1]
∆HC = 635.47 kJ mol-1.
Question 19.
The bond dissociation energy of methane and ethane are 360 kJ mol-1 and 620 Id mol-1 respectively. Then, the bond dissociation energy of C-C bond is …………
(a) 170 kJ mol-1
(b) 50 kJ mol-1
(c) 80 kJ mol-1
(d) 220 kJ mol-1
Answer:
(c) 80 kJ mol-1
Hint:
4EC-H = 360 kJ mol-1
EC-H = 90 kJ mol-1
EC-C + 6EC-H = 620 KJ mol-1
EC-C + 6 x 9O = 62O kJ mol-1
EC-C + 540 = 620 kJ mol-1
EC-C = 80 kJ mol-1
Question 20.
The correct thermodynamic conditions for the spontaneous reaction at all temperature is (NEET phase – I)
(a) ∆H<0 and ∆S>0
(b) ∆H<0 and ∆S<0
(c) ∆S>0 and ∆S = 0
(d) ∆H<0 and ∆S>0
Answer:
(a) ∆H<0 and ∆S>0
![]()
Question 21.
The temperature of the system decreases in an …………
(a) isothermal expansion
(b) isothermal compression
(c) adiabatic expansion
(d) adiabatic compression
Answer:
(c) adiabatic expansion
Question 22.
In an isothermal reversible compression of an ideal gas the sign of q, AS and w are respectively
(a) +, -, –
(b) -, +, –
(c) +, -, +
(d) -, -, +
Answer:
(d) -, -, +
Hint:
During compression, the energy of the system increases, in isothermal condition, to maintain the temperature constant, heat is liberated from the system. Hence q is negative. During compression, entropy decreases. During compression work is done on the system, hence w is positive.
Question 23.
The molar heat of vaporization of a liquid is 4.8 kJ mol-1. If the entropy change is 16 J mol-1 K-1. the boiling point of the liquid is ………..
(a) 323 K
(b) 27°C
(c) 164 K
(d) 0.3 K
Answer:
(b) 27°C
Hint:

Question 24.
∆S is expected to be maximum for the reaction
(a) Ca(S) + O2(g) → CaO(S)
(b) C(S) + O2(g) → CO2(g)
(c) N2(g) + O2(g) → 2NO(g)
(d) CaCO3(S) → CaO(S) + CO2(g)
Answer:
(d) CaCO3(S) → CaO(S) + CO2(g)
Hint:
In CaCO3(S) → CaO(S) + CO2(g) entropy change is positive in (a) and (b) entropy change is negative; in (c) entropy change is zero.
Question 25.
The values of H and S for a reaction are respectively 30 kJ mol-1 and loo kJ mol-1. Then the temperature above which the reaction will become spontaneous is ………….
(a) 300 K
(b) 30 K
(c) 100 K
(d) 20°C
Answer:
(a) 300 K
Hint:
∆G = ∆H – T∆S
At 300 K.
∆G = 30000 J mol-1 – 300 K x 100 JK mol-1
∆G = 0
above 300 K;
∆G will be negative and reaction becomes spontaneous.
![]()
II . Answer these questions briefly.
Question 26.
State the first law of thermodynamics.
Answer:
The first law of thermodynamics, known as the law of conservation of energy, states that the total energy of an isolated system remains constant though it may change from one form to another.
The mathematical statement of the First Law as:
∆U = q + w
where q – the amount of heat supplied to the system; w – work done on the system.
Question 27.
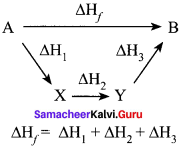
Define Hess’s law of constant heat summation.
Answer:
Hess’s law:
The enthalpy change of a reaction either at constant volume or constant pressure is the same whether it takes place in a single or multiple steps.
Question 28.
Explain intensive properties with two examples.
Answer:
The property that is independent of the mass or the size of the system is called an intensive property. Refractive index, Surface tension, density, temperature, Boiling point, Freezing point, molar volume.
Question 29.
Define the following terms:
(a) isothermal process
(b) adiabatic process
(c) isobaric process
(d) isochoric process
Answer:
a. An isothermal process is defined as one in which the temperature of the system remains constant, during the change from its initial to final state. The system exchanges heat with its surroundings and the temperature of the system remains constant. For an isothermal process dT = 0.
b. An adiabatic process is defined as one in which there is no exchange of heat (q) between the system and surrounding during the process. Those processes in which no heat can flow into or out of the system are called adiabatic processes.
c. An isobaric process is defined as one in which the pressure of the system remains constant
during its change from the initial to final state.
For an isobaric process dP = 0.
d. An isochoric process is defined as the one in which the volume of system remains constant during its change from initial to final state. Combustion of fuel in a bomb calorimeter is an example of an isochoric process.
For an isochoric process, dV= 0.
![]()
Question 30.
What is the usual definition of entropy? What ¡s the unit of entropy?
Answer:
- Entropy is a thermodynamic state function that is a measure of the randomness or disorderliness of the system.
- For a reversible change taking place at a constant temperature (T). the change in entropy
- of the system is equal to heat energy absorbed or evolved (q) by the system divided by the constant temperature (T).
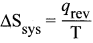
- SI unit of entropy is J K-1
Question 31.
Predict the feasibility of a reaction when
- both ∆H and ∆S positive
- both ∆H and ∆S negative
- AH decreases but ∆S increases
Answer:
- ∆Hr = + ve, ∆S = + ve; non-spontaneous at low temperature spontaneous at high temperature
- ∆Hr = – ve, ∆S = – ve; spontaneous at low temperature non-spontaneous at high temperature
- ∆H decreases but ∆S increases = Spontaneous at all temperatures.
Question 32.
Define Gibb’s free energy.
Answer:
G is expressed as G = H – TS, free energy change of a process is given by the relation ∆G = ∆H – T∆S.
Question 33.
Define enthalpy of combustion.
Answer:
Enthalpy of combustion of a substance is defined as “the change in enthalpy of a system when one mole of the substance is completely burnt in excess of air or oxygen”. it is denoted as AH.
Question 34.
Define molar heat capacity. Give its unit.
Answer:
Molar heat capacity is defined as “the amount of heat absorbed by one mole of a substance in raising the temperature by I Kelvin”. It is denoted as Cm
Unit of Molar heat capacity: SI unit of Cm is JK-1 mol-1.
![]()
Question 35.
Define the calorific value of food. What is the unit of calorific value?
Answer:
- The calorific value of food is defined as the amount of heat produced in calories (or Joules) when one gram of food is completely burnt.
- Unit of calorific value (a) Cal g-1 (b) J Kg-1
Question 36.
Define enthalpy of neutralization.
Answer:
The heat of neutralization is defined as “The change in enthalpy when one gram equivalent of an acid is completely neutralized by one gram equivalent of a base or vice versa in dilute solution”.
HCl(aq) + NaOH(aq) → NaCl(aq) + H2O
∆H = – 57.32 kJ
Question 37.
What is lattice energy?
Answer:
Lattice energy is defined as the amount of energy required to completely separate one mole of a solid ionic compound into a gaseous constituent.
Question 38.
What are state and path functions? Give two examples.
Answer:
State function:
A state function is a thermodynamic property of a system, which has a specific value for a given state and does not depend on the path (or manner) by which the particular state is reached.
Example:
Pressure (P), Volume (V), Temperature(T), Internal energy (U), Enthalpy (H), free energy (G) etc.
Path functions:
A path function is a thermodynamic property of the system whose value depends on the path by which the system changes from its initial to final states.
Examples: Work (w), Heat (q).
Question 39.
Give Kelvin a statement of the second law of thermodynamics.
Answer:
It is impossible to construct a machine that absorbs heat from a hot source and converts it completely into work by a cyclic process without transferring a part of heat to a cold sink.
Question 40.
The equilibrium constant of a reaction is 10, what will be the sign of ∆G? Will this reaction be spontaneous?
Answer:
∆G° = -2.303 RT log Keq
Keq = 10
∴ ∆G° = -ve value.
So the reaction will be spontaneous.
Question 41.
Enthalpy of neutralization is always a constant when a strong acid is neutralized by a strong base: account for the statement.
Answer:
It is because in dilution solution all strong acids and strong bases are completely ionized. The neutralization of strong acid and strong bases are completely ionized. The neutralization of a strong acid and strong base simply involves the combination of H+ ions (from acid) and OH– ions (from base) to form unionized water molecules with the evolution of 57.1 kJ heat.
H+(aq) + OH–(aq) → H2O(l),
∆2H° = -57.1 kJ
Since the same reaction takes place during neutralization of all strong acids and strong bases, the value of enthalpy of neutralization is constant.
![]()
Question 42.
State the third law of thermodynamics.
Answer:
It states that the entropy of pure crystalline substance at absolute zero is zero.
(or)
It can be stated as “it is impossible to lower the temperature of an object to absolute zero in a
finite number of steps”. Mathematically ![]()
Question 43.
Write down the Born-Haber cycle for the formation of CaCl2
Answer:
Born – Haber cycle for the formation of CaCl2
Ca(S) + Cl2(l) → CaC2(S) ∆Hf°
Sublimation : Ca(S) → Ca(S) ∆H1°
Ionization : Ca(g) → Ca2+(g) + 2e– = ∆H2°
Vapourisation : Cl2(l) → Cl2(g) = ∆H3°
Dissociation : Cl2(g) → 2Cl(g) = ∆H4°
Electron affinity : 2Cl2(g) + 2e– → 2Cl–2(g)(g) = ∆H5°
Lattice enthalpy : Ca2+(g) + 2Cl–(g) → CaCl2(S) = ∆H6°
∆Hf° = ∆H1° + ∆H2° + ∆H3° + ∆H4° + ∆H5° + ∆H6°
Question 44.
Identify the state and path functions out of the following
(a) Enthalpy
(b) Entropy
(c) Heat
(d) Temperature
(e) Work
(f) Free energy.
Answer:
State function: Enthalpy, entropy, temperature, and free energy.
Path function: Heat and work.
![]()
Question 45.
State the various statements of the second law of thermodynamics.
Answer:
Entropy statement:
The second law of thermodynamics can be expressed in terms of entropy, i.e “the entropy of an isolated system increases during a spontaneous process”.
Kelvin-Planck statement:
It is impossible to construct a machine that absorbs heat from a hot source and converts it completely into work by a cyclic process without transferring a part of heat to a cold sink.
Clausius statement:
It is impossible to transfer heat from a cold reservoir to a hot reservoir without doing some work.
Question 46.
What are spontaneous reactions? What are the conditions for the spontaneity of a process?
Answer:
- A reaction that does occur under the given set of conditions is called a spontaneous reaction.
- The expansion of a gas into an evacuated bulb is a spontaneous process, the reverse process that is gathering of all molecules into one bulb is not spontaneous. This example shows that processes that occur spontaneously in one direction cannot take place in opposite
direction spontaneously. - Increase in randomness favours a spontaneous change.
- If enthalpy change of a process is negative, then the process is exothermic and occurs spontaneously. Therefore ∆H should be negative.
- if entropy change of a process is positive, then the process occurs spontaneously, therefore ∆S should be positive.
- If free energy of a process is negative, then the process occurs spontaneously, therefore ∆G should be negative.
- For a spontaneous. irreversible process. ∆H <0, ∆S > 0, ∆G < 0. i.e., ∆H = -ve, ∆S = +ve and ∆G = -ve.
Question 47.
List the characteristics of internal energy.
Answer:
The internal energy of a system is an extensive property. It depends on the amount of the substances present in the system. If the amount is doubled, the internal energy is also doubled.
The internal energy of a system is a state function. It depends only upon the state variables (T, P, V, n) of the system. The change in internal energy does not depend on the path by which the final state is reached.
The change in internal energy of a system is expressed as ∆U = Uf – Ui.
In a cyclic process, there is no internal energy change. ∆U(cyclic) = 0
If the internal energy of the system in the final state (Uf) is less than the internal energy of the system in its initial state (Ui), then ∆U would be negative.
∆U = Uf – Ui = -ve(Uf < Ui)
If the internal energy of the system in the final state (Uf) is greater than the internal energy of the system in its initial state (Ui), then ∆U would be positive.
∆U = Uf – Ui = + ve(Uf > Ui).
Question 48.
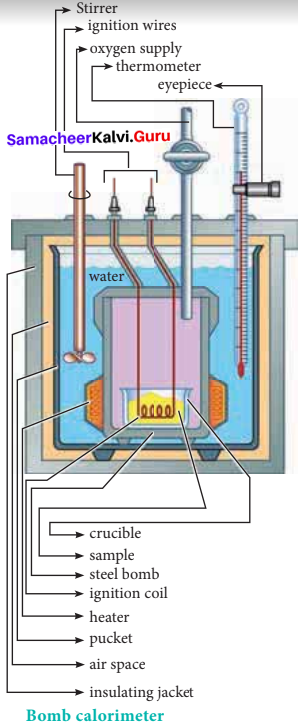
Explain how heat absorbed at constant volume is measured using a bomb calorimeter with a neat diagram.
Answer:
1. For chemical reactions, heal absorbed at constant volume, is measured in a bomb calorimeter.
2. Description of the apparatus and procedure:
The inner vessel and its cover are made of strong steel. The cover is fitted tightly to the vessel by means of metal lid and screws. A weighed amount of the substance is taken in a platinum cup connected with electrical wires for striking an arc instantly to kindle combustion. The bomb is then tightly closed and pressurizcd with excess
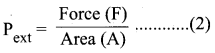
oxygen. The bomb is lowered in water, which is placed inside the calorimeter. A stirreris placed in the bomb to stir the water uniformly. The reaction is started by striking the substance through electrical heating.
3. During burning, the exothermic heat generated inside the bomb raises the temperature of the surrounding water bath. Temperature change can be measured accurately using Beckmann thermometer. Since the bomb calorimeter is sealed, its volume does not change, so the heat measurements, in this case, corresponds to the heat of reaction at constant volume.
4. In a bomb calorimeter experiment, a weighed sample of benzoic acid (w) is placed in the bomb which is then filled with excess oxygen and sealed. Ignition is brought about electrically. The rise in temperature (AT) is noted. Water equivalent or calorimetry equivalent of the calorimeter is known from the standard value of enthalpy of combustion of benzoic acid.
5. ∆HC(C6H5COOH) = -3227 kJ mol-1
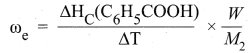
6. By knowing o value, the enthalpy of combustion of any other substance is determined adopting the similar procedure and using the substance in place of’ benzoic acid. By this experiment, the enthalpy of combustion at constant volume (AUC°) is known,
∆UC° = ωe. ∆T
7. Enthalpy of combustion at constant pressure of the substance is calculated from the equation
∆U°C(pressure) = ∆U°C(volume) + ∆ng RT
![]()
Question 49.
Calculate the work involved in the expansion and compression process.
Answer:
1. The essential condition of expansion or compression of a system is, there should be a difference between external pressure Pext and internal pressure (Pint).
2. If the volume of the system is increased against the external pressure. the work is done by the system. By convention work done by the system is given a negative sign (-w).
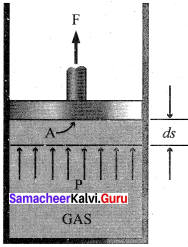
3. If the volume of the system decreased, the work is done on the system. By convention work done on the system is given a positive sign (+w).
4. For understanding pressure-volume work, let us consider a cylinder which contains one mole of an ideal gas fitted with a frictionless piston. Total volume of the gas is Vi and pressure of the gas inside is Pint.
5. If external pressure is Pext which is greater than Pint piston is moved inward till the pressure inside becomes equal to Pint It is achieved in a single step and the final volume be Vf.
6. During this compression, piston moves a distance x) and is the cross-sectional area of the piston is A, then, Change in volume = x A = ∆V = Vf – Vi ………..(1)
Pext = \(\frac {Force (F)}{Area(A)}\) ………(2)
F = Pext.A
7. if work is done by the system by pushing out the piston against external pressure (Pext) then according to the equation,
-w = F.x ………(3)
-w = Pext . A . x …….(4)
-w = Pext.∆V ……….(5)
-w = Pext . (Vf– Vi.) …..(6)
Simply w = – P∆V ………..(7)
8. From the above equation, we can predict the sign of work (w).
9. During expansion, work is done by the system, since Vf>Vi the sign obtained for work will be negative.
10. During compression, work is done on the system, since Vf<Vi the sign obtained for work will be positive.
Question 50.
Derive the relation between ∆H and ∆U for an ideal gas. Explain each term involved in the equation.
Answer:
When the system at constant pressure undergoes changes from an initial state with H1, U1 and V1 to a final state with H2, U2 and V2 the change in enthalpy
∆H can be calculated as follows:
H =U + PV
In the initial state
H1 = U1 + PV1 ………………(1)
In the final state
H2 = U2 + PV2 ……………..(2)
change in enthalpy is (2) – (1)
(H2 – H1) = (U2 – U1) + P(V2 – V1)
∆H = ∆U + P∆V ………………..(3)
As per first law of thermodynamics,
∆U = q + w
Equation (3) becomes
∆H = q + w+P∆V
w = -P∆V
∆H = qp – P∆V + P∆V
∆H = qp ………….(4)
qp – is the heat absorbed at constant pressure and is considered as heat content.
Consider a closed system of gases which are chemically reacting to form gaseous products at constant temperature and pressure with Vi and Vf, as the total volumes of the reactant and product gases respectively, and niand nfas the number of moles of gaseous reactants and products, then,
For reactants (initial state):
PVi = niRT ………..(5)
For products (final state):
PVf = nfRT ……………..(6)
(6) – (5)
P{Vf – Vi) = (nf – ni)RT
P∆V = ∆n(g) RT ………..(7)
Substituting in (7) in (3)
∆H = ∆U+ ∆n(g)RT …………….(8)
![]()
Question 51.
Suggest and explain an indirect method to calculate lattice enthalpy of sodium chloride crystal.
Answer:
The Born – Haber cycle is used to determine the lattice enthalpy of NaCl as follows:
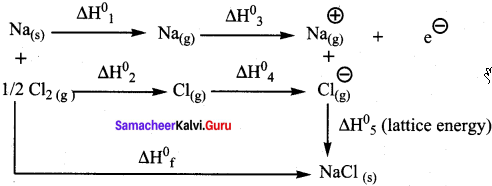
Formation of NaCl can be considered in 5 steps. The sum of the enthalpy changes of these steps is equal to the enthalpy change for the overall reaction from which the lattice enthalpy of NaCl is calculated.
Na(s) + Vi Cl2(g) → NaCl(s) ∆Hf = -411.3 kJ mol-1
Sublimation : Na(s) → Na(g) ∆H1°
Dissociation : ½ Cl2(g) → Cl(g) ∆H2°
Ionisation : Na(s) → Na+(g) + e– ∆H3°
E1etron affinity : Cl(g) + e– → Cl–(g) ∆H4°
Lattice enthalpy : Na+(g) + Cl–(g) → NaCl(s) ∆H5° =?
∆H = ∆H1° + ∆H4° + ∆H4° + ∆H4° + ∆H4°
∆H = ∆Hf° – (∆H1° + ∆H2°+ ∆H3°+∆H4°)
∆H5°= Lattice enthalpy of NaCl.
By the above method, indirectly lattice enthalpy of NaCl is calculated if the values of ∆Hf°, ∆H1°, ∆H2°- ∆H3° and ∆H4° are given.
Question 52.
List the characteristics of Gibbs free energy.
Answer:
(i) G is defined as (H-TS) where H and S are the enthalpy and entropy of the system respectively. T = temperature. Since H and S are state functions, G is a state function.
(ii) G is an extensive property while ∆G = (G2 – G1) which is the free energy change between the initial (1) and final (2) states of the system becomes the intensive property when mass remains constant between initial and final states (or) when the system is a closed system.
(iii) G has a single value for the thermodynamic state of the system.
(iv) G and ∆G values correspond to the system only. There are three cases of ∆G in predicting the nature of the process. When, ∆G < 0 (negative), the process is spontaneous and feasible; ∆G = 0. The process is in equilibrium and ∆G > 0 (positive), the process is nonspontaneous and not feasible.
(v) ∆G = ∆H – T∆S. But according to I law of thermodynamics,
∆H = ∆G + P∆V and ∆U = q + w
∴ ∆G = q + w + P∆V – T∆S
But ∆S = \(\frac{T}{q}\) and T∆S = q = heat involved in the process.
∴ ∆G = q + w + P∆V – q = w + P∆V
(or) – ∆G = – w – P∆V = network.
The decrease in free energy – ∆G, accompanying a process taking place at constant temperature and pressure is equal to the maximum obtainable work from the system other than work of expansion.
This quantity is called the “network” of the system and it is equal to (- w – P∆V).
∴ Network = – w – P∆V
-∆G represents all others forms of work obtainable from the system such as electrical, chemical or surface work etc other than P-V work.
Question 53.
Calculate the work done when 2 moles of an ideal gas expands reversibly and isothermally from a volume of 500 ml to a volume of 2 L at 25°C and normal pressure.
Answer:
Given
n = 2 moles
Vi = 500 ml = 0.5 lit
Vf = 2 lit
T = 25°C = 298 K
w = -2.303 nRT log \(\left(\frac{V}{V_{i}}\right)\)
w = -2.303 x 2 x 8.314 x 298 x log \(\frac {2}{0.5}\)
w = -2.303 x 2 x 8.314 x 298 x log(4)
w = -2.303 x 2 x 8.314 x 298 x 0.6021
w = -6871 J
w =-6.871 kJ.
![]()
Question 54.
In a constant-volume calorimeter, 3.5 g of gas with molecular weight 28 was burnt ¡n excess oxygen at 298 K. The temperature of the calorimeter was found to increase from 298 K to 298.45 K due to the combustion process. Given that the calorimeter constant is 2.5 kJ K-1. Calculate the enthalpy of combustion of the gas in kJ mol-1.
Answer:
Given
Ti = 298 K
Tf = 298.45 K
k = 2.5 kJ K-1
m = 3.5g
Mm = 28
heat evolved = k∆T
= k(Tf – Ti)
= 2.5KJ K-1 (298.45 – 298)K = 1.125 kJ
∆Hc = \(\frac{1.125}{3.5}\) × 28 kJ mol-1
∆Hc = 9 kJmol-1
Question 55.
Calculate the entropy change in the system and surroundings and the total entropy change in the universe during a process in which 245 J of heat flow out of the system at 77°C to the surrounding at 33°C.
Answer:
Given:
Tsys = 77°C = (77 + 273) = 350K
Tsys = 33°C = (33 + 273) = 306K
q = 245 J
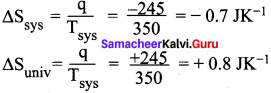
∆Suniv = ∆Ssys + ∆Ssurr-245 = —07 3K’
∆Suniv = -0.7 JK-1 + 0.8 JK-1
∆Suniv = 0.1 JK-1
Question 56.
1 mole of an ideal gas, maintained at 4.1 atm and at a certain temperature, absorbs heat 3710 J and expands to 2 litres. Calculate the entropy change in expansion process.
Answer:
Given,
n = 1 mole
P = 4.1 atm
V = 2Lit
T = ?
q = 3710 J
∆S = \(\frac {q}{T}\)
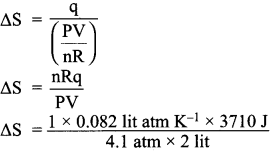
∆S = 37.10 JK-1
Question 57.
30.4 kJ is required to melt one mole of sodium chloride. The entropy change during melting is 28.4 JK-1 mol-1. Calculate the melting point of sodium chloride.
Answer:
Given,
∆Hf(NaCl) = 30.4 kJ = 30400 J mol-1
∆Sf (NaCl) = 28.4 JK-1 mol-1
Tf = ?

Tf = 1070.4 K.
![]()
Question 58.
Calculate the standard heat of formation of propane, if its heat of combustion is -2220.2 KJ mol-1, the heats of formation of CO2(g) and H2O(l) are – 393.5 and -285.8 kJ mol-1 respectively.
Answer:
Given,
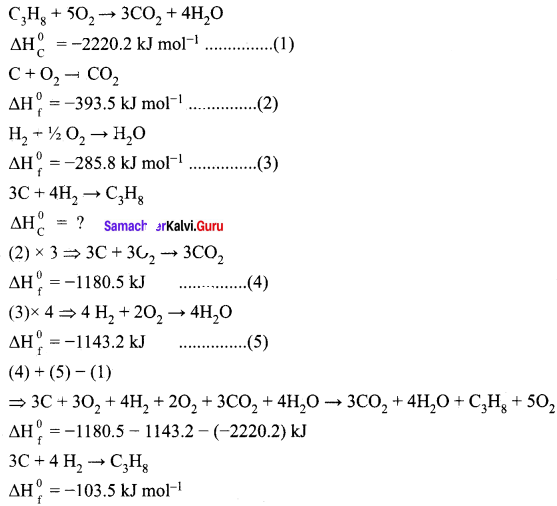
The standard heat of formation of propane is ∆Hf0(C3H8) = -103.5 kJ mol-1.
Question 59.
You are given normal boiling points and standard enthalpies of vaporization. Calculate the entropy of vaporization of liquids listed below.

Answer:
For ethanol:
Given:
Tb = 78.4°C = (78.4 + 273) = 351.4 K
∆Hv(ethanol) = + 42.4 kJ mol-1
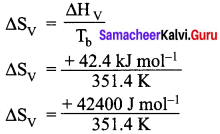
∆Hv = + 91.76 J K-1 mol-1
For Toluene:
Given:
Tb = 110.6°C = (110.6 + 273) = 383.6 K
∆SV (toluene) = + 35.2 KJ mol-1

∆SV = + 91.76 J KJ mol-1
Question 60.
For the reaction Ag2O(s) → 2Ag(s) + ½ O2(g): ∆H = 30.56 kJ mol-1 and ∆S = 6.66 JK-1 mol-1 (at 1 atm). Calculate the temperature at which AG is equal to zero. Also predict the direction of the reaction (i) at this temperature and (ii) below this temperature.
Answer:
Given,
∆H = 30.56 kJ mol-1
∆H = 30560 J mol-1
∆S = 6.66 x 10-3 kJ K-1 mol-1
T = ? at which ∆G = 0
∆G = ∆H – T∆S
0 = ∆H – T∆S
T = \(\frac {∆H}{∆S}\)
![]()
T = 4589K
(i) At 4589K ; ∆G = 0, the reaction is in equilibrium.
(ii) At temperature below 4598 K, ∆H > T ∆ S
∆G = ∆H – T∆S > 0, the reaction in the forward direction, is non-spontaneous. In other words the reaction occurs in the backward direction.
Question 61.
What is the equilibrium constant Keq for the following reaction at 400K.
2NOCl(g) ⇌ 2NO(g) + Cl2(g) given that AH° = 77.2 kJ mol-1 and ∆S° = 122 JK-1 mol-1
Answer:
Given,
T = 400 K ; ∆H° = 77.2 kJ mol-1 = 77200 J mol-1;
∆S° = 122 JK-1 mol-1
∆G° = -2.303 RT log Keq
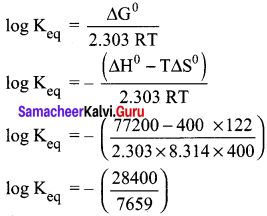
log Keq = -3.7080
Keq = anti log(-3.7080)
Keq = 1.95 x 10-4
![]()
Question 62.
Cyan-amide (NH2CN) ¡s completely burnt in excess oxygen in a bomb calorimeter, ∆U was found to be -742.4 kJ mol-1 calculate the enthalpy change of the reaction at 298K.
NH2CN(s) + 3/2 O2(g) → N2(g) + CO2(g) + H2O(l) ∆H = ?
Answer:
Given
T = 298 K;
∆U = -742.4 kJ mol-1
∆H =?
∆H = ∆U + ∆n(g)RT
∆H = ∆U + (np – nr)RT
∆H = 742.4 + 2 – \(\frac{3}{2}\) × 8.314 × 10-3 × 298
= -742.4 + (0.5 × 8.314 ×10-3 × 298)
= -742.4 + 1.24
= -741.16 kJ mol-1
Question 63.
Calculate the enthalpy of hydrogenation of ethylene from the following data. Bond energies of C H, C – C, C = C and H – H are 414, 347, 618 and 435 kJ mol-1.
Answer:
Given,
EC-H = 414 kJ mol-1
EC-H = 347 kJ mol-1
EC-H = 618 kJ mol-1
EH-H = 435 kJ mol-1
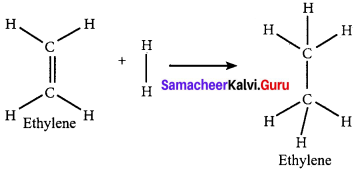
∆Hr = ∑(Bond energy)r – ∑(Bond energy)P
∆Hr = (EC=C + 4EC-H + EH-H) – (EC-C + 6EC-H)
∆Hr = (618 + (4 x 414) + 435) – (347 + (6 x 414))
∆Hr = 2709 – 2831
∆Hr = -122 KJ mol-1
Question 64.
Calculate the lattice enegry of CaCl2 from the given data
Ca(s) + Cl2(g) → CaCl2(s) ∆Hf0 = -795 KJ mol-1
Atomisation : Ca(s) → Ca(g) ∆H1° = + 121 KJ mol-1
Ionization : Ca(g) → Ca2+(g) + 2e– ∆H2° = + 242.8 KJ mol-1
Dissociation : Cl2(g) → 2 Cl(g) ∆H3° = +242.8 KJ mol-1
Electron affinity : Cl(g) + e– → Cl–(g) ∆H3° = -355 KJ mol-1
Answer:
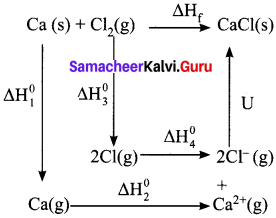
∆Hf = ∆H1 + ∆H2 + ∆H3 + 2∆H4 + u
-795 = 121 + 2422 + 242.8 + (2 x—355) + u
-795 = 2785.8 – 710 + u
-795 = 2075.8 + u
u = -795 – 2075.8
u = -2870.8 KJ mol-1
Question 65.
Calculate the enthalpy change for the reaction Fe2O3 + 3CO → 2Fe + 3CO2 from the following data.
2Fe + \(\frac{3}{2}\) O2 → Fe2O3; ∆H = -741 kJ
C + \(\frac{1}{2}\) O2 → CO; ∆H = -137 KJ
C + O2 → CO2 ∆H = -394.5 KJ
Answer:
Given,
∆Hf (Fe2O3) = -741 kJ mol-1
∆Hf(CO) = -137 kJ mol-1
∆Hf(CO2) = -394.5 kJ mol-1
Fe2O3 + 3CO → 2Fe + 3CO2 ∆Hr = ?
∆Hr = ∑(∆Hf)products – ∑(∆Hf)reactants
∆Hr = [2 ∆Hf(Fe) + 3 ∆Hf(CO2)] – [∆Hf(Fe2O3) + 3∆Hf(CO)]
∆Hr = [- 1183.5 ] – [-1152]
∆Hr = – 1183.5 + 1152
∆Hr = -31.5 KJ mol-1
Question 66.
When 1-pentyne (A) is treated with 4N alcoholic KOH at 175°C, it is converted slowly into an equilibrium mixture of 13% 1-pentyne(A), 95.2% 2-pentyne(B) and 3.5% of 1,2 pentadiene (C) the equilibrium was maintained at 175°C, calculate AG° for the following equilibria.
B ⇌ A ∆G1° = ?
B ⇌ C ∆G2° = ?
Answer:
Given
T = 175°
C = 175 + 273 = 448 K
Concentration of 1-pentyne [A] = 1.3%
Concentration of 2-pentyne [B] = 95.2%
Concentration of 1, 2-pentadiene [C] = 3.5%
At equilibrium
B ⇌ A
95.2% 1.3% ⇒
B ⇌ C
95.2% 3.5% ⇒
K2 = \(\frac{3.5}{95.2}\) = 0.0367
⇒ ∆G°1 = -2.303 RTlogK
∆G°1 = – 2.303 × 8.314 × 448 × log 0.0136
∆G°1 = +16010 J
∆G°1 = +16 kJ
⇒ ∆G°2 = – 2.303 RT log K2
∆ G°2 = -2.303 × 8.314 × 448 × log 0.0367
∆ G°2 = +12312J
∆G°2 = +12.312 kJ
![]()
Question 67.
At 33K. N2H4 is fifty percent dissociated. Calculate the standard free energy change at this temperature and at one atmosphere.
Answer:
T = 33K
N2O4 ⇌ 2NO2
Initial concentration 100%
Concentration dissociated 50%
Concentration remaining at equilibrium 50% – 100%
Keq = \(\frac{100}{50}\) = 2
∆G° = -2.303 RT log Keq
∆G° = -2.303 x 8.31 x 33 x 1og 2
∆G° = -190.18 J mol-1
Question 68.
The standard enthaipies of formation, of SO2 and SO3 are -297, kJ. rnol-1 and -396 kJ mol-1 respectively. Calculate the standard enthalpy of reaction for the reaction:
SO2 + \(\frac{1}{2}\) O2 → SO3
Answer:
Given
∆H°f(SO2) = – 297 kJ mol-1
∆H°f(SO3) = – 396 kJ mol-1
SO2 + 12O2 → SO3;
∆H°r =?
∆H°r = (∆H°f)compound – Σ( ∆Hf)elements
∆H°r =∆H°r(SO3) – ∆H°f
∆H°r = 396 kJ mol-1– (- 297 kJ mol-1 + 0)
∆H°r = – 396 kJ mol-1 + 297
∆H°r = -99 kJ mol-1
Question 69.
For the reaction at 298 K : 2A + B → C
∆H = 400 J mol-1 ∆S = 0.2 JK-1 mol-1
Determine the temperature at which the reaction would be spontaneous.
Answer:
Given,
T = 298K
∆H = 400 J mol-1
∆S = 0.2 J K-1 mol-1
∆G = ∆H – ThS
if T = 2000K
∆G = 400 – (0.2 x 2000) = 0
if T > 2000 K
∆G will be negative.
The reaction would be spontaneous only beyond 2000 K.
Question 70.
Find out the Value ofequilibrium constant for the following reaction at 298K,
2 NH3(g) + CO2(g) ⇌ NH2CONH2(aq) + H2O(l)
Standard Gibbs energy change, AGr° at the given temperature is – 13.6 kJ mol-1.
Answer:
Given,
T = 298 K
∆Gr° = – 13.6 kJ mol-1
= – 13600 J mol-1
∆G° = – 2.303 RT log Keq
log Keq = \(\frac{-∆G°}{2.303 RT}\)
log Keq ![]()
log Keq = 2.38
Keq = anti log(2.38)
Keq = 239.88.
Question 71.
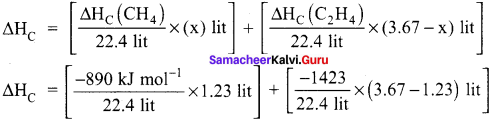
A gas mixture of 3.67 lit of ethylene and methane on complete combustion at 25°C and at I atm pressure produces 6.11 lit of carbon dioxide. Find out the amount of heat evolved in kJ, during this combustion. (∆HC(CH4) = – 890 kJ mol-1 and (∆HC(C2H4)= -1423 kJ mol-1.
Answer:
Given,
∆HC (CH4) = – 890 kJ mol-1
∆HC (C2H4) = -1423 kJ mol-1
Let the mixture contain x lit of CH4 and (3.67 – x) lit of ethylene.

Volume of carbon dioxide formed x + 2 (3.67 – x) 6.11 lit
x + 7.34 – 2x = 6.11
x = 1.23 lit
Given mixture contains 1.23 lit of methane and 2.44 lit of ethylene, hence

∆HC = [-48.87 kJ mol-1] + [-155 kJ mol-1]
∆HC = -203.87 kJ mol-1
In-Text Questions – Evaluate Yourself
Question 1.
Calculate AH for the reaction CO2(g) + H2(g) → CO(g) + H2O(g) given that ∆Hr° for CO2(g), CO(g) and H2O(g) are – 393.5, – 111.31 and – 242 kJ mol-1 respectively.
Given,
∆Hf° CO2 = -393.5 kJ mol-1
∆Hf° CO = -111.31 kJ mol-1
∆Hf° (H2O) = – 242 kJ mol-1
CO2(g) + H2(g) → CO(g) + H2O(g)
∆Hr° = ?
∆Hr° = ∑(∆Hf°)products – ∑(∆Hf°)products
∆Hr° = [∆Hf° (CO) + ∆Hf° (H2O)] – [∆Hf° (CO2) + ∆Hr° (H2)]
∆Hr° = [- 111.31 + (-242)] – [- 393.5 +(0)]
∆Hr° = [- 353.31] + 3935
∆Hr° = 40. 19
∆Hr° = 40.19 KJ mol-1
![]()
Question 2.
Calculate the amount of heat necessary to raise 180 g of water from 25°C to 100°C. Molar heat capacity of water is 75.3 J mol-1 K-1
Answer:
Given:
Number of moles of water n = \(\frac{180 \mathrm{g}}{18 \mathrm{g} \mathrm{mol}^{-1}}\) = 10 mol molar heat capacity of water
Cp = 75.3 J K-1 mol-1
T2 = 100°C = 373K
T1 = 25°C = 298K
∆H = ?
∆H = nCp(T2 – T1)
∆H = 10 mol x 75.3 J mol-1 K-1 x (373 – 298) K
∆H = 56475 J
∆H = 56.475 kJ
Question 3.
From the following data at constant volume for combustion of benzene, calculate the heat of this reaction at constant pressure conditions.
C6H6(l) + \(\frac {7}{2}\) O2(g) → 6 CO6(g)+ 3 H2O(l)
∆U at 25°C = -3268.12 kJ
Answer:
Given,
T = 25°C = 298 K;
∆U = -3268.12 KJ mol-1
∆H = ?
∆H = ∆U + ∆ng RT
∆H = ∆U + (np – nr)RT
∆H = 3268.12 + [6 – \(\frac{7}{2}\) x 8.314 x 10-3 x 298
∆U = -3268.12 + (2.5 x 8.314 x 10-3 x 298)
∆U = – 3268.12+6.L9
∆U = -3261.93 kJ mol-1
Question 4.
When a mole of magnesium bromide is prepared from 1 mole of magnesium and 1 mole of liquid bromine, 524 kJ of energy is released. The heat of sublimation of Mg metal is 148 kJ mol-1. The heat of dissociation of bromine gas into atoms is 193 kJ mol-1. The heat of vapourisation of liquid bromine is 31 kJ mol-1. The ionisation energy of magnesium is 2187 kJ mol-1 and the electron affinity of bromine is – 662 kJ mol-1. Calculate the lattice energy of magnesium bromide.
Answer:
Given,
Mg(s) + Br2(l) MgBr2(s) – ∆Hf° = – 524 KJ mol-1
Sublimation:
Mg(s) → Mg(g) – ∆Hf° = +148 KJ mol-1
Ionisation:
Mg(g) → Mg2+(g) + 2e– 2187 – ∆Hf° = 2187 KJ mol-1
Vapourisation:
Br2(l) → Br2(g) – ∆Hf° = + 31 KJ mol-1
Dissociation:
Br2(g) → 2Br(g) – ∆Hf = + 193 KJ mol-1
Electron affinity:
Br(g) + e – → Br– (g) – ∆Hf = -331 KJ mol-1
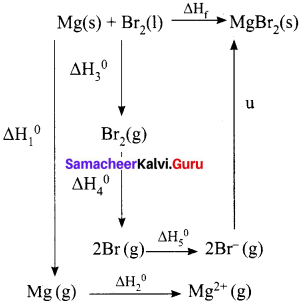
∆Hf = ∆H1 + ∆H2 + ∆H3 + ∆H4 + 2AH5 + u
-524 = 148 + 2187 + 31 + 193 + (2 x – 331) + u
-524 = 1897 + u
u = -524 -1897
u = – 2421 kJ mol-1
Question 5.
An engine operating between 127°C and 47°C takes some specified amount of heat from a high-temperature reservoir. Assuming that there are no frictional losses, calculate the percentage efficiency of an engine.
Answer:
Given,
T1 = 127°C = 127 + 273 = 400 K
T2 = 47°C = 47 + 273 = 320 K
% efficiency η = ?
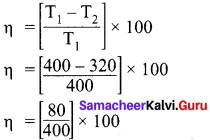
η = 20%
![]()
Question 6.
Urea on hydrolysis produces ammonia and carbon dioxide. The standard entropies of urea, H2O. CO2, NH3 are 173.8, 70, 213.5 and 192.5 J mole-1K-1 respectively. Calculate the entropy change for this reaction.
Answer:
Given,
S°(urea) = 173.8 J mol-1K-1
S° (H2O) = 70 J mol-1 K-1
S° (CO2) = 213.5 J mol-1 K-1
S° (NH3) = 192.5 J mol-1 K-1
NH2 – CO – NH2 + H2O → 2NH3 + CO2
∆Sr° = ∑(S°)product – ∑(S°)reactants
∆Sr° = [2 S°(NH3) + S°(CO2)] — [S°(urea) + S°(H2O)]
∆Sr° = [2 x 192.5 + 213.5] – [173.8 + 70]
∆Sr° = [598.5] – [243.8]
∆Sr° = 354.7 J mol-1 K-1
Question 7.
Calculate the entropy change when I mole of ethanol is evaporated at 351 K. The molar heat of vapourisation of ethanol is 39.84 kJ mol-1
Answer:
Given,
Tb = 351 K
∆Hvap = 39840 J mol-1
∆HV = ?
∆HV = \(\frac{\Delta \mathrm{H}_{\mathrm{vap}}}{\mathrm{T}_{\mathrm{b}}}\)
∆HV = 113.5 JK-1mol-1
Question 8.
For a chemical reaction, the values of ∆H and ∆S at 300 K are – 10 kJ mol-1 and -20 J mol-1 respectively. What is the value of AG of the reaction? Calculate the ∆G of a reaction at,600K assuming ∆H and AS values are constant. Predict the nature of the reaction.
Answer:
Given,
∆H =- 10 kJ mol = -10000 J mol-1
∆S = -20 JK-1 mol-1
T = 300 K
∆G = ?
∆G = ∆H – T∆S
∆G = – lo kJ mol-1 -300 K x (-20 x 10-3)kJ K-1 mol-1
∆G = (-10 + 6) kJ mol-1
∆G =-4 kJ mol-1
At 600 K,
∆G = – 10 kJ mol-1 -600 K x (-20 x 10-3)kJ K-1 mol-1
∆G =(-10+12) kJ mol-1
∆G = +2 kJ mol-1
The value of ∆G is negative at 300K and the reaction is spontaneous, but at 600K the value ∆G becomes positive and the reaction is non-spontaneous.
In-Text Example Problems
Question 1.
A gas contained in a cylinder fitted with a frictionless piston expands against a constant external pressure of 1 atm from a volume of 5 litres to a volume of 10 litres. In doing solt absorbs 400 J of thermal energy from its surroundings. Determine the change in internal energy of system.
Answer:
Given data q = 400 J; V1 = 5L; V2 = 10L
Au = q – w (heat is given to the system (±q); work is done by the system(-w)
Au = q – PdV
= 400 J – 1 atm (10 – 5)L
= 400 J – 5 atm L [∴ 1L atm = 101.33 J]
= 400 J – 5 x 101.33 J
= 4003 – 506.65 J
= – 106,65 J
Question 2.
The standard enthalpies of formation of C2H5OH(l), CO2(g) and H2O(l) are – 277, -393.5 and -285.5 kJ mol-1 respectively. Calculate the standard enthalpy change for the reaction. C2H5OH(l) + 3O2(g) → 2CO2(g) + 3H2O(l). The enthalpy of formation of O2(g) in the standard state is zero by definition.
Answer:
The standard enthalpy change for the combustion of ethanol can be calculated from the strndard enthalpies of formation of C2H5OH(l), CO2(g) and H2O(l). The enthalpies of formation are – 277, – 393.5 and – 285.5 kJ mol-1 respectively.
C2H5OH(l) + 3O2(g) → 2CO2(g) + 3H2O(l).
= [-787 – 856.5] – [-277]
= -1643.5 + 277
∆Hr° = -1366.5 KJ.
Question 3.
Calculate the value of AU and AH on heating 128 g of oxygen from 0°C to 100°C. C. and C, on an average are 21 and 29 J mol-1 K-1. (The difference is 8 J mol-1 K-1 which is approximately equal to R)
Answer:
We know
∆U = n CV (T2 – T1)
∆H = n CP (T2 – T1)
Here n = \(\frac {128}{32}\)4 moles;
T2 = 100°C = 373 K
T1 = O°C = 273 K
∆U = n CV(T2 – T1)
∆U = 4 x 21 x (373 – 273)
∆U = 8400 J
∆U = 8.4 kJ
∆H = nCP (T2 – T1 )
∆H = 4 x 29 x (373 – 273)
∆H = 11600 J
∆H = 11.6 KJ.
![]()
Question 4.
Calculate the enthalpy of combustion of ethylene at 300 K at constant pressure, If Its heat of combustion at constant volume (∆U) is – 1406 KJ.
Answer:
The complete ethylene combustion reaction can be written as,
C2H4(g) + 3O2(g) → 2CO2(g) + 2H2O(l)
∆U = -1406 kJ
∆n = np(g) – nr(g)
∆n = 2 – 4 = -2
∆H = U + RT ∆n(g)
∆H = -1406 + (8.314 x 10-3 x 300 x (-2))
∆H = – 1410.9 kJ
Question 5.
Calculate the standard enthalpy of formation ∆H°f of CH4 from the values of enthalpy of combustion for H2, C (graphite) and CH4 which are -285.8, -393.5, and -890.4 KJ mol-1 respectively.
Answer:
Let us interpret the information about enthalpy of formation by writing out the equations. It is important to note that the standard enthalpy of formation of pure elemental gases and elements is assumed to be zero under standard conditions. The thermochemical equation for the formation of methane from its constituent elements is,
C(graphite) + 2H2(g) → CH4(g)
∆Hf0 = X kJ mol-1 …………(i)
Thermo chemical equations for the combustion of given substances are,
2H2(g) + \(\frac {1}{2}\) O2 → H2O(l)
∆H0 = – 285.8 KJ mol-1 …………..(ii)
C(graphite) + O2 → CO2
∆H0 = -393.5 KJ mol-1 …………….(iii)
CH4(g) + 2O2 → CO2(g) + 2H2O(l)
∆H0 = -890.4 KJ mol-1 ……………(iv)
Since methane is in the product side of the required equation (i), we have to reverse the equation (iv)
CO4(g) + 2H2O(l) → CH4(g) + 2O2
∆H° = + 890.4 kJ mol-1 …………….(v)
In order to get equation (i) from the remaining, (i) = [(ii) x 2] + (iii) + (v)
X = [(-285.8) x 2] + [-393.5] + [+ 890.4] = -74.7kJ
Hence, the amount of energy required for the formation of I mole of methane is -74.7 kJ The heat of formation methane -74.7 kJ mol-1
Question 6.
Enthalpy for the oxidation of graphite to CO2 and CO to CO2 can easily be measured. For these conversions, the heat of combustion values are -393.5 kJ and -283.5 kJ respectively.
Answer:
From these data the enthalpy of combustion of graphite to CO can be calculated by applying Hess’s law. The reactions involved in this process can be expressed as follows:
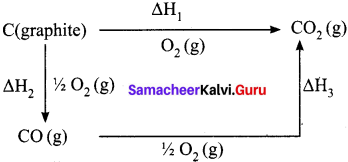
According to Hess law,
∆H1 = ∆H2 + ∆H3
-393.5 kJ = X – 283.5 kJ
X = – 110.5 kJ
Question 7.
Calcu late the lattice energy of sodium chloride using Born-Haber cycle.
Answer:
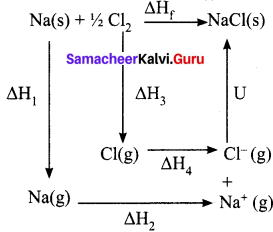
∆Hf = heat of formation of sodium chloride = 411.3 kJ mol-1
∆H1 = heat of sublimation of Na(s) = 108.7 kJ mol-1
∆H2 = ionisation energy of Na(s) = 495 kJ mol-1
∆H3 = dissociation energy of Cl2(s) = 244 kJ mol-1
∆H4 = Electron affinity of Cl(s) = – 349 kJ mol-1
U = lattice energy of NaCl
∆Hf = ∆H1 + ∆H2 + ½ ∆H3 + ∆H4 + U
∴U = (∆Hf) – (∆H1 +∆H2 + ½ ∆H3 + ∆H4)
=>U = (-411.3) – (108.7 + 495 + 122 – 349)
U = (-41 1.3) – (376.7)
∴U = -788 kJ mol-1
This negative sign in lattice energy indicates that the energy is released when sodium is the time from its constituent gaseous ions Na+ and Cl–
![]()
Question 8.
If an automobile engine burns petrol at a temperature of 8 16°C and if the surrounding temperature is 21°C, calculate its maximum possible efficiency.
Answer:
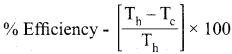
Here
Th = 816 + 273 = 1098 K
Tc = 21 + 273 = 294 K
Samacheer Kalvi 11th Chemistry Solutions Chapter 7 Thermodynamics
% Efficiency = 73%.
Question 9.
Calculate the standard entropy change for the following reaction (∆Hf°), given the standard entropies of COf (g), C(s), O2(g) as 213.6, 5.740 and 205 JK-1 respectively.
C(g) + O2(g) → CO2(g)
∆Sr° = ∑ Sproducts° – Sreactants°‘
∆Sr° = {SCO2°°} – {Sc° + SO2°°}
∆Sr° = 213.6 – [5.74 + 205]
∆Sr° = 213.6 – [210.74]
∆Sr° = 2.86 JK-1.
Question 10.
Calculate the entropy change during the melting of one mole of ice into water at 0°C and I atm pressure. Enthalpy of fusion of ice is 6008 J mol-1.
Answer:
Given,
∆Sfusion = 6008 J mol-1
Tf = 0°C = 273 K
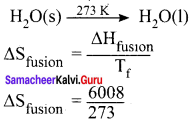
∆Sfusion = 22.007 JK-1 mol-1
Question 11.
Show that the reaction CO +½ O2 → CO2 at 300 K is spontaneous. The standard Gibbs free energies of formation of CO2 and CO are -394.4 and -137.2 kJ mole respectively.
Answer:
CO + ½ O2 → CO2
∆G(reaction)° = ∑Gf(products)° – ∑Gf(reactants)°
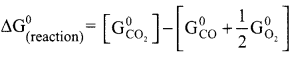
∆G(reaction)° = -394.4 + [137.2 + 0]
∆G(reaction)° = -257.2 KJ mol-1
∆G(reaction)° of a reaction at a given temperature is negative hence the reaction is spontaneous.
Question 12.
Calculate G° for conversion of oxygen to ozone 3/2 O2 ⇌ O3(g) at 298 K, if Kp for this conversion is 2.47 x 10-29 in standard pressure units.
Answer:
∆G° = -2.303 RT log Kp
Where
R = 8.314 JK-1mol-1
K = 2.47 x 10-29
T = 298 K
∆G° = – 2.303(8.314)(298) log (2.47 x 10-29)
∆G°= 16300 J mol-1
∆G° = 16.3 KJ mol-1
Additional:
Question 1.
Calculate the maximum % efficiency of thermal engine operating between 110°C and 25°C.
Answer:
% Efficiency = \(\left[\frac{\mathrm{T}_{1}-\mathrm{T}_{2}}{\mathrm{T}_{1}}\right]\) x 100
T1 = 110°C + 273 = 383 K.
T2 = 25°C – 273 = 298 K.
% Efficiency = \(\left[\frac{383 – 298}{383}\right]\) x 100
% Efficiency = \(\left[\frac{85 × 100}{383}\right]\) = \(\left[\frac{8500}{383}\right]\) % Efficiency = 22.2%
Question 2.
Calculate the entropy change in the system. and in the surroundings and the total entropy change in the universe when during a process 75 J of heat flow out of the system at 55°C to the surrounding at 20°C.
Answer:
Heat flow (q) = 75 J
Entropy change = ∆S = ?
Temperature of the system = 55°C + 273 = 328 K
Temperature of the surroundings = 20°C + 273 = 293 K

= 0.2286 + 0.2559 = ∆Suniverse = 0.4845 JK-1
Question 3.
1 mole of an ideal gas is maintained at 4.1 atm and at a certain temperature absorbs 3710 J heat and expands to 2 litres. Calculate the entropy change in expansion process.
Answer:
Pressure of an ideal gas Pi = 4.1 atm.
Expansion in volume = ∆V = 2 litres
Heat absorbed = q = 3710 J
Entropy change = ∆S = ?
For an ideal gas PV = RT for one mole.
T = \(\frac {PV}{R}\) = \(\frac {4.1 x 2}{0.0830}\) = 100°C
T = 100 + 273 = 373 K.
∆S = \(\frac{q}{\mathrm{T}_{(\mathrm{K})}}\) = \(\frac{3710}{373}\)
Entropy change = 9.946 JK-1.
Question 4.
Calculate the entropy change of a process H2O(l) → H2O(g) at 373K. Enthalpy of vaporization of water is 40850 J Mole-1.
Answer:
H2O(l) → H2O(g)
Temperature T = 373 K
Enthalpy of vapourisation of water = ∆Vvap = 40580 J mol-1
∆S = entropy change 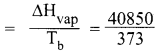
∆S(entropy change) = 109.51 J mol-1 K-1
Question 5.
30.4 KJ is required to melt one mole of sodium chloride. The entropy change during melting is 28.4 JK-1 mol-1 Calculate the melting point of sodium chloride.
Answer:
Heat required for I mole of NaCl for melting (q) = 30.4 K J
= 30.4 x 1000 J
∆S – entropy change = 28.4 J K-1 mol-1
Melting point = Tm = ?
∆S = \(\frac{q}{\Gamma_{m}}\)
∴ Tm = \(\frac{q}{∆S}\)
Tm = \(\frac{30.4 x 1000}{28.4}\) = 10704 K
Melting point of NaCl = 1070.4 K.
![]()
Question 6.
Calculate the standard heat of formation of propane, if its heat of combustion is 0-2220.2 KJ mol-1 [he heats of formation of CO2(g) and H2(g)O(l) are -393.5 and -285.8 kJ mol-1 respectively.
Solution:
Standard heat of formation of propane,
3C(g) + 4H2(g) → C3H8(g) ∆Hf° = ?
Data given:
C3H8(g) + 5O2(g) → 3CO2 + 4H2O(l) ∆H = -2220.2 KJ mol-1
C(s) + O2(g) → CO2(g) ∆H = -393.5 KJ mol-1
H2(g)(g) + ½ O2(g) → H2 O(l) ∆H = -285.8 KJ mol-1
According to Hes&s law, equation
Equation (1) is reversed.
Equation (2) is x 3
Equation (3) is x 4
Then add all the equations.
3CO2(g) + 4H2O(l) → C3H8(g) + 5O2(g) ∆H1 = + 2220.2 KJ mol-1
3C(s) + 3O2(g) → 3CO22(g) ∆H2 = -1180.5 KJ mol-1
4H2(g) + 2O2(g) → 4H2O(l) ∆H3 = -1143.2 KJ mol-1
3C(S) + 4H2(g) → C3H8(g) ∆Hf° = -103.5 KJ mol-1
Standard enthalpy of formation of propane ∆Hf° = -103.5 K.J mol-1
Question 7.
The boiling point of water at a pressure of 50 atm is 265°C. Compare the theoretical efficiencies of a steam engine operating between the boiling point of water at
1. 1 atm pressure
2. 50 atm pressure, assuming the temperature of the sink to be 35°C in each case.
Answer:
Boiling point of water at 50 atm pressure (Tb) = 265°C = 265 + 273 = 538K
1. Boiling point of water at 1 atm pressure (Tb) = 100°C = 100 + 273 = 373K
% Efficiency of steam engine = \(\left[\frac{\mathrm{T}_{1}-\mathrm{T}_{2}}{\mathrm{T}_{1}}\right]\) x 100 = \(\left[\frac{538-373}{538}\right]\) x 100 = 0.3066 x 100 = 30.66%
2. BoiLing point of water at 50 atm pressure (Tb) = 35°C = 35 + 273 = 328 K
% Efficiency of steam engine = \(\left[\frac{\mathrm{T}_{1}-\mathrm{T}_{2}}{\mathrm{T}_{1}}\right]\) x 100 \(\left[\frac{538-328}{538}\right]\) x 100 = \(\left[\frac{210 x 100}{538}\right]\) = 39.03 %
Question 8.
The standard enthalpies of formation of SO2 and SO3 are -297 kJ mol-1 and -396 kJ mol-1 respectively. Calculate the standard enthalpy of reaction for the reaction: SO2 + ½ O2 → 4 SO3
Solution:
Data are given,
(1) ⇒ S + O2 → SO2 ∆Hf° = -297 KJ mol-1
(2) ⇒ S + 1½O2 → SO3 ∆Hf° = -396 KJ mol-1
SO2 + ½ O2 →SO3 ∆Hr = ?
Equation (1) is reversed and added with equestion (2)

Question 9.
For the reaction at 298 K : 2A + B → C
∆H = 400 KJ mol-1: ∆S = 0.2 JK-1 mol-1
Determine the temperature at which the reaction would be spontaneous.
Solution:
Data given,
2A + B → C at 298 K
∆H = 400 KJ mol-1
∆S = 0.2 JK-1 mol-1
T = 298 K
[∆G = ∆H – T∆S]
if ∆G = 0
∆H – T∆S = 0
∆S = \(\frac {∆H}{T}\)
For ∆G = 0, ∆S = \(\frac {∆H}{T}\) = \(\frac {400}{0.2}\) = \(\frac {4000}{2}\) = 2000K
∴ T = 2000K
At 2000 K. the reaction is in equilibrium. So. above 2000 K, the reaction will be spontaneous.
Question 10.
Calculate the heat of glucose and its calorific value
1. C(graphite) + O2(g) → CO2(g) ∆H = -395 KJ
2. H2(g) + hO2 → H2O(l) ; ∆H = -269.4 KJ
3. C + 6H2(g) + 3O2(g) → C6H12O6(S) ∆H = -1169.8 KJ
Solution:
The calorific value of glucose ∆HC =?
![]()
Data given are.
1. C(graphite) + O2(g) → CO2(g) ∆H = -395 KJ ………….(1)
2. H2(g) + 1/2 O2 → H2O(l) ∆HC ∆H = -269. 4 KJ ………….(2)
3. C + 6H2(g) + 3O2(g) → C6H12O6(S) ∆H = – 1169.8 KJ …………(3)
Equation (1) x 6 6C + 6O2 → 6CO2 ∆H = – 2370 KJ
Equation (2) x 6 6H2 + 3O2 → 6H2O ∆H = – 1616.4 KJ
Equation (3) is reversed,
C6H12O6 → 6C + 6H2 +3O2 ∆H = + 1169.8 KJ
Add all equations,
C6H12O6 + 6O2 → 6CO2 + 6H2O
∆H = – 2370 – 1616.4 + 1169.8
∆H = – 3986.4 + 1169.8
∆H = – 2816.6 KJ
Calorific value of C6H12O6 = -2816.6 KJ mol-1
![]()
Question 11.
Calculate the entropy change when 1 mole of ethanol is evaporated at 351 K. The molar heat of vapourisation of ethanol is 39.84 kJ mol-1
Answer:
Given,
∆Hvap = 39840 J mol-1
∆Hv = \(\frac{\Delta \mathrm{H}_{\mathrm{vap}}}{\mathrm{T}_{b}}\)
Tb = 351 K
∆Hv = \(\frac{39840}{351}\)
∆Hv = 113.5 J k-1 mol-1
Question 12.
Calculate the entropy change of a process possessing ∆Ht = 2090 J mole-1
Answer:
Given,
Sn(α 13°C) – Sn(β 13°C)
∆Ht = 2090 J mol-1
∆St = \(\frac{\Delta \mathrm{H}_{t}}{\mathrm{T}_{t}}\)
∆St = \(\frac{2090}{286}\)
∆St = 7.307 J K-1 mol-1
Question 13.
Calculate the standard enthalpy of formation of CH3OH(l) from the following data:
(i) CH3OH(l) + 3/2O2(g) → CO2(g) + 2H3O(l) ∆r\({ H }^{ \ominus }\) = -726 kJ mol-1
(ii) C(S) + O2(g) → CO2(g); ∆C \({ H }^{ \ominus }\) = – 393 kJ mol-1
(iii) H2(g) + ½ O2(g) → H2O(l) ∆f \({ H }^{ \ominus }\) = – 286 kJ mol-1
Answer:
The equation we aim at;
C(S) + 2H2(g) + O2(g) → CH3OH(l) ∆f \({ H }^{ \ominus }\) = ± ? ………..(iv)
Multiply equation (iii) by 2 and add to equation (ii)
C(S) + 2H2(g) + 2O2(g) → CO2(g) + 2H2O(l) ∆H = – (393 + 522) = – 965 kJ mol-1
Subtract equation (iv) from equation (i)
CH3OH(l) + 3/2 O2(g) → CO2(g) + 2H2O(l) ∆H = -726 kJ mol-1
Subtract:
C(S) + 2H2(g) + ½ O2(g) → CH3OH(l) ∆f\({ H }^{ \ominus }\)= -239 kJ mol-1
Question 14.
The equilibrium constant for the reaction is 10. Calculate the value of ∆G-;
Given R = 8.3 14 JK-1 mol-1; T = 300 K.
Answer:
∆Ge = -RT in K = -2.303 RT log K
R = 8.314 JK-1 mol-1; T = 300 K; K = 10
∆Ge = – 2.303 x 8.314 JK-1 mol-1 x (300 K) x log 10
= -5527 J mol-1 = -5.527 kJ mol-1
Question 15.
Calculate the entropy change in surroundings when 1 mol-1 of H2O(l) is formed under standard conditions. Given ∆H = – 286 kJ mol-1
Answer:
qrev = (-Δf\({ H }^{ \ominus }\)) = -286 KJ mol = 286000 J mol
![]()
Question 16.
The enthalpy of formation of methane at constant pressure and 300 K is – 78.84 kJ.What will be the enthalpy of formation at constant volume?
Answer:
The equation representing the enthalpy of formation of methane is:
C(S) + 2H2(g) – CH2(g);
∆H = – 78.84 kJ
∆U = 78.84 kJ;
∆ng = 1 – 2 = -1 mol
R = 8.314 x 10-13 KJ K-1 mol-1; T = 300 K.
According to the relation,
∆H = ∆U + ∆ng RT – 78.84 kJ
∆U = ∆H – ∆ng RT
∆U = (- 78.84 kJ) – (1 mol) x (8.314 x 10-3 KJ K-1 mol-1 ) x 300K.
= – 78.84 – 2.49 = -8.314 KJ.
![]()
Question 17.
Calculate ∆rGe for conversion of oxygen to ozone 3/2 O2(g) → O3(g) at 298 Kp If for this conversion is 2.47 x 10-29.
Solution:
We know
∆r\({ G }^{ \ominus }\) = -2.303 RT log Kp
R = 8.314 JK-1 mol-1
∆r\({ G }^{ \ominus }\)= -2.303 (8.314 J K-1 mol-1) x (298 K) (log 2.47 x 10-29)
= 163000 J mol-1 = 163 mol-1
Question 18.
(a) Under what condition, the heat evolved or absorbed in a reaction ¡s equal to its free energy change?
(b) Calculate the entropy change for the following reversible process.
H2O(s) ⇌ H2O(l) ∆fusH is 6 kJ mol-1
(a) ∆G = ∆H – T∆S
When the reaction is carried out at 0°K
or ∆S = 0
∆G = ∆H
H2O(s) ⇌ H2O(l)
∆fusH = 6 kJ mol-1 = 6000Jmol-1
∆fusH = 6 kJ mol-1
6000 J mol-1
Samacheer Kalvi 11th Chemistry Thermodynamics Additional Questions Solved
I. Choose the correct answer from the following:
Question 1.
_______is a part of the universe which is separated from the rest of the universe by real or imaginary boundaries.
(a) Surroundings
(b) boundary
(c) system
(d) matter
Answer:
(c) system
Question 2.
if ∆G for a reaction is negative, the change is ……….
(a) spontaneous
(b) non-spontaneous
(c) reversible
(d) equilibrium
Answer:
(a) spontaneous
Question 3.
Which of the following is/are extensive properties?
1. volume
2. Surface tension
3. mass
4. internal energy
(a) 1, 2 and 4
(b) 1, 3 and 4
(c) 1 and 3
(d) 1, 2 and 3
Answer:
(b) 1, 3 and 4
Question 4.
Change in Gibbs free energy is given by
(a) ∆G = ∆H +T∆S
(b) ∆G = ∆H – T∆S
(c) ∆G = H x T∆S
(d) none of these
Answer:
(b) ∆G = ∆H – T∆S
Question 5.
For an isothermal process _______.
(a) dT = 0
(b) dV = 0
(c) dq = 0
(d) dP = 0
Answer:
(a) dT = 0
![]()
Question 6.
Calculate the entropy change during the melting of one mole of ice into water at 0°C and 1 atm pressure. Enthalpy of fusion of ice is 6008 J Mole-1.
(a) 22.007 J K-1Mole-1
(b) 22.007 J K-1 Mole-1
(c) 220.07 J K-1 Mole-1
(d) 2.2007 J K-1 Mole-1
Answer:
(a) 22.007 J K-1 Mole-1
Hint:
Enthalpy of fusion of ice 6008 J mol-1 = ∆H
∆S = \(\frac{\Delta \mathrm{H}}{\mathrm{T}_{\mathrm{m}}}\) Tm = 0°C = 273 K
![]()
∆S = \(\frac{6008}{273}\) = 22.007 J K-1 mol-1
Question 7.
Which of the following is/are path functions?
1. pressure
2. work
3. internal energy
4. Free energy
5. heat
(a) 1, 2 and 4
(b) 1, 3 and 4
(c) 2 and 5
(d) 2, 3 and 4
Answer:
(c) 2 and 5
Question 8.
The final temperature of an engine whose initial temperature is 400K and having an efficiency of 25%.
(a) 200K
(b) 400K
(c) 300K
(d) 450K
Answer:
(c) 300K
Solution:
Initial temperature = T1 = 400 K
Final temperature = T2 = ?
Efficiency = 25%
η = \(\left[\frac{\mathrm{T}_{1}-\mathrm{T}_{2}}{\mathrm{T}_{1}}\right]\) x 100
25 = \(\left[\frac{400-\mathrm{T}_{2}}{400}\right]\) x 100
\(\frac{400-T_{2}}{4}\) = 25
400 – T2 = 100
– T2 = 100 – 400
∴ -T2 = -300
T2 = 300 K
Question 9.
When solid melts there is ………
(a) an increase of entropy
(b) a decrease in entropy
(c) an increase in free energy
(d) an increase of heat of fusion
Answer:
(a) an increase of entropy
Question 10.
The unit of entropy is ………
(a) J K-1 mol-1
(b) J mol-1
(c) J K mol-1
(d) J-1 K-1
Answer:
(a) J K-1 mol-1
Question 11.
If G = 0. then the process is …………
(a) equilibrium
(b) spontaneous
(c) non-spontaneous
(d) none of these
Answer:
(a) equilibrium
Question 12.
The standard conditions for G° are ………..
(a) 1 mm Hg / 25°C
(b) 1 atm /25 K
(c) 1 attn / 298 K
(d) 1 atm / 0K
Answer:
(c) 1 atm / 298 K
![]()
Question 13.
The efficiency of engine working between 100 to 400 K
(a) 25%
(b) 75%
(c) 100%
(d) 50%
Answer:
(b) 75%
Solution:
η = \(\left[\frac{\mathrm{T}_{1}-\mathrm{T}_{2}}{\mathrm{T}_{1}}\right]\) x 100
T1 = 400K
T2 = 100 K
∴ η = \(\left[\frac{\mathrm{T}_{1}-\mathrm{T}_{2}}{\mathrm{T}_{1}}\right]\) x 100
![]()
= 75%
Question 14.
Entropy is a ………. function.
(a) state
(b) path
(c) defined
(d) undefined
Answer:
(a) state
Question 15.
An efficiency of an engine is always ………..
(a) = 0%
(b) > 100%
(c) < 100%
(d) = 100%
Answer:
(c) < 100%
Question 16.
if the system moves from ordered state to disordered state, its entropy ………..
(a) decreases
(b) increases
(c) become zero
(d) increases then decrease
Answer:
(b) increases
Question 17.
In a reversible process, the entropy of Universe is ………..
(a) greater than zero
(b) less than zero
(c) equal to zero
(d) remains constant
Answer:
(c) equal to zero
Question 18.
In which of the following entropy increases?
(a) Condensation of water vapour
(b) Liquid freezes to solid
(c) Sublimation
(d) Gas freezes to a solid
Answer:
(c) Sublimation
Question 19.
Which of the following is a state function?
(a) q
(b) ∆q
(c) w
(d) ∆S
Answer:
(d) ∆S
Question 20.
Which of the following is correct option for free expansion of an ideal gas under adiabatic condition?
(a) q = 0, ∆T ≠ 0, w = 0
(b) q ≠ 0, ∆T = 0, w = 0
(c) q = 0, ∆T = 0, w = 0
(d) q = 0, ∆T < 0, w ≠ 0
Answer:
(b) q ≠ 0, ∆T = 0, w = 0
Question 21.
Which of the following is not a state function?
(a) S
(b) H
(c) G
(d) q
Answer:
(d) q
![]()
Question 22.
The net work done by the system ………..
(a) w – P∆V
(b) w +P∆V
(c) -w + P∆V
(d) -w – P∆V
Answer:
(d) – w – P∆V
Question 23.
– ∆G is the net work done by the system except ………..
(a) electrical work
(b) expansion work
(c) chemical work
(d) photochemical work
Answer:
(b) expansion work
Question 24.
The subject matter of thermodynamics comprises
(a) energy transformations in a system
(b) mass changes in molecular reactions
(c) total energy of system
(d) rates of chemical reactions
Answer:
(a) energy transformations in a system
Question 25.
In a reversible process ∆Ssys + ∆Ssurr is ………..
(a) >0
(b)<0
(c) ≥0
(d) = 0
Answer:
(d) = 0
Question 26.
Which of the following does not result in an increase in the entropy?
(a) Crystallization of sucrose from solution
(b) Rusting of Iron
(c) Conversion of ice to water
(d) Vaporization of camphor
Answer:
Crystallization of sucrose from solution
Question 27.
The standard free energy change (∆G°) is related to equilibrium constant (K) as …………
(a) ∆G° = – 1303 RT in K
(b) ∆G° = 2.303 RT log K
(c) ∆G° = RT in K
(d) ∆G° = -2.303 RT log K
Answer:
(d) ∆G° = -2.303 RT log K
![]()
Question 28.
enropy change involved in the conversion of I mole of liquid water at 373K to vapour at the same temperature will be (∆Hvap = 2.257 kJ g-1)
(a) 0.119 kJ
(b) 0.109 kJ
(c) 0.129 k
(d) 0. 120 kJ
Answer:
(b) 0.109 kJ
Solution:
∆Hvap = 2.257 kJ g-1
1 mole of H2O = 18 g
∴∆Hvap for 1 mole = 2.257 x 18 = 40.626 k J g-1
Tb = 373K
∆Hvap = \(\frac{40.626}{373}\) = 0.1089 KJ g-1
= 0.109 kJ mol-1
Question 29.
Which of the following units represent largest amount of energy?
(a) calories
(b) Joule
(c) erg
(d) eV
Answer:
(a) calories
Question 30.
The intensive property among these quantities is
(a) mass
(b) volume
(c) enthalpy
(d) mass / volume
Answer:
(d) mass /volume
Question 31.
System in which there is no exchange of matter, work or energy from surrounding is
(a) closed
(b) isolated
(c) adiabatic
(d) isothermal
Answer:
(b) isolated
Question 32.
Which of the following is not an intensive property?
(a) Pressure
(b) Density
(c) Volume
(d) Surface tension
Answer:
(c) Volume
Question 33.
A gas can expand from loo ml to 250 ml under constant pressure of 2 atm. The work done by the gas is ………..
(a) -30.39 J
(b) 25 J
(c) 5 kJ
(d) 16 J
Answer:
(a) -30.39 J
Solution:
∆V = expansion in volume = 100 to 250
∆V = V2 – V2 = 250 – 100
∆V = 150 ml = 0.15 litre
Work done = ?
Pressure = 2 atm
w = -P∆V
= -2 x 0.15 litre x 101.3 JL-1 atm-1
= -30.39 J.
![]()
Question 34.
An ideal gas expands in volume from 1 x 10-3 m3 to 1 x 10-2 m3 at 300K against a constant pressure at 1 x 105 Nm5. The work done is ………..
(a) -900 J
(b) 900 kJ
(c) 270 kJ
(d) -900 kJ
Answer:
(a) -900 J
Question 35.
Identify the state quantity among the following
(a) q
(b) q – w
(c) q + w
(d) q/w
Answer:
(b) q – w
Question 36.
In general, for an exothermic reaction to be spontaneous
(a) temperature should be high
(b) temperature should be zero
(c) temperature should be low
(d) temperature has no effect
Answer:
(c) temperature should be low
Question 37.
Heat of neutralization of a strong acid by a strong base is a constant value because
(a) only OH+ and OH– ions react in every case
(b) the strong base and strong acid react completely
(c) the strong base and strong acid react in aqueous solution
(d) salt formed does not hydrolyse
Answer:
(a) only OH+ and OH– ions react in every case
Question 38.
The heat absorbed at constant volume is equal to the system’s change in
(a) enthalpy
(b) entropy
(c) internal energy
(d) free energy
Answer:
Answer:
(c) internal energy
Question 39.
Heat of neutralization is always
(a) positive
(b) negative
(c) zero
(d) positive or negative
Answer:
(b) negative
![]()
Question 40.
The heat of formation CO and CO2 are -26.4 Kcal and -94 Kcal respectively. Heat of combustion of carbon monoxide will be …………
(a) + 26.4 KCal
(b) – 67.6 KCal
(c) – 120.6 K Cal
(d) + 52.8 K Cal
Answer:
(b) -67.6 KCal
Solution:
C + ½ O2 → CO ∆H = -26.4 K.cal ……….(1)
C + O2 → CO2 ∆H = -94 K.cal ……..(2)
Heat of combustion of CO is
C + ½O2 → CO2 ∆H = ?
Equation (1) is reversed.

ΔH= -67.6 K. cal
Question 41.
For the reaction H2 + I2 ⇌ 2HI, ∆H = 12.40 Kcal the heat of formation of HI is ……….
(a) 12.4 Kcal mol-1
(b) -12.4 Kcal mol-1
(c) -6.20 Kcal mol-1
(d) 6.20 Kcal mol-1
Answer:
(d) 6.20 Kcal mol-1
Solution:
H2 + I2 → 2HI ∆H = 12.40K.cal
½ H2 + ½ I2 → HI = ∆H/2
∴ \(\frac {12.40}{2}\) = 6.20 K.cal mol-1.
Question 42.
Heat capacity is ……….
(a) \(\frac {dq}{dT}\)
(b) dq.dT
(c) ∑q. \(\frac {1}{dT}\)
(d) none of these
Answer:
(a) \(\frac {dq}{dT}\)
Question 43.
The relation between Cp and Cv is…………
(a) Cp – Cv = R
(b) Cp + Cv = R
(c) – 285 KJ
(d) R – Cv = Cp
Answer:
(a) Cp – Cv = R
Question 44.
The heat required to raise the temperature of a body by I K is called ……….
(a) specific heat
(b) thermal capacity
(c) water equivalent
(d) none of these
Answer:
(b) thermal capacity
Question 45.
Heat liberated when 100 ml of IN NaOH is neutralized by 300 ml of in HCl ………..
(a) 22.92 Ici
(b) 17.19 kJ
(c) 11.46 kJ
(d) 5.73 Id
Answer:
Base = V1 = 100ml
N1 = 1N
Acid = V2 = 300ml
N2 = 1N
Enthalpy of neutralization of 1000 ml = 57.3 kJ.
∴ Enthalpy of neutralization of 100 ml x 100 = \(\frac {5.73 kJ}{1000}\) x 100 = 5.73 kJ.
![]()
Question 46.
In order to decompose 9g of water, 142.5 kJ of heat is required. Hence enthalpy of formation of water is ………..
(a) -142.5 kJ
(b) 142.5 kJ
(c) -285 kJ
(d) 285 kJ
Answer:
(c) -285 kJ
Solution:
H2O → H2 + ½ O2
18(g)
9g H2O is decomposed by – 142.5 kJ amount of heat.
:. 18g H2O will be decomposed by ![]() = +285 kJ.
= +285 kJ.
:. 18g of H2O is formed by – 285 kJ amount of heat. (Evolution of heat = – ve sign)
Question 47.
Assertion (A) : Combustion of all organic compounds is an exotherinic reaction ………….
Reason (R) : The enthalpies of all elements in their standard state are zero.
Which of the above statement isare not correct?
(a) both A and R are true and R is the correct explanation of A
(b) both A and R are true and R is not correct explanation of A
(c) both A and R are false
(d) A is false but R is true
Answer:
(b) both A and R are true and R is not correct explanation of A
Question 48.
Assertion (A) : Spontaneous process is an irreversible process and may be reversed by same external agency.
Reason (R) : Decrease in enthalpy is a contributory factor for spontaneity.
(a) both A and R are true and R is the correct explanation of A
(b) both A and R are true and R is not correct explanation of A
(c) both A and R are false
(d) A is false but R is true
Answer:
(b) both A and R are true and R is not correct explanation of A
Question 49.
Assertion (A) : A liquid crystallizes into a solid and accompanied by decrease in entropy.
Reason (R) : In crystals molecules are organised in an ordered manner.
(a) both A and R are true and R is the correct explanation of A
(b) both A and R are true and R is not correct explanation of A
(c) both A and R are false
(d) A is false but R is true
Answer:
(a) both A and R are true and R is the correct explanation of A
Question 50.
Thermodynamics is applicable to ………….
(a) macroscopic system only
(b) microscopic system only Thermodynamics
(c) homogeneous system only
(d) heterogeneous system only
Answer:
(a) macroscopic system only
Question 51
An isochoric process takes place at constant …………
(a) temperature
(b) pressure
(c) volume
(d) concentration
Answer:
(c) volume
![]()
Question 52.
For a cyclic process, the change in internal energy of the system is …………
(a) always + ve
(b) equal to zero
(c) always – ve
(d) none of the above
Answer:
(b) equal to zero
Question 53.
Which of the following properties is not a fùnction of state?
(a) Concentration
(b) Internal energy
(c) Enthalpy
(d) Entropy
Answer:
(u) Concentration
Question 54.
Which of the following relation is true?
(a) Cp >Cv
(b)Cv > Cp
(c) Cp = Cv
(d) Cp = Cv = 0
Answer:
(a) Cp >Cv
Question 55.
Which of the following always has a negative value?
(a) heat of reaction
(b) heat of solution
(c) heat of combustion
(d) heat of formation
Answer:
(c) beat of combustion
Question 56.
The bond energy depends upon ………..
(a) size of the atom
(b) electronegativity
(c) bond length
(d) all of the above
Answer:
(d) all of the above
Question 57.
For an endothermic reaction ………..
(a) ∆H is -ve
(b) ∆H is +ve
(e) ∆H is zero
(d) none of these
Answer:
(b) AH is +ve
Question 58.
The process depicted by the equation.
H2O(s) → H2O(l)
∆H = + 1.43 kcal represents
(a) fusion
(b) melting
(c) evaporation
(d) boiling
Answer:
(a) fusion
Question 59
Which one is the correct unit for entropy?
(a) KJ mol
(b) JK-1 mol
(c) JK-1 mol-1
(d) KJ mol-1
Answer:
(c) JK-1 mol-1
Question 60.
A thermodynamic state function is a quantity ………….
(a) used to determine heat changes
(b) whose value is independent of path
(c) used to determine pressure volume work
(d) whose value depends on temperature only
Answer:
(b) whose value is independent of path
![]()
Question 61.
For the process to occur under adiabatic conditions, the correct condition is ………..
(a) ∆T = 0
(b) ∆p = 0
(c) q = 0
(d) w = 0
Answer:
(c) q = 0
Question 62.
The enthalpies of all elements in their standard states are …………
(a) unity
(b) zero
(c) <0
(d) different for each element
Answer:
(b) zero
Question 63.
∆\({ U }^{ \ominus }\) of combustion of methane is -X kJ mol-1. The value of ∆He is ………..
(a) = ∆\({ U }^{ \ominus }\)
(b) > ∆\({ U }^{ \ominus }\)
(c) < ∆\({ U }^{ \ominus }\)
(d) 0
Answer:
(c) < ∆U\({ U }^{ \ominus }\)
Question 64.
The enthalpy of combustion of methane, graphite and dihydrogen at 298K are -890.3 kJ mol-1 -393.5 kJ mol-1 and 285.8 kJ mol-1 respectively. Enthalpy of formation of CH4 will be ………..
(a) – 74.8 kJ mol-1
(b) – 52.27 k mol-1
(c) 74.8 kJ mol-1
(d) + 52.26 kJ mol-1
Answer:
(a) – 74.8 kJ mol-1
Solution:
CH4 + 3O4 → CO + 2H2O ∆H1 = – 89O.3 kJ mol-1 ……….(1)
C + O2 → CO2 = -393.5 kJ mol-1 ……….(2)
H5 + 1/2 O2 → H2O = – 285.8 kJ mol-1 ……….(3)
Equation (1) is reversed.
Equation (3) x 2

∆Hf = +890.3 – 965.1 = -74.8 KJ mol-1
Question 65.
A reaction, A + B → C + D + q is found to have a positive entropy change. The reaction will be ………..
(a) possible at high temperature
(b) possible only at low temperature
(c) not possible at any temperature
(d) possible at any temperature
Answer:
(d) possible at any temperature
Question 66.
Consider the following statements.
(i) Thermodynamics is independent of atomic and molecular structure.
(ii) It includes whether a particular reaction is feasible or not under a given set of temperature and concentration of reactants and products.
(iii) It can determine the rate at which the reaction take place.
Which of the above statements is/are not correct’?
(a) (i) only
(b) (ii) only
(c) (iii) only
(d) (i) and (ii) only
Answer:
(c) (iii) only
![]()
Question 67.
A fundamental goal of thermodynamics is the …………
(a) prediction of spontaneity of the reaction.
(b) determination of rate of the chemical reaction.
(c) evaluation of the microscopic properties.
(d) both (b) and (c)
Answer:
(a) prediction of spontaneity of the reaction.
Question 68.
The first law of thermodynamics states that …………
(a) ∆U = q – w
(b) ∆U = q + w
(c) ∆U + q = w
(d) ∆U = w – q
Answer:
(b) ∆U = q + w
Question 69.
Anything which separates the system from its surroundings is called …………..
(a) Boundary
(b) Partition
(c) Universe
(d) Outer layer
Answer:
(a) Boundary
Question 70.
Hot water in a thermos flask is an example of ………….
(a) closed system
(b) open system
(c) isolated system
(d) isochoric system
Answer:
(c) isolated system
![]()
Question 71.
Which one of the following is an example for closed system?
(a) Hot water contained in a thermos flask
(b) A gas contained in a cylinder fitted with a piston
(c) All living things
(d) Hot water contained in a open beaker
Answer:
(b) A gas contained in a cylinder fitted with a piston
Question 72.
Statement-I: All living things are open systems.
Statement-II: Because they continuously exchange matter and energy with the surroundings
(a) Statement-I and II arc correct and Statement-II is the correct explanation of Statement-I
(b) Statement-I and II are correct but Statement-II is not the correct explanation of Statement-I
(c) Statement-I is correct and Statement-II is wrong.
(d) Statement-I is wrong but Statement-II is correct.
Answer:
(a) Statement-I and II are correct and Statement-II is the correct explanation of Statement-I.
Question 73.
Which one of the following is an extensive property?
(a) Molar volume
(b) Density
(c) Molaritv
(d) Entropy
Answer:
(d) Entropy
Question 74.
Which one of the following is ail intensive property?
(a) Specific heat capacity
(b) Mass
(c) Enthalpy
(d) Heat capacity
Answer:
(a) Specific heat capacity
Question 75.
Which one of the following is not an extensive property?
(a) Mole
(b) Energy
(c) Molar mass
(d) Free energy
Answer:
(c) Molar mass
Question 76.
Which one of the following is not an intensive property?
(a) Density
(b) Molaritv
(c) Molality
(d) Mole
Answer:
(d) Mole
![]()
Question 77.
Which one of the following depend on the mass of the system?
(a) Density
(b) Mole fraction
(c) Mass
(d) Molar mass
Answer:
(c) Mass
Question 78.
Which one of the following is independent to the mass of the system?
(a) Volume
(b) Enthalpy
(c) Entropy
(d) Density
Answer:
(d) Densily
Question 79.
The process in which there is no exchange of heat between thc system and surrounding is called ……….
(a) Adiabatic process
(b) Isothermal process
(c) Isobaric process
(d) Isochoric process
Answer:
(a) Adiabatic process.
Question 80.
For an adiabatic process …………..
(a) dU = 0
(b) dT = 0
(c) q = 0
(d) q = w
Answer:
(c) q = 0
Question 81.
For an isothermal process …………..
(a) dH = 0
(b) dP = 0
(c) dT = 0
(d) dV = 0
Answer:
(c) dT = 0
Question 82.
The process in which the volume of the system remains constant is called ……….
(a) Adiabatic process
(b) Isothermal process
(c) Isobaric process
(d) Isochoric process
Answer:
(d) Isochoric process
![]()
Question 83.
For an isochoric process ……………
(a) q = 0
(b) dp = O
(c) dv = O
(d) ∆U = 0
Answer:
(c) dv = O
Question 84.
Combustion of fuel in a bomb calorimeter is an example of …………
(a) adiabatic process
(b) isochoric process
(c) isobaric process
(d) isothemal process
Answer:
(b) isochoric process
Question 85.
Which one of the following is not a path function?
(a) Work
(b) Heat
(c) Pressure
(d) Either (a) or (b)
Answer:
(c) Pressure
Question 86.
Which one of the following is a path function?
(a) Pressure
(b) Volume
(c) Temperature
(d) Heat
Answer:
(d) Heat
Question 87.
Which one of the following is a state function?
(a) Internal energy
(b) Enthalpy
(c) Free energy
(d) All the above
Answer:
(d) All the above
Question 88.
Statement-I: Internal energy of a system is an extensive property.
Statement-II: Internal energy depends on the amount of the substances present in the system.
(a) Statement-I and II are correct and Statement-II is the correct explanation of Statement-I.
(b) Statement-I and II arc correct hut Statement-II is not the correct explanation of Statement-I.
(c) Statement-I is correct but Statement-II is wrong.
(d) Statement-I is wrong but Statement-II is correct.
Answer:
(a) Statement-I and II are correct and Statement-II is the correct explanation of Statement-I.
Question 89.
The SI unit of heat is ………..
(a) Joule
(b) Kelvin
(c) Kg
(d) Kg mol-1
Answer:
(a) Joule
Question 90.
Which one of the following is the quantity of heat required to raise the temperature of I gm of water by 1 °C?
(a) 1 Joule
(b) 1 Calorie
(c) 1 Kelvin
(d) 1 Kilo joule
Answer:
(b) 1 Calorie
![]()
Question 91.
Which one of the following is equal to 1 Joule?
(a) Nm-1
(b) Nm2
(c) Nm
(d) Kg ms-2
Answer:
(c) Nm
Question 92.
Consider the following statements.
(i) Work is a state function.
(ii) Work brings a temporary effect in the surroundings.
(iii) Work appears only at the boundary of the system.
Which of the above statements is/are not correct?
(a) (iii) only
(b) (i) and (ii)
(c) (i) and (iii)
(d) (ii) and (iii)
Answer:
(b) (i) and (ii)
Question 93.
Which of the following represents the gravitational work ?
(a) QV
(b) F. x
(c) mgh
(d) -P∆V
Answer:
(c) mgh
Question 94.
Match the List-I and List-II using the correct code given below the list.

Answer:
![]()
Question 95.
Match the List-I and List-II using the correct code given below the list.
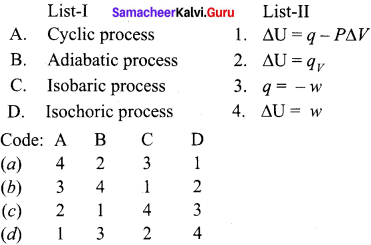
Answer:
![]()
Question 96.
Enthalpy is defined as ………..
(a) q + w
(b) q – P∆V
(c) U + PV
(d) w
Answer:
(c) U + PV
Question 97.
Which one of the following always he negative?
(a) Enthalpy of combustion
(b) Enthalpy of fusion
(c) Enthalpy of vapourisation
(d) Enthalpy of sublimation
Answer:
(a) Enthalpy of combustion
![]()
Question 98.
For an ideal gas …………
(a) Cp – CV = O
(b) Cp – CV = R
(c) CV – Cp = R
(d) CV – Cp > R
Answer:
(b) Cp – CV = R
Question 99.
The standard substance used in the enthalpy of combustion of a substance in bomb calorimeter is …………
(a) methane
(b) acetic acid
(c) propane
(d) benzoic acid
Answer:
(d) benzoic acid
Question 100.
The standard value of enthalpy of combustion of benzoic acid is …………
(a) – 3227 kJ mol-1
(b) + 3227 kJ mol-1
(c) – 32.27 Ici mol-1
(d) + 32.27 kJ mol-1
Answer:
(a) -3227 kJ mol-1
Question 101.
The heat of neutralization of a strong acid and strong base is around …………
(a) + 57.32 kJ
(b) – 57.32 kJ
(c) – 3227 kJ mol-1
(d) + 3227 kJ mol-1
Answer:
(b) – 57.32 kJ
Question 102.
Which of the following is not a spontaneous process?
(a) All water fall runs down hill.
(b) A lump of sugar dissolves in cup of coffee.
(c) Heat flow from hotter object to colder one.
(d) A water flow from a well to upper reservoir.
Answer:
(d) A water flow from a well to upper reservoir.
Question 103.
Which one of the following is an endothermic process?
(a) CH4 + 2O2 → CO2 + 2H2O
(b) H+ + OH– → H2O
![]()
(d) C + O2 → CO2
Answer:
![]()
Question 104.
The SI unit of entropy is …………
(a) Nm
(b) Cal mol-1
(c) KJ mol-1
(d) JK-1
Answer:
(d) JK-1
Question 105.
In which of the following entropy decreases?
(a) melting of ice
(b) evaporation of water
(c) crystallization of sugar
(d) dissolution of salt
Answer:
(c) crystallization of sugar
![]()
Question 106.
Gibbs’s free energy is defined as ………….
(a) G = H+ TS
(b) G = H x TS
(c) G = H – TS
(d) G = H/TS
Answer:
(c) G = H – TS
Question 107.
Match the List-I and List-II using the correct code given below the list.

Answer:
![]()
Question 108.
Van’t Hoff equation is ………….
(u) ∆G° = AH° – T∆S°
(b) G = H – TS
(c) ∆G° = -2.303 RT log Keq
(d) ∆S = ∆H / T
Answer:
(c) ∆G° = -2.303 RT log Keq
Question 109.
Mathematically, the third law of thermodynamics is expressed as ………..
(a) ![]()
(b) ![]()
(c) AU = q + w
(d) G = H – TS
Answer:
(a) ![]()
II. Answer briefly (2 or 3 marks)
Question 1.
Define isolated system.
Answer:
A system which can exchange neither matter nor energy with its surroundings is called an isolated system. Here boundary is sealed and insulated.
Question 2.
What is the scope of thermodynamics?
Answer:
The scope of thermodynamics:
- To derive feasibility of a given process.
- It also helps in predicting how far a physical (or) chemical change can proceed. until the equilibrium conditions are established.
Question 3.
Illustrate the Closed system with an example.
Answer:
Hot water contained in a closed beaker is an example for a closed system. In this system energy (heat) is transferred to the surroundings but no matter (water vapour) can escape from this system. A gas contained in a cylinder fitted with a piston constitutes a closed system.
Question 4.
Define
1. System
2. Surroundings.
Answer:
1. System:
A system is defined as any portion of matter under thermodynamic consideration. which is separated from the rest of the universe by real or imaginary boundaries. e.g.. Water taken in a beaker, balloon filled with air, seed, plant, flower and bird.
2. Surroundings:
Everything in the universe that is not the part of system and can interact with system is called as surroundings.
![]()
Question 5.
What is meant by isolated system? Give example.
Answer:
- A system which can exchange neither matter nor energy with its surroundings is called an isolated system.
- Here boundary is scaled and insulated.
- Hot water contained in a thermos flask, is an example for an isolated system.
Question 6.
Explain a closed system with an example.
Answer:
- A system which can exchange only energy but not matter with its surroundings is called a closed system.
- Here the boundary is sealed but not insulated.
- Hot water contained in a closed beaker is an example for a closed system.
- In this system heat is transferred to the surroundings but no water vapour can escape from this system.
- A gas contained in a cylinder fitted with a piston constitutes a closed system.
Question 7.
Define enthalpy.
Answer:
The enthalpy (H), which is a thermodynamic property of a system, is defined as the sum of the internal energy (U) of a system and the product of pressure and volume of the system.
H = U + PV
Question 8.
What are extensive properties?
Answer:
- The property that is depend on the mass or size of the system is called an extensive property.
- e.g., Volume, number of moles, mass and internal energy.
Question 9.
What is reversible process? Give an example.
Answer:
The process in which the system and surroundings can be restored to the initial state from the final state without producing any changes in the thermodynamics properties of the Universe is called a reversible process. e.g.,
H2 + I2 ⇌ 2HI
Question 10.
What is an irreversible process? Give an example.
Answer:
- The process in which the system and surroundings cannot be restored to the initial state from the final state is called a reversible process.
- e.g.. All the processes occurring in nature are irreversible processes.
Question 11.
Define cyclic process. Give example.
Answer:
When a system returns to its original state after completing a series of changes, then it is said that a cycle is completed. This process is known as a cyclic process. For a cyclic process dU = 0, dH= 0, dP = 0, dV= 0 and dT= 0.
Question 12.
What is meant by internal energy?
Answer:
- Internal energy (U) of a system is equal to the energy possessed by all its constituents namely atoms, ions and molecules.
- The energy of a molecule is equal to the sum of its translational energy (Uv), vibrational energy (Ub), rotational energy (Ue), bond energy (jh’ electronic energy and energy due to molecular interactions (Ui).
- U = Ut + Uv + Ur + Ub + Ue + Ui
- The total energy of all the molecules of the system is called internal energy.
Question 13.
Define Heat. Give its unit.
Answer:
- Heat (q) is regarded as energy in transit across the boundary separating a system from its
surroundings. - Heat changes result in temperature differences between system and surroundings.
- Heat is a path function.
- Units of heat: SI unit of heat is the joule (J).
Question 14.
Write a note about the sign convention of heat.
Answer:
- The symbol of heat is q.
- if the heat flows into the system from the surroundings, the energy of a system increases. Hence it is taken to be positive (+ q).
- if heat flows out of the system into the surroundings. energy of the system decreases. Hence it is taken to be negative (- q).
Question 15.
What is meant by work? Give its unit.
Answer:
- Work is defined as the force (F) multiplied by the displacement (x).
- – w = F. x
- Minus (-) sign indicates the work done by the system
- Unit of work: The SI unit of work is Joule (J).
Question 16.
Explain about gravitational work. Give its unit.
Answer:
1. When an object is raised to a certain height against the gravitational field, gravitational work is done on the object.
2. For example, if an object of mass ‘m’ is raised through a height ‘h’ against acceleration due to gravity ‘g’, then the gravitational work carried out is ‘mgh’.
w = m.g.h
w = Kg .ms-2.m
w = Kg m2 s-2
w = Joule
![]()
Question 17.
Define electrical work. Give its unit.
Answer:
- When a charged body moves from one potential region to another electrical work is done.
- If the electrical work done is QV. Where V is the potential difference and Q is the quantity of electricity.
w = QV
w = Coulomb . Volts
w = Joule
Question 18.
Write a note about mechanical work. Give its unit.
Answer:
- Mechanical work is defined as force multiplied by the displacement through which the force acts.
- Whenever a force (F) acts on an object and the object undergoes a displacement (x) in the direction of the force, then the mechanical work is said to be done.
- Mathematically w = F . x
w = F. x = N.m
w = Joule
Question 19.
Define Zeroth law of thermodynamics (or) Law of thermal equilibrium.
Answer:
Zeroth law of thermodynamics states that ‘If two systems at different temperatures are separately in thermal equilibrium with a third one, then they tend to be in thermal equilibrium with themselves’.
Question 20.
Define enthalpy of a system. Give its unit.
Answer:
Enthalpy is a thermodynamic property of a system. Enthalpy (H) is defined as sum of the internal energy (U) of a system and the product of pressure and volume of the system.
H = U + PV
Unit of enthalpy: KJ mol-1.
Question 21.
Define standard heat of formation.
Answer:
The standard heat of formation of a compound is defined as “The change in enthalpy that takes place when one mole of a compound is formed from its elements, all substances being in their standard states (298 K and 1 atm pressure).
Question 22.
Define specific heat capacity of a system.
Answer:
Specific heat capacity of a system is defined as the heat absorbed by one gram of a substance in raising its temperature by one Kelvin at a specified temperature.
Cm = \(\frac{q}{\left(\mathrm{T}_{2}-\mathrm{T}_{1}\right)}\)
Where C specific heat capacity, q = amount otheat absorbed. m = mass and T1,T2 temperatures.
![]()
Question 23.
Derive the value of molar heat capacity as constant volume.
Answer:
According to the first law of themrndynamics,
dq = dU + PdV
Dividing both sides by dT, we have
\(\frac {dq}{dT}\) = \(\frac {(dU + PdV)}{dT}\)
At constant volume dV = 0,then
\(\frac {dq}{dT}\) = (\(\frac {dU}{dT}\))V
CV = (\(\frac {dU}{dT}\))V
Thus the heat capacity ai constant volume (CV ) is defined as the rate of change of internal energy with respect to temperature at constant volume.
Question 24.
Derive the value of molar heat capacity at constant pressure.
Answer:
We know.
H = U + PV
Differentiating the above equation with respect to temperature at constant pressure we get,
(\(\frac {dH}{dT}\))P = ?(\(\frac {dU}{dT}\))P + P(\(\frac {dV}{dT}\))P
We know,
C = \(\frac {dq}{dT}\)
But at constant pressure dq = dH
Hence we get,
CP = (\(\frac {dH}{dT}\))P
Thus heat capacity at constant pressure (CP) is defined as the rate of change of enthalpy with respect to temperature at constant pressure.
Question 25.
Prove that for an ideal gas, CP is greater than CV.
Answer:
1. It is clear that two heat capacities are not equal and CP is greater than CV by a factor which is related to the work done.
2. At a constant pressure, a part of heat absorbed by the system is used up in increasing the internal energy of the system and the other for doing work by the system.
3. At constant volume, the whole of heat absorbed is utilized in increasing the temperature of the system as there is no work done by the system. Thus CP is greater than CV.
CP = \(\frac {dH}{dT}\) ; CV = \(\frac {dU}{dT}\)
4. By definition, H = U + PV for 1 mole of an ideal gas.
H = U + RT
By differentiating this equation with respect to temperature T. we get,
\(\frac {dH}{dT}\) = \(\frac {dU}{dT}\) + R
CP = CV + R
CP – CV = R
Thus for an ideal gas, CP is greater than CV by the gas constant R.
![]()
Question 26.
What are the applications of Bomb Calorimeter?
Answer:
- Bomb calorimeter is used to determine the amount of heat released in combustion reaction.
- It is used to determine the calorific value of food.
- Bomb calorimeter is used in many industries such as metabolic study. food processing and
explosive testing.
Question 27.
Define heat of solution.
Answer:
The heat of solution is defined as “the change in enthalpy of the system when one mole of a substance is dissolved in a specified quantity of solvent at a given temperature”.
Question 28.
Define molar heat of fusion.
Answer:
The molar heat of fusion is defined as “the change in enthalpy when one mole of a solid substance is converted into the liquid state at its melting points’.
Question 29.
What is meant by molar heat of vapourisation?
Answer:
The molar heat of vapourisation is defined as the change in enthalpy when one mole of liquid is converted into vapour or gaseous state at its boiling point.
Question 30.
- What is sublimation?
- Define molar heat of sublimation.
Answer:
- Sublimation is a process when a solid changes directly into gaseous state without changing into liquid state.
- Molar heat of sublimation is defined as the change in enthalpy when one mole of a solid is directly converted into the gaseous state at its sublimation temperature.
Question 31.
Define heat of transition?
Answer:
The heat of transition is defined as the change in enthalpy when one mole of an element changes from one allotropic form to another.
Question 32.
How do you measure the enthalpy of formation of carbon monoxide?
Answer:
1. Hess’s law can be applied to calculate the enthalpy of formation of carbon monoxide. It is very difficult to control the oxidation of graphite to give pure CO. However, enthalpy for the oxidation of graphite to CO2 can be easily measured and enthalpy of oxidation of CO to CO2 is also measurable.
2. The application of Hess’s law enables us to estimate the enthalpy of formation of CO.
C + O2 → CO2 ∆H° = 393.5 kJ ……….. (1)
CO + 1/2 O2 → CO2 ∆H° = -283 kJ ……….. (2)
on inverting equation (2), we get
CO2 → CO + 1/2 O2 ∆H° = + 283 kJ ………… (3)
on adding equations (2) and (3), we get
C + 1/2 O2 → CO ∆H°= 393 5 + 283 = 110.5kJ
![]()
Question 33.
What are the important features of lattice enthalpy?
Answer:
1. Higher lattice energy shows greater electrostatic attraction and therefore a stronger bond in the solid.
2. The lattice enthalpy is greater for ions of higher charge and smaller radii.
Question 34.
Why there is a need for second law of thermodynamics? Give its importance.
Answer:
- Thermodynamics first law tells that there is an exact equivalence between various forms of energy and that heat gained is equal to heat loss.
- Practically it is not possible to convert the heat energy into an equivalent amount of work.
- To explain this, another law is needed which is known as second law of thermodynamics.
- The second law of thermodynamics helps us to predict whether the reaction is feasible or not and also tell the direction of the flow of heat.
- It also tells that energy cannot be completely converted into equivalent work.
Question 35.
Write the entropy statement of second law of thermodynamics.
Answer:
Whenever a spontaneous process takes place, it is accompanied by an increase in the total entropy of the Universe.
∆Suniverse > ∆Ssystem + ∆Ssurroundings
Question 36.
Write the Clausius statement of second law of thermodynamics.
Answer:
Clausius statement: Heat flows spontaneously from hot objects to cold objects and to get it flow in the opposite direction, we have to spend some work.
Question 37.
What are spontaneous reaction? Give three examples for spontaneous reaction.
Answer:
reaction that does occur under the given set of conditions is called a spontaneous reaction.
Example:
- A waterfall runs downhill, but never up, spontaneously.
- Heat flows from hotter object to a colder one.
- Ageing process.
Question 38.
Define standard entropy of formation.
Answer:
Standard entropy of formation is defined as “the entropy of formation of 1 mole of a compound from the elements under standard conditions”. It is denoted as ∆Sf°. We can calculate the value of entropy of a given compound from the values of S° of elements.
∆Sf° = ∑∆Sproducts° – ∑∆Sreactants°
Question 39.
What is entropy of fusion?
Answer:
When one mole of the solid melts at its melting point reversibly the heat absorbed is called molar heat of fusion. The entropy change is given by
∆Sf = \(\frac{\Delta \mathrm{H}_{f}}{\mathrm{T}_{f}}\)
Where ∆Hf = molar heat of fusion, Tf is melting point.
![]()
Question 40.
What is entropy of Vapourisation?
Answer:
When one mole of liquid is boiled at its boiling point reversibly, the heat absorbed is called as molar heat of vaporization. The entropy change is given by
∆Sv = \(\frac{\Delta \mathrm{H}_{v}}{\mathrm{T}_{b}}\)
where ∆Hv is molar heat of vapourisation. Tb is boiling point.
Question 41.
Define entropy of transition.
Answer:
When one mole of a solid changes reversibly from one allotropic form to another at its transition temperature. The entropy change is given
∆St = \(\frac{\Delta \mathrm{H}_{t}}{\mathrm{T}_{t}}\)
Where ∆Ht = molar heat of transition and Tt = transition temperature.
Question 42.
Explain the following:
- Out of diamond and graphite, which has greater entropy? Why?
- From thermodynamic point of view, in which system the animals and plants belong?
Answer:
- Graphite has greater entropy, because it is loosely packed.
- Animals and plants belong to open system.
Question 43.
What is the condition spontaneity in terms of free energy change?
Answer:
- If ∆G is negative, process is spontaneous.
- if ∆G is positive, process is non-spontaneous.
- if ∆G = 0, the process is in equilibrium.
Question 44.
Why standard entropy of an elementary substance is not zero whereas standard enthalpy of formation is taken as zero?
Answer:
A substance has a perfectly ordered arrangement only at absolute zero. Hence, entropy is zero only at absolute zero. Enthalpy of formation is the heat change involved in the formation of one mole of the substance from its elements. An element formed from its constituents means no heat change.
![]()
Question 45.
The equilibrium constant for a reaction is one or more if ∆G ° for it is less than zero. Explain.
Answer:
\({ G }^{ \ominus }\) = – RT in K, thus if \({ G }^{ \ominus }\) is less than zero Le., it is negative, then In K will be positive and hence K will be greater than one.
Question 46.
Many thermo dynamically feasible reactions do not occur under ordinary conditions. Why?
Answer:
Under ordinary conditions, the average energy of the reactants may be less than threshold energy. They require some activation energy to initiate the reaction.
Question 47.
Predict in which of the following, entropy increases or decreases.
Answer:
- A liquid crystallizes into a solid
- Temperature of a crystallized solid is raised from 0 K to 115 K
- 2NaHCO3(s) → NaCO2CO3(s) + CO2(s) + H2O(s)
- H2(s) → 2H(g)
Answer:
- After freezing, the molecules attain an ordered state and therefore, entropy decreases.
- At O K the constituent particles are in static form therefore, entropy is minimum. If the temperature is raised to 115 K particles begin to move and entropy increases.
- Reactant, NaHCO3 is solid. Thus, its entropy is less in comparison to product which has high entropy.
- Here, one molecule gives two atoms. Thus, number of particles increases and this leads to more disordered form.
Samacheer Kalvi 11th Chemistry Thermodynamics 5 – Mark Questions
Question 1.
Explain how heat absorbed at constant pressure is measured using coffee cup calorimeter with neat diagrani.
Answer:
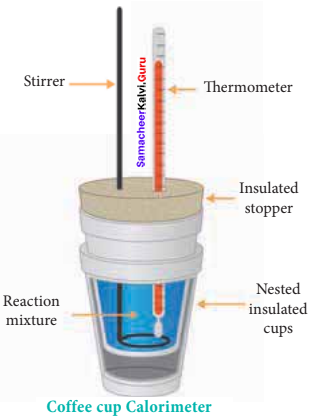
- Measurement of heat change at constant pressure can be done in a coffee cup calorimeter.
- We know that ∆H = qp (at constant P) and therefore, heat absorbed or evolved, qp at constant pressure is also called the heat of reaction or enthalpy of reaction, ∆Hr
- in an exoihermic reaction, heat is evolved, and system loses heat to the surroundings. Therefore, qp will be negative and ∆Hr will also be negative.
- Similarly in an endothermic reaction, heat is absorbed, qp is positive and ∆Hr will also be positive.
Question 2.
List the characteristics of entropy.
Characteristics of entropy:
Answer:
- Entropy is a thermodynamic state function that is a measure of the randomness or disorderliness of the system.
- In general, the entropy of gaseous system is greater than liquids and greater than solids. The symbol of entropy is S.
- Entropy is defined as for a reversible change taking place at a constant temperature (T), the change in entropy (∆S) of the system is equal to heat energy absorbed or evolved (q) by the system divided by the constant temperature (T).
\(\Delta S_{\text {sys }}=\frac{q_{\text {rev }}}{T}\) - If heat is absorbed, then AS is positive and there will be increase in entropy. If heat is evolved, ∆S is negative and there is a decrease in entropy.
- The change in entropy of a process represented by AS and is given by the equation,
∆Hsys = Sf – Si - If Sf> Si, ∆S is positive, the reaction is spontaneous and reversible. If Sf < Si, ∆S is negative, the reaction is non-spontaneous and irreversible.
- Unit of entropy: SI unit of entropy is J K ‘.
Question 3.
Explain about the characteristics of work.
Characteristics of work:
Answer:
- Work is defined as the force (F) multiplied by the displacemcnt (x).
– w = F.x ……… (1)
The – ve sign is introduced to indicate that the work has been done by the system by spending a part of its internal energy. - Work is a path function.
- Work appears only at the boundary of the system.
- Work appears during the change ¡n the state of the system.
- Work brings a permanent effect in the surroundings.
- Units of work: The SI unit of work is the joule (J) or Kilojoule (KJ).
- If work done by the system, the energy of the system decreases, hence by convention work is taken to be negative (- w).
- If work done by the system, the energy of the system increases, hence by convention work is taken to be positive (+ w).
Question 4.
Derive the relationship between work for a reversible reaction and the charge in volume during comoression and expansion.
Answer:
1. During expansion, work is done by the system; since V1 > V1, the sign obtained for work will be negative.
2. During compression, work is done on the system; since V< V., the sign obtained for work will be positive.
3. If the pressure is not constant, but changes during the process such that it is always infinitesimally greater than the pressure of the gas, then, at each stage of compression, the volume decreases by an infinitesimal amount, dV.
4. We can calculate the work done on the gas by the relation,
w = –\(\int_{V_{i}}^{V_{f}} P d V\) …………(1)
5. In a compression process, Pext the external pressure is always greater than the pressure of the system. i.e., Pext = (Pint + dp). In an expansion process, the external pressure is always less than the pressure of the system i.e., Pext = (Pint – dp).
6. In general case, we can write, Pext = (Pint ± dp). Such processes are called reversible processes. For a compression process, work can be related to internal pressure of the system under reversible conditions by writing equation.
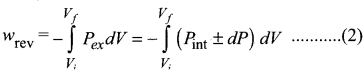
Since dp . dv is very small, we can write,
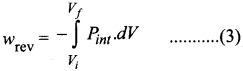
For a given system,
Pint V = nRT
Pint V = \(\frac {nRT}{V}\)

7. If Vf > Vi (expansion), the sign to work done by the process is negative.
If Vf < Vi (compression), the sign to work done by the process is positive.
![]()
Question 5.
Write the various definition of first law of thermodynamics.
First law of thermodynamics:
Answer:
- The total energy of an isolated system remains constant though it may change from one form to another.
- Whenever energy of a particular type disappears equivalent amount of another type must be produced.
- Total energy of a system and surroundings remains constant.
- Energy can neither be created nor destroyed, but may be converted from one form to another.
- The change in the internal energy of a closed system is equal to the energy that passes through its boundary as heat or work.
- Heat and work are equivalent ways of changing a systems internal energy.
Question 6.
Derive the various mathematical statements of the first law.
Answer:
Mathematical statement of the First law of Thermodynamics is
∆U = q + w
Case 1:
For a cyclic process involving isothermal expansion of an ideal gas
∆U = 0
∴ q = -w
In other words, during a cyclic process, the amount of heat absorbed by the system is equal to work done by the system.
Case 2:
For an isochoric process (no change in volume) there is no work of expansion.
∆V = 0
w = 0
∆U = 0
In other words, during isochoric process, the amount of heat supplied to the system is converted to its internal energy.
Case 3:
For an adiabatic process there is no change in heat .i.e., q O. Hence
q = 0
∆U = w
In other words, in an adiabatic process, the decrease in internal energy is exactly equal to the work done by the system on its surroundings.
Case 4:
For an isobaric process. There is no change in the pressure. P remains constant. Hence
∆U = q + w
∆U = q – P∆V
In other words, in an isobaric process a part of heat absorbed by the system is used for PV expansion work and the remaining is added to the internal energy of the system.
![]()
Question 7.
What are the characteristics of enthalpy?
Characteristics of enthalpy:
Answer:
1. Enthalpy is a thermodynamic property of a system. Enthalpy H is defined as sum of the internal energy (U) of a system and the product of pressure and volume of the system. That is,
H = U + PV
2. Enthalpy is a state function which depends entirely on the state functions T, P and U.
3. Enthalpy is usually expressed as the change in enthalpy (∆H) for a process between initial and final states.
∆H = ∆U + P∆V
4. At constant pressure, the heat flow (q) for the process is equal to the change in enthalpy which is defined by the equation.
∆H = qp
5. In an endothermic reaction heat is absorbed by the system from the surroundings that is q >0 (positive). Therefore, at constant Tand P, by the equation above, if q is positive then ∆H is also positive.
6. In an exothermic reaction heat is evolved by the system to the surroundings that is, q<0 (negative). If q is negative, then ∆H will also be negative.
7. Unit of enthalpy is KJ mol-1.
Question 8.
What are thermochemical equation? What are the conventions adopted In writing thermochemical equation?
Answer:
A thermochemical equation is a balanced stoichiometric chemical equation that includes the enthalpy change (∆H). Conventions adopted ¡n thermochemical equations:
- The coefficients in a balanced thermochemical equation refer to number of moles of reactants and products involved in the reaction.
- The enthalpy change of the reaction ∆H has unit kJ.
- When the chemical reaction is reversed, the value of AR is reversed in sign with the same magnitude.
- Physical states (gas, liquid, aqueous and solid) of all species is important and must be specified in a thermochemical reaction since AH depends on the phases of reactants and products.
- if the thermochemical equation is multiplied throughout by a number, the enthalpy change is also be multiplied by the same number value.
- The negative sign of ∆H indicates the reaction to be an exothermic and the positive sign of ∆H indicates an endothermic type of reaction.
Question 9.
Calculate the values of ∆U and ∆H for an ideal gas in terms of CP and CV
Calculation of ∆U and ∆H:
Answer:
For one mole of an ideal gas, we have
CV = \(\frac {dU}{dT}\)
dU = CV .dT
For a finite change, we have,
∆U = (U2 – U1) = CV (T2 – T1)
and for n moles of an ideal gas we get
∆U = nCV (T2 – T1) ………….(1)
We know,
∆H = ∆(U + PV)
∆H = ∆U + ∆(PV)
∆H = ∆U + ∆RT [: PV= RT]
∆H = ∆U + R∆T
∆H = CV (T2 – T1) + R (T2 – T1)
∆H = (CV + R) (T2 – T1)
∆H = CP (T2 – T1) [∴CP – CV = R]
For n moles of an ideal gas we get
∆H = n CP (T2 – T1) …………..(2)
![]()
Question 10.
Suggest and explain indirect method to calculate lattice enthalpy of magnesium bromide.
Answer:
Born Haber’s cycle method:
Mg(s) + Br2 (l) → MgBr2 ∆Hf°
Sublimation: Mg(s) → Mg(g) ∆H1°
Ionisation: Mg(g) → Mg2+(g) + 2e ∆H2°
Vapourisation: Br2(l) → Br2(g) ∆H3°
Dissociation: Br2(g) → 2Br(g)∆H4°∆H4°
Electron affinity: 2Br(g) + 2e– → 2Br–(g)∆H5°
Lattice enthalpy: Mg2+(g) + 2Br–(g) → MgBr2(s) ∆H6° = ?
∆Hf° = ∆H1° + ∆H1° + ∆H2° + ∆H3° + ∆H4° + ∆H5° + ∆H6°
∆H6° = ∆Hf° – (∆H1° + ∆H1° + ∆H2° + ∆H3° + ∆H4° + ∆H5°)
If we know the values of ∆Hf° , ∆H1°, ∆H2° , ∆H3° , ∆H4° and ∆H5°, we can calculate the value of ∆H6° by indirect method.
Question 11.
Derive the relationship between standard free energy (∆G°) and equilibrium constant (Keq).
Answer:
1. In a reversible process, system is at all times in perfect equilibrium with its surroundings.
2. A reversible chemical reaction can proceed in either direction simultaneously, so that a dynamic equilibrium is set up.
3. This means that the reactions in both the directions should proceed with decrease in free energy, which is impossible.
4. It is possible only ¡fat equilibrium, the free energy of a system is minimum.
5. Lets consider a general equilibrium reaction,
A + B ⇌ C + D
The free energy change of the above reaction in any state (∆G) is related to the standard free energy change of the reaction (∆G°) according to the following equation.
∆G = ∆G° + RT in Q …………(1)
where Q is reaction quotient and is defined as the ratio of concentration of the products to the concentration of the reactants under non-equilibrium condition.
6. When equilibrium is attained, there is no further free energy change i.e. ∆G = 0 and Q becomes equal to equilibrium constant. Hence the above equation becomes,
∆G° = RT in Keq …………(2)
This equation is known as Van’t Hoff equation.
∆G° = – 2.303 RT log Keq ……….(3)
We also know that,
∆G° = ∆H°- T∆S° = – RT in Keq ……….(4)