Students can Download Maths Chapter 3 Algebra Intext Questions and Answers, Notes Pdf, Samacheer Kalvi 8th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 8th Maths Solutions Term 1 Chapter 3 Algebra Intext Questions
Exercise 3.1
Recap Page No. 66 and 67
Question 1.
Write the numbers of terms in the following expressions.
(i) x + y + z – xyz
Solution:
4 terms
(ii) m2n2c
Solution:
1 term
(iii) a2b2c – ab2c2 + a2bc2 + 3abc
Solution:
4 terms
(iv) 8x2 – 4xy + 7xy2
Solution:
3 terms
![]()
Question 2.
Identify the numerical co-efficient of each term in the following expressions.
Question 1.
2x2 – 5xy + 6y2 + 7x – 10y + 9
Solution:
Numerical co efficient in 2x2 is 2
Numerical co efficient in -5xy is -5
Numerical co efficient in 6y2 is 6
Numerical co efficient in 7x is 7
Numerical co efficient in -10y is – 10
Numerical co-efficient in 9 is 9
![]()
Question 2.
\(\frac{x}{3}+\frac{2 y}{5}-x y+7\)
Solution:

Numerical co efficient in -xy is -1
Numerical co efficient in 7 is 7
![]()
Question 3.
Pick out the like terms from the following.
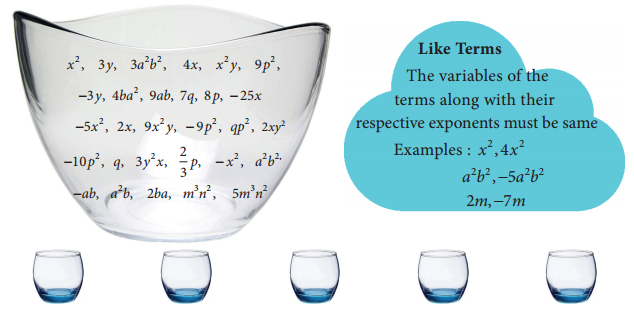
Solution:

Question 4.
Add : 2x, 6y, 9x – 2y
Solution:
2x + 6y + 9x – 2y = 2x + 9x + 6y – 2y = (2 + 9)x + (6 – 2)y = 11x + 4y
Question 5.
Simplify : (5x3 y3 – 3x2 y2 + xy + 7) + (2xy + x3y3 – 5 + 2x2y2)
Solution:
(5x3y3 – 3x2y2 + xy + 7) + (2xy + x3y3 – 5 + 2x2y2)
= 5x3y3 + x3y3 – 3x2y2 + 2x2y2 + xy + 2xy + 7 – 5
= (5 + 1)x3y3 + (-3 + 2)x2y2 +(1 +2)xy + 2
= 6x3y3 – x2y2 + 3xy + 2
![]()
Question 6.
The sides of a triangle are 2x – 5y + 9, 3y + 6x – 7 and -4x + y +10 . Find perimeter of the triangle.
Solution:
Perimeter of the triangle = Sum of three sides
= (2x – 5y + 9) + (3y + 6x – 7) + (-4x + y + 10)
= 2x – 5y + 9 + 3y + 6x – 7 – 4x + y + 10
= 2x + 6x – 4x – 5y + 3y + y + 9 – 7 + 10
= (2 + 6 – 4)x + (-5 + 3 + 1)y + (9 – 7 + 10)
= 4x – y + 12
∴ Perimeter of the triangle = 4x – y + 12 units.
Question 7.
Subtract -2mn from 6mn.
Solution:
6 mn – (-2mn) = 6mn + (+2mn) = (6 + 2) mn = 8mn
![]()
Question 8.
Subtract 6a2 – 5ab + 3b2 from 4a2 – 3ab + b2.
Solution:
(4a2 – 3ab+ b2) – (6a2– 5ab + 3b2)
= (4a2 – 6a2) + (- 3ab -(-5 ab)] + (b2– 3b2)
= (4 – 6) a2 + [-3ab + (+ 5ab)] + (1 – 3) b2
= [4 + (- 6)] a2 + (-3 + 5) ab + [1+ (-3)]b2
= -2a2 + 2ab – 2b2
![]()
Question 9.
The length of a log is 3a + 4b – 2 and a piece (2a – b) is remove from it. What is the length of the remaining log?
Solution:
Length of the log = 3a + 4b – 2

Length of the piece removed = 2a – b
Remaining length of the log = (3a + 4b – 2) – (2a – b)
= (3a – 2a) + [4b – (-b)] – 2
= (3 – 2)a + (4 + 1)b – 2
= a + 5b – 2
![]()
Question 10.
A tin had ‘x’ litre oil. Another tin had (3x2 + 6x – 5) litre of oil. The shopkeeper added (x + 7) litre more to the second tin. Later he sold (x2 + 6) litres of oil from the second tin. How much oil was left In the second tin?
Solution:
Quantity of oil in the second tin = 3x2 + 6x – 5 litres.
Quantity of oil added = x + 7 litres
∴ Total quantity of oil in the second tin
= (3x2 + 6x – 5) + (x + 7) litres
= 3x2 + (6x + x) + (-5 + 7)
= 3x2 + (6 + 1)x + 2
= 3x2 + 7x + 2 litres
Quantity of oil sold = x + 6 litres
∴ Quantity of oil left in the second tin = (3x2 + 7x + 2) – (x2 + 6)(3x2 – x2 ) + 7x + (2 – 6)
= (3 – 1)x2 + 7x + (-4) = 2x2 + 7x – 4
Quantity of oil left = 2x2 + 7x – 4 litres
Try this Page No. 70
Question 1.
Every algebraic expression is a polynomial. Is this statement true? Why?
Solution:
No, This statement is not true. Because Polynomials contain only whole numbers as the powers of their variables. But an algebraic expression may contains fractions and negative powers on their variables.
Eg. 2y2 + 5y-1 – 3 is a an algebraic expression. But not a polynomial.
Try this Page No. 71
Question 2.
-(5y2 + 2y – 6) Is this correct? If not, correct the mistake.
Solution:
Taking -(5y2 + 2y – 6) = 5y2 + [(-)(+) 2y] + [(-) × (-)6]
= -5y2 – 2y + 6
≠ -5y2 – 2y + 6
∴ Correct answer is -5y2 + 2y – 6 = -(5y2 + 2y + 6)
![]()
Try this Page No 71
(i) 3ab2, -2a2b3
(ii) 4xy, 5y2x, (-x2)
(iii) 2m, -5n, -3p
Solution:
(i) (3ab2) × (-2a2b2) = (+) × (-) × (3 × 2) × (a × a2) × (b2 × b3) = -6a3 b5
(ii) (4xy) × (5y2x) × (-x2)
= (+) × (+) × (-) × (4 × 5 × 1) × (x × x × x2) × (y × y2)
= -20x4y3
(iii) (2m) × (-5n) × (-3p) = (+) × (-) × (-) × (2 × 5 × 3) × m × n × p
= + 30mnp = 30 mnp
Try this Page No. 71
Question 1.
Why 3 + (4x – 7y) ≠ 12x – 21y?
Solution:
Addition and multiplication are different
3 + (4x – 7y) = 3 + 4x – 7y
We can add only like terms.
![]()
Try this Page No. 72
Question 1.
Which is corrcet? (3a)2 is equal to
(i) 3a2
(ii) 32a
(iii) 6a2
(iv) 9a2
Solution:
(3a) =32a2 = 9a2
(iv) 9a2 is the correct answer
Try These Page No.72
Question 1.
Multiply
(i) (5x2 + 7x – 3) by 4x2
Solution:
(5x2 + 7x – 3) × 4x2
= 4x2(5x2 + 7x – 3) Multiplication is commutative
= 4x2 (5x2 + 4x2 (7x) + 4x2 (-3)
= (4 × 5)(x2 × x2) + (4 × 7)(x2 × x) + (4 × -3)(x2)
= 20x4 + 28x3 – 12x2
(ii) (10x – 7y + 5z) by 6xyz
Solution:
(10x – 7y + 5z) by 6xyz
(10x – 7y + 5z) × 6xyz = 6xyz (10x – 7y + 5z) [∵ Multiplication is commutative]
= 6xy (10x) + 6xyz (-7y) + 6xyz (5z)
= (6 × 10)(x × x × y × z) + (6 × -7) + (x × y × y × z) + (6 × 5)(x × y × z × z)
= 60x2yz + (-42xy2z) + 30xyz2
= 60x2yz – 42x2z + 30xyz2
(iii) (ab + 3bc – 5ca) by – 3abc
Solution:
(ab + 3bc – 5ca) × (- 3abc) = (-3abc) (ab + 3bc – 5ca)
[∵ Multiplication is commutativel
= (-3abc) (ab) + (-3abc) (3bc) + (-3abc) (5ca)
= (-3)(a × a × b × b × c) + (- 3 × 3) + (a × b × b × c × c)
= -3a2b2c – 9ab2c2 – 30a2bc2
![]()
Try these Page No. 74
Question 1.
Multiply
(i) (a – 5) and (a + 4)
Solution:
(a – 5) (a + 4) = a(a + 4) – 5 (a + 4)
= (a × a) + (a × 4) + (-5 × a) + (-5 × 4)
= a2 + 4a – 5a – 20 = a2 – a – 20
(ii) (a + b) and (a – b)
Solution:
(a + b) (a – b) = a(a – b) + b (a – b)
= (a × a) + (a × -b)+(b × a) + b(-b)
= a2 – ab + ab – b2 = a2 – b2
(iii) (m4 + n4) and (m – n)
Solution:
(m4 + n4)(m – n) = m4(m – n) + n4(m – n)
= (m4 × m) + (m4 × (-n)) + (n4 × m (n4 × (-n))
= m5 – m4n + mn4 – n5
(iv) (2x + 3)(x – 4)
Solution:
(2x + 3)(x – 4) = 2x(x – 4) + 3(x – 4)
= (2x2 × x) – (2x × 4) + (3 × x) – (3 × 4)
= 2x2 – 8x + 3x – 12 = 2x2 – 5x – 12
(v) (x – 5)(3x + 7)
Solution:
(x – 5)(3x + 7) = x(3x + 7) – 5(3x + 7)
= (x × 3x) + (x × 7) + (-5 × 3x) + (-5 × 7)
= 3x2 + 7x – 15x – 35
= 3x2 – 8x – 35
(vi) (x – 2)(6x – 3)
Solution:
(x – 2)(6x – 3) × (6x – 3) – 2(6x – 3)
= (x × 6x)+(x × (-3) × (2 × 6x) – (2 × 3)
= 6x2 – 3x – 12x + 6
= 6x2 – 15x + 6
Try this Page No. 74
Question 2.
3x2 (x4 – 7x3 + 2), what is the highest power in the expression.
Solution:
3x2(x4 – 7x3 + 2) = (3x2) (x4) + 3x2 (-7x3)+ (3x2)2
= 3x6 – 21x5 + 6x2
Highest power is 6 in x6.
![]()
Exercise 3.2
Try this Page No. 77
Question 1.
Are the following correct?
(i) \(\frac{x^{3}}{x^{8}}=x^{8-3}=x^{5}\)
(ii) \(\frac{10 m^{4}}{10 m^{4}}=0\)
(iii) When a monomial is divided by itself, we will get I?
Solution:

Try this Page No. 77
Question 1.
Divide
![]()
Solution:
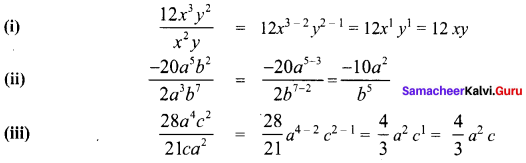
Try this Page No. 78
Question 1.
Are the following divisions correct ?

Solution:

Try this Page No. 78
Question 1.

Solution:
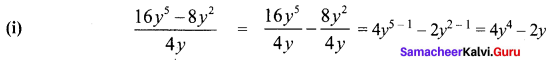
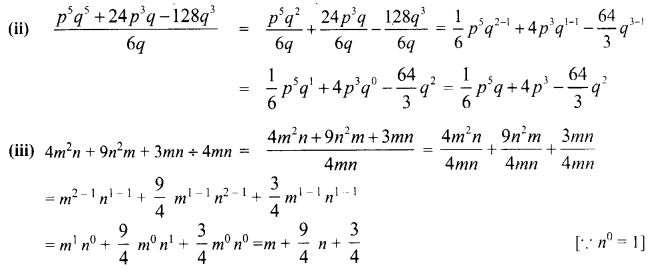
Exercise 3.3
Try these Page No. 81
Question 1.
1. (p + 2)2 = …….
2. (3 – a)2 = …….
3. (62 – x2) = ………
4. (a + b)2 – (a – b)2 = …….
= a2 + 2ab + b2 – a2 – 2ab – b2
= (1 – 1)a2 + (2 + 2)ab + (+1 – 1 )b2 = 4ab
5. (a + b)2 = (a + b) × (a + b)
6. (m + n)( m – n) = m2 – n2
7. (m + 7)2 = m2 + 14m + 49
8. (k2 – 36) ≡ k2 – 62 = (k + 6)(k – 6)
9. m2 – 6m + 9 = (m – 3)2
10. (m – 10)(m + 5) = m2 + (-10 + 5)m + (-10)(5) = m2 – 5m – 50
Solution:

![]()
Try these page No. 83
Question 1.
Expand using appropriate identities
Question 1.
(3p + 2q)2
Solution:
(3p + 2q)2
Comparing (3p + 2q)2 with (a + b)2, we get a = 3p and b = 2q.
(a + b)2 = a2 + 2ab + b2
(3p + 2q)2 = (3p)2+ 2(3p) (2q) + (2q)2
= 9p2 + 12pq + 4q2
![]()
Question 2.
(105)2
Solution:
(105)2 = (100 + 5)2
Comparing (100 + 5)2 with (a + b)2, we get a = 100 and b = 5.
(a + b)2 = a2 + 2ab + b2
(100 + 5)2 = (100)2 + 2(100)(5) + 52 = 1oooo + 1000 + 25
1052 = 11,025
Question 3.
( 2x – 5d)2
Solution:
(2x – 5d)2
Comparing with (a – b)2, we get a = 2x b = 5d.
(a – b)2 = a2 – 2ab + b2
(2x – 5d)2 = (2x)2 – 2(2x)(5d) + (5d)2
= 2x2 – 20 xd + 52d2 = 4x2 – 20 xd + 25d2
![]()
Question 4.
(98)2
Solution:
(98)2 = (100 – 2)2
Comparing (100 – 2)2 with (a – b)2 we get
a = 100, b = 2
(a – b)2 = a2 – 2ab + b2
(100 – 2)2 = 1002 – 2(100)(2) + 22
= 10000 – 400 + 4 = 9600 + 4 = 9604
Question 5.
(y – 5)(y + 5)
Solution:
(y – 5)(y + 5)
Comparing (y – 5) (y + 5) with (a – b) (a + b) we get
a = y; b = 5
(a – b)(a + b) = a2 – b2
(y – 5)(y + 5) = y2 – 52 = y2 – 25
![]()
Question 6.
(3x)2 – 52
Solution:
(3x)2 – 52
Comparing (3x)2 – 52 with a2 – b2 we have
a = 3x; b = 5
(a2 – b2) = (a + b)(a – b)
(3x)2 – 52 = (3x + 5)(3x – 5) = 3x(3x – 5) + 5(3x – 5)
= (3x) (3x) – (3x)(5) + 5(3x) – 5(5)
= 9x2 – 15x + 15x – 25 = 9x2 – 25
Question 7.
(2m + n)(2m +p)
Solution:
(2m + n) (2m + p)
Comparing (2m + n) (2m + p) with (x + a) (x + b) we have
x = 2n; a = n ;b = p
(x – a)(x + b) = x2 + (a + b)x + ab
(2m +n) (2m +p) = (2m2) + (n +p)(2m) + (n) (p)
= 22m2 + n(2m) + p(2m) + np
= 4m2 + 2mn + 2mp + np
![]()
Question 8.
203 × 197
Solution:
203 × 197 = (200 + 3)(200 – 3)
Comparing (a + b) (a – b) we have
a = 200, b = 3
(a + b)(a – b) = a2 – b2
(200 + 3)(200 – 3) = 2002 – 32
203 × 197 = 40000 – 9
203 × 197 = 39991
Question 9.
Find the area of the square whose side is (x – 2)
Solution:
Side of a square = x – 2
∴ Area = Side × Side
= (x – 2) (x – 2) = x(x – 2) – 2(x – 2)
= x(x) + (x)(-2) + (-2)(x) + (-2)(-2)
= x – 2x – 2x + 4x2 – 4x + 4
![]()
Question 10.
Find the area of the rectangle whose length and breadth are (y + 4) and (y – 3).
Solution:
Length of the rectangle = y+ 4
breadth of the rectangle = y – 3
Area of the rectangle = length × breadth
= (y + 4)(y – 3) = y2 + (4 +(-3))y + (4)(-3)
= y2 + y – 12
Try these Page No. 88
Question 1.
Expand :
Question 1.
(x + 4)3
Solution:
Comparing (x + 4)3 with (a + b)3, we have a = x and b = 4.
(a + b)3 = a3 + 3a2b + 3ab2 + b3
(x + 4)3 = x3 + 3x2(4) + 3(x)(4)2 + 43
= x3 + 12x2 + 48x + 64
![]()
Question 2.
( y – 2)2
Solution:
Comparing (y – 2) with (a – b)3 we have a = y b = z
(a – b)3 = a3 – 3a2b + 3ab2 – b3
(y – 2)2 = y3 – 3y(2) + 3y(2)2 + 23
= y3 – 6y2 + 12y + 8
Question 3.
(x + 1)(x + 3)(x + 5)
Solution:
Comparing (x + 1) (x + 3) (x + 5) with (x + a) (x + b) (x + c) we have
a = 1
b = 3
and c = 5
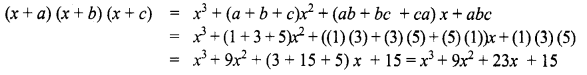
Exercise 3.4
Try These Page No.92
Question 1.
Factorize the following:
Question 1.
3y + 6
Solution:
3y + 6
3y + 6 = 3 × y + 2 × 3
Taking out the common factor 3 from each term we get 3 (y + 2)
∴ 3y + 6 = 3(y + 2)
![]()
Question 2.
10x2 + 15y
Solution:
10x2 + 15y2
10x2 + 15y2 = (2 × 5 × x × x) + (3 × 5 × y × y)
Taking out the common factor 5 we have
10x2 + 15y2 = 5(2x2 + 3y2)
Question 3.
7m(m – 5) + 1(5 – m)
Solution:
7m(m – 5) + 1(5 – m)
7m(m – 5) + 1(5 – m) = 7m(m – 5) + (-1)(-5 + m)
= 7m(m – 5) – 1 (m – 5)
Taking out the common binomial factor (m – 5) = (m – 5)(7m – 1)
![]()
Question 4.
64 – x2
Solution:
64 – x2
64 – x2 = 82 – x2
This is of the form a2 – b2
Comparing with a2 – b2 we have a = 8, b = x
a2 – b2 = (a + b)(a – b)
64 – x2 = (8 + x)(8 – x)