You can Download Samacheer Kalvi 9th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 3 Algebra Additional Questions
Exercise 3.1
Question 1.
Classify the following polynomials based on number of terms.
(i) x3 – x2
(ii) 5x
(iii) 4x4 + 2x3 + 1
(iv) 4.x3
(v) x + 2
(vi) 3x2
(vii) y4 + 1
(viii) y20 + y18 + y2
(ix) 6
(x) 2u3 + u2 + 3
(xi) u23 – u4
(xii) y
Solution:
5x, 3x2, 4x3, y and 6 are monomials because they have only one term.
x3 – x2, x + 2, y4 + 1 and u23 – u4 are binomials as they contain only two terms.
4x4 + 2x3 + 1 , y20 + y18 + y2 and 2u3 + u2 + 3 are trinomials as they contain only three terms.
Question 2.
Classify the following polynomials based on their degree.
Solution:
p(x) = 3, p(x) = -7, p(x) = \(\frac{3}{2}\) are constant polynomials
p(x) = x + 3, p(x) = 4x, p(x) = \(\sqrt{3}\)x + 1 are linear polynomials, since the highest degree of the variable x is one.
p(x) = 5x2 – 3x + 2, p(y) = \(\frac{5}{2}\) y2 + 1, p(x) = 3x2 are quadratic polynomials, since the highest degree of the variable is two.
p(x) = 2x3 – x2 + 4x + 1, p(x) = x3 + 1, p(y) = y3 + 3y are cubic polynomials, since the highest degree of the variable is three.
Question 3.
Find the product of given polynomials p(x) = 3x3+ 2x – x2 + 8 and q (x) = 7x + 2.
![]()
Solution:
(7x +2) (3x3 + 2x – x2 + 8) = 7x(3x3 + 2x – x2 + 8) + 2x
(3x3 + 2x – x2 + 8) = 21x4 + 14x2 – 7x3 + 56x + 6x3 + 4x – 2x2+ 16 = 21x4 – x3 + 12x4 + 60x + 16
Question 4.
Let P(x) = 4x4 – 3x + 2x3 + 5 and q(x) = x2 + 2x + 4 find p (x) – q(x).
Solution:

Exercise 3.2
Question 1.
If p(x) = 5x3 – 3x2 + 7x – 9, find
(i) p(-1)
(ii) p(2).
Solution:
Given that p(x) = 5x3 – 3x2 + 7x – 9
(i) p(-1) = 5(-1)3 – 3(-1)2 + 7(-1) – 9 = -5 – 3 – 7 – 9
= -24
(ii) p(2) = 5(2)3 – 3(2)3 + 7(2) – 9 = 40 – 12 + 14 – 9
∴ p(2) = 33
Question 2.
Find the zeros of the following polynomials.
(i) p(x) = 2x – 3
(ii) p(x) = x – 2
Solution:

Exercise 3.3
Question 1.
Find the remainder using remainder theorem, when
(i) 4x3 – 5x2 + 6x – 2 is divided by x – 1.
(ii) x3 – 7x2 – x + 6 is divided by x + 2.
Solution:
(i) Let p(x) = 4x3 – 5x2 + 6x – 2. The zero of (x – 1) is 1.
When p(x) is divided by (x – 1) the remainder is p( 1). Now,
p(1) = 4(1)3 – 5(1)2 + 6(1) – 2 = 4 – 5 + 6 – 2 = 3
∴ The remainder is 3.
(ii) Let p(x) = x3 – 7x2 – x + 6. The zero of x + 2 is -2.
When p(x) is divided by x + 2, the remainder is p(-2). Now,
p(-2) = (-2)3 – 7(-2)2 – (-2) +6 = – 8 – 7(4) + 2 + 6
= – 8 – 28 + 2 + 6 = -28.
∴ The remainder is -28.
Question 2.
Find the value of a if 2x3 – 6x2 + 5ax – 9 leaves the remainder 13 when it is divided by x – 2.
Solution:
Let p(x) = 2x3 – 6x2 + 5ax – 9
When p(x) is divided by (x – 2) the remainder is p(2).
Given that p(2) = 13
⇒ 2(2)3 – 6(2)2 + 5a(2) – 9 = 13
⇒ 2(8) – 6(4) + 10a – 9 = 13
⇒ 16 – 24 + 10a – 9 = 13
⇒ 10a – 17 = 13
⇒ 10a = 30
⇒ ∴ a = 3
![]()
Question 3.
If the polynomials f(x) = ax3+ 4x2 + 3x – 4 and g (x) = x3 – 4x + a leave the same remainder when divided by x – 3. Find the value of a. Also find the remainder.
![]()
Solution:
Let f(x) = ax3 + 4x2 + 3x – 4 and g(x) = x3 – 4x + a,When f(x) is divided by (x – 3), the remainder is f(3).
Now f(3) = a(3)34(3)2 + 3(3) – 4 = 27a + 36 + 9 – 4
f (3) = 27a + 41 …(1)
When g(x) is divided by (x – 3), the remainder is g(3).
Now g(3) = 33 – 4(3) + a = 27 – 12 + a = 15 + a …(2)
Since the remainders are same, (1) = (2)
Given that, f(3) = g(3)
That is 27a + 41 = 15 +a
27a – a = 15 – 41
26a = -26
![]()
Sustituting a = -1, in f(3), we get
f(3) = 27(-1) + 41 = -27 + 41
f(3) = 14
∴ The remainder is 14.
Question 4.
Show that x + 4 is a factor of x3 + 6x2 – 7x – 60.
Solution:
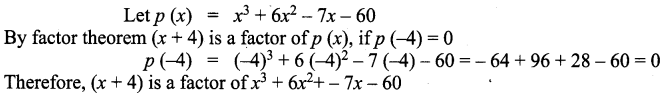
Question 5.
In (5x + 4) a factor of 5x3 + 14x2 – 32x – 32
Solution:
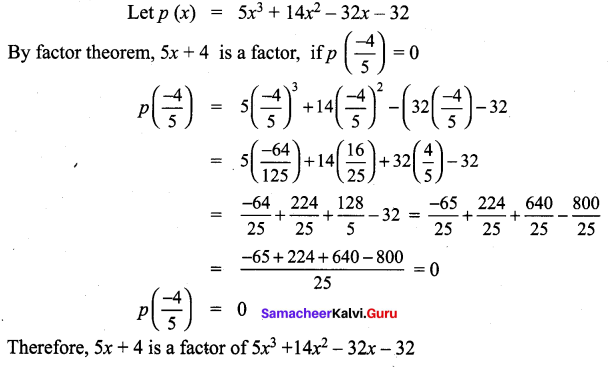
Question 6.
Find the value of k, if (x – 3) is a factor of polynomial x3 – 9x2 + 26x + k.
Solution:
Let p (x) = x3 – 9x2 + 26x + k
By factor theorem, (x – 3) is a factor of p(x), if p(3) = 0
p(3) = 0
33 – 9(3)2 + 26 (3) + k = 0
27 – 81 + 78 + k = 0
k = -24

Question 7.
Show that (x – 3) is a factor of x3 + 9x2 – x – 105.
Solution:
Let p(x) = x3 + 9x2 – x – 105
By factor theorem, x – 3 is a factor of p(x), if p(3) = 0
p (3) = 33 + 9(3)3 – 3 – 105
= 27 + 81 – 3 – 105
= 108 – 108
p(3) = 0

Therefore, x – 3 is a factor of x3 + 9x2 – x – 105.
Question 8.
Show that (x + 2) is a factor of x3 – 4x2 – 2x + 20.
Solution:
Let p(x) = x3 – 4x2 – 2x + 20
By factor theorem,
(x + 2) is factor of p(x), if p(-2) = 0
p(-2) = (-2)3 – 4(-2)2 – 2(-2) + 20 = -8 – 4(4) + 4 + 20
P(- 2) = 0
Therefore, (x + 2) is a factor of x3 – 4x2 – 2x + 20
Exercise 3.4
Question 1.
Expand the following using identities :
(i) (7x + 2y)2
(ii) (4m – 3m)2
(iii) (4a + 3b) (4a – 3b)
(iv) (k + 2)(k – 3)
Solution:
(i) (7x + 2y)2 = (7x)2 + 2 (7x) (2y) + (2y)2 = 49x2 + 28xy + 4y2
(ii) (4m – 3m)2 = (4m)2 – 2(4m) (3m) + (3m)2 = 16m2 – 24mn + 9n2
(iii) (4a + 3b) (4a – 3b) [We have (a + b ) (a – b) = a2 – b2 ]
Put [a = 4a, b = 3b]
(4a + 3b) (4a – 3b) = (4a)2 – (3b)2 = 16a2 – 9b2
(iv) (k + 2)(k – 3) [We have (x + a) (x – b) = x2 + (a – b)x – ab]
Put [x = k, a = 2, b = 3]
(k + 2) (k – 3) = k2 + (2 – 3)x – 2 × 3 = k2 – x – 6
Question 2.
Expand : (a + b – c)2
Solution:
Replacing ‘c’ by ‘-c’ in the expansion of
(a + b + c)2 = a2 + b2 + c2 + 2 ab+ 2 bc + 2ca
(a + b + (-c))2 = a2 + b2 + (-c)2 + 2ab + 2b(-c) + 2(-c)a
= a2 + b2 + c2 + 2ab – 2bc – 2ca
Question 3.
Expand : (x + 2y + 3z)2
Solution:
We know that,
(a + b + c)2 = a2 + b2 + c2 + 2ab + 2bc + 2ca
Substituting, a = x, b = 2y and c = 3z
(x + 2y + 3 z)2 = x2 + (2y)2 + (3z)2 + 2(x)(2y) + 2(2y)(3z) + 2(3z)(x)
= x2 + 4y2 + 9z2 + 4xy + 12y2 + 6zx
Question 4.
Find the area of square whose side length is m + n – q.
Solution:
Area of square = side × side = (m + n – q)2
We know that,
(a + b + c)2 = a2 + b2 + c2 + 2ab + 2bc + 2ca
[m + n + (-q)]2 = m2 + n2 + (-q)2 + 2mn + 2n(-q) + 2(-q)m
= m2 + n2 + q2 + 2mn – 2nq – 2qm
Therefore, Area of square = m2 + n2 + q2 + 2mn – 2nq – 2qm = [m2 + n2 + q2 + 2mn – 2nq – 2qm] sq. units.
![]()
EXERCISE 3.5
Question 1.
Factorise the following
(i) 25m-2 – 16n2
(ii) x4 – 9x2
Solution:
(i) 25m2 – 16n2 = (5m)2 – (4n)2
= (5m – 4n) (5m + 4n) [∵ a2 – b2 = (a – b)(a + b)]
(ii) x4 – 9x2 = x2(x2 – 9) = x2(x2 – 32) = x2(x – 3)(x + 3)
Question 2.
Factorise the following.
(i) 64m3 + 27n3
(ii) 729x3 – 343y3
Solution:
(i) 64m3 + 27n3 = (4m)3 + (3n)3
= (4m + 3n) ((4m)2 – (4m) (3n) + (3n)2) [∵ a2 + b2 = (a + b) (a2 – ab + b2)]
= (4m + 3n) (16m2 – 12mn + 9n2)
(ii) 729x3 – 343y3 = (9x)3 – (7y)3 = (9x – 7y) ((9x)2 + (9x) (7y) + (7y)2
= (9x – 7y) (81x2 + 63xy + 49y2)
[∵ a3 – b3 = (a – b) (a2 + ab + b2)]
Question 3.
Factorise 81x2 + 90x + 25
Solution:
81x2 + 90x + 25 = (9x)2 + 2 (9x) (5) + 52
= (9x + 5)2 [ ∵ a2 + 2ab + b2 = (a + b)2]
Question 4.
Find a3 + b2 if a + b = 6, ab = 5.
Solution:
Given, a + b = 6, ab = 5
a2 + b2 = (a + b)2 – 3ab(a + b) = (6)3 – 3(5)(6) = 126
Question 5.
Factorise (a – b)2 + 7(a – b) + 10
Solution:
Let a – b = p, we get p2 + 7p + 10,
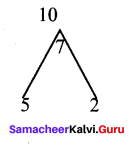
p2 + 7p + 10 = p2 + 5p + 2p + 10
= p(p + 5) + 2(p + 5) = (p + 5)(p + 2)
Put p = a – b we get,
(a – b)2 + 7(a – b) + 10 = (a – b + 5)(a – b + 2)
Question 6.
Factorise 6x2 + 17x + 12
Solution:
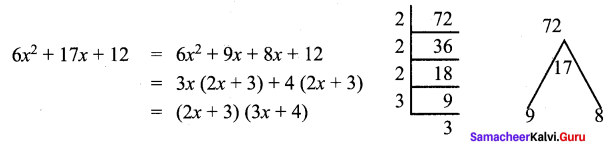
Exercise 3.6
Question 1.
Factorise x2 + 4x – 96
Solution:
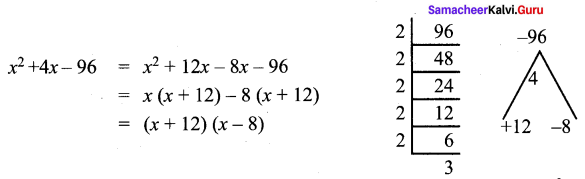
Question 2.
Factorise x2 + 7xy – 12y2
Solution:
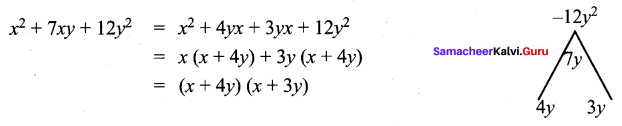
Question 3.
Find the quotient and remainder when 5x3 – 9x2 + 10x + 2 is divided by x + 2 using synthetic division.
Solution:

Hence the quotient is 5x2 – 19x + 48 and remainder is -94.
Question 4.
Find the quotient and remainder when -7 + 3x – 2x2 + 5x3 is divided by -1 + 4x using synthetic division.
Solution:
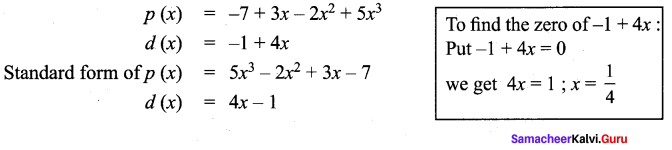

Question 5.
If the quotient on dividing 5x4 + 4x3 + 2x + 1 by x + 3 is 5x3 + 9x2 + bx – 97 then find the values of a, b and also remainder.
Solution:
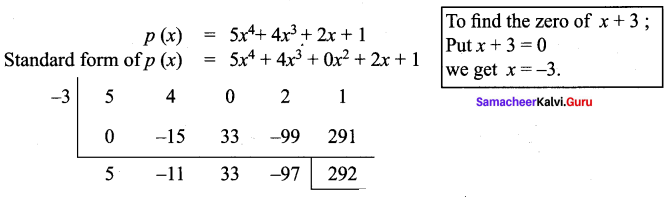
Quotient 5x3 + 11x2 + 33x – 97 is compared with given quotient 5x3 + ax2 + bx – 97
co-efficient of x2 is – 11 = a and co-efficient of x is 33 = b.
Therefore a = -11, b = 33 and remainder = 292.
Exercise 3.7
Question 1.
Find the quotient and the remainder when 10 – 4x + 3x2 is divided by x – 2.
Solution:
Let us first write the terms of each polynomial in descending order (or ascending
order). Thus the given problem becomes (3x2 – 4x + 10) ÷ (x – 2)
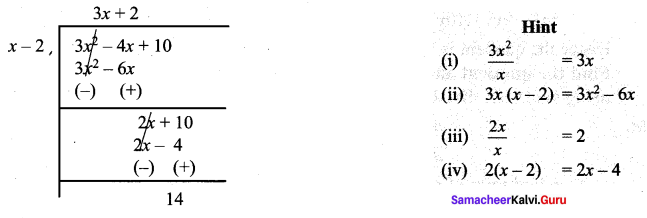
∴ Quotient = 3x + 2 and Remainder = 14, i.e 3x2 – 4x + 10 = (x – 2) (3x + 2) + 14 and is in the form
Dividend = (Divisor × Quotient) + Remainder
Question 2.
If 8x3 – 14x2 – 19x – 8 is divided by 4x + 3 then find the quotient and the remainder.
Solution:

Exercise 3.8
Question 1.
Factorise 2x3 – x2 – 12x – 9 into linear factors.
Solution:
Let p(x) = 2x3 – x2 – 12x – 9
Sum of the co-efficients = 2 – 1 – 12 – 9 = -20 ≠ 0
Hence x – 1 is not a factor
Sum of co-efficients of even powers with constant = -1 – 9 = -10
Sum of co-efficients of odd powers = 2 – 12 = -10
Hence x + 1 is a factor of x.
Now we use synthetic division to find the other factors.
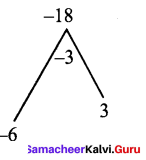
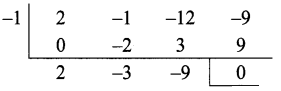
Then p (x) = (x + 1)(2x2 – 3x – 9)
Now 2x2 – 3x – 9 = 2x2 – 6x + 3x – 9 = 2x(x – 3) + 3(x – 3)
= (x – 3)(2x + 3)
Hence 2x3 – x2 – 12x – 9 = (x + 1) (x – 3) (2x + 3)
Question 2.
Factorize x3 + 3x2 – 13x – 15.
Solution:
Let p(x) = x3 + 3x2 – 13x – 15
Sum of all the co-efficients = 1 + 3 – 13 – 15 = -24 + 0
Hence x – 1 is not a factor
Sum of co-efficients of even powers with constant = 3 – 15 = – 12
Sum of coefficients of odd powers = 1 – 13 = – 12
Hence x + 1 is a factor of p (x)
Now use synthetic division to find the other factors.
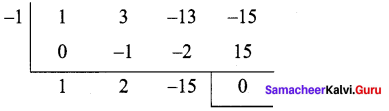
Hence p(x) = (x + 1) (x2 + 2x – 15)
Now x3 + 3x2 – 13x – 15 = (x + 1)(x2 + 2x – 15)
Now x2 + 2x – 15 = x2 + 5x – 3x – 15 = x(x + 5) – 3 (x + 5) = (x + 5)(x – 3)
Hence x3 + 3x2 – 13x – 15 = (x + 1)(x + 5)(x – 3)
Question 3.
Factorize x3 + 13x2 + 32x + 20 into linear factors.
![]()
Solution:
Let, p(x) = x3 + 13x2 + 32x + 20
Sum of all the coefficients = 1 + 13 + 32 + 20 = 66 ≠ 0
Hence, (x – 1) is not a factor.
Sum of coefficients of even powers with constant = 13 + 20 = 33
Sum of coefficients of odd powers = 1 + 32 = 33
Hence, (x + 1) is a factor of p(x)
Now we use synthetic division to find the other factors

Exercise 3.9
Question 1.
Find GCD of 25x3y2 z, 45x2y4z3b
Solution:
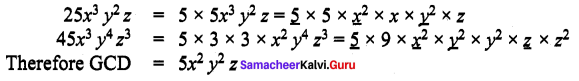
Question 2.
Find the GCD of (y3 – 1) and (y – 1).
Solution:
y3 – 1 = (y – 1)(y3 + y + 1)
y – 1 = y – 1
Therefore, GCD = y – 1
Question 3.
Find the GCD of 3x2 – 48 and x2 – 7x + 12.
Solution:
3x2 – 48 = 3(x2 – 16) = 3(x2 – 43) = 3(x + 4)(x – 4)
x2 – 7x + 12 = x2 – 3x – 4x + 12 = x(x – 3) – 4 (x – 3) = (x – 3) (x – 4)
Therefore, GCD = x – 4
Question 4.
Find the GCD of ax , ax + y, ax + y + z.
Solution:

Exercise 3.10
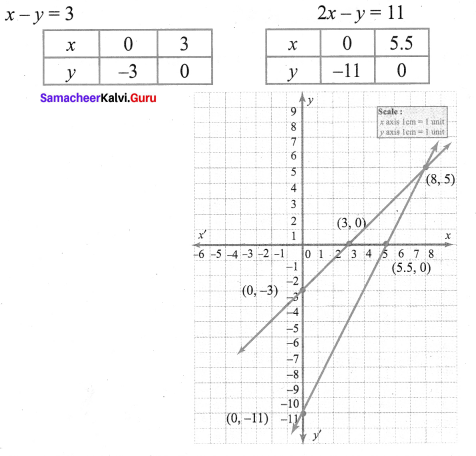
Question 5.
Solve graphically. x – y = 3 ; 2x – y = 11
Solution:
Exercise 3.11
Question 1.
Solve using the method of substitution. 5x – y = 5, 3x + y = 11
Solution:
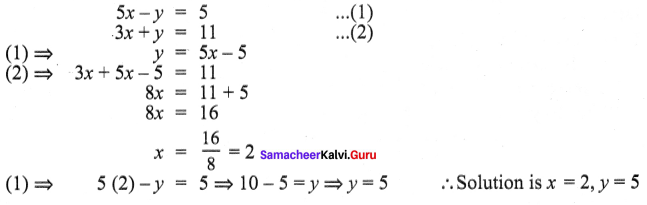
Exercise 3.12
Question 2.
Solve by the method of elimination. 2x + y = 10; 5x – y = 11
Solution:

Exercise 3.13
Question 3.
Solve 5x – 2y = 10 ; 3x + y = 17 by the method of cross multiplication.
Solution:
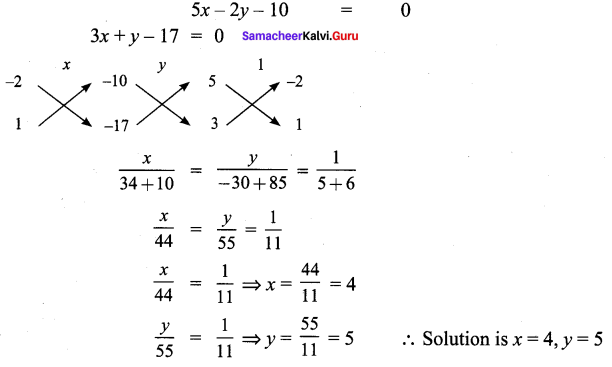
Exercise 3.14
Question 1.
The age of Arjun is twice the sum of the ages of his two children. After 20 years, his age will be equal to the sum of the ages of his children. Find the age of the father.
Solution:
Let the age of the father be x
Let the sum of the age of his sons be y
At present x = 2y ⇒ x – 2y = 0 …. (1)
After 20 years x + 20 = y + 40
x – y = 40 – 20
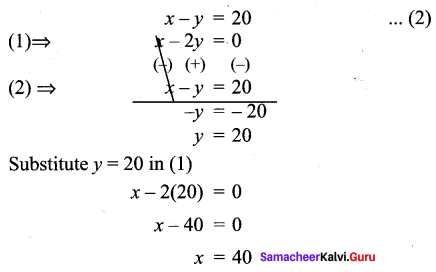
Exercise 3.15
Multiple Choice Questions :
Question 1.
The polynomial 3x – 2 is a
(1) linear polynomial
(2) quadratic polynomial
(3) cubic polynomial
(4) constant polynomial
Hint: A polynomial is linear if its degree is 1
Solution:
(1) linear polynomial
Question 2.
The polynomial 4x2 + 2x – 2 is a
(1) linear polynomial
(2) quadratic polynomial
(3) cubic polynomial
(4) constant polynomial
Hint: A polynomial is quadratic of its highest power of x is 2
Solution:
(2) quadratic polynomial]
Question 3.
The zero of the polynomial 2x – 5 is

Hint:
![]()
Solution:
(1) \(\frac{5}{2}\)
Question 4.
The root of the polynomial equation 3x – 1 = 0 is
![]()
Hint:
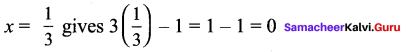
Solution:
(2) x = \(\frac{1}{3}\)
Question 5.
Zero of (7 + 4x) is ___

Solution:
(2) \(\frac{-7}{4}\)
Question 6.
Which of the following has as a factor?
(1) x2 + 2x
(2) (x – 1)2
(3) (x + 1)2
(4) (x2 – 22)
Solution:
(1) x2 + 2x
Question 7.
If x – 2 is a factor of q (x), then the remainder is _____
(1) q (-2)
(2) x – 2
(3) 0
(4) -2
Solution:
(3) 0
Question 8.
(a – b) (a2 + ab + b2) =
Solution:
(1) a3 + b3 + c3 – 3abc
(2) a2 – b2
(3) a3 + b3
(4) a3 – b3
Solution:
(4) a3 – b3
Question 9.
The polynomial whose factors are (x + 2) (x + 3) is
(1) x2 + 5x + 6
(2) x2 – 4
(3) x2 – 9
(4) x2 + 6x + 5
Solution:
(1) x2 + 5x + 6
Question 10.
(-a – b – c)2 is equal to
(1) (a – b + c)2
(2) (a + b – c)2
(3) (-a + b + c)2
(4) (a + b + c)2
Solution:
(4) (a + b + c)2
Text Book Activities
Activity – 1
Write the Variable, Coefficient and Constant in the given algebraic expression,
Solution:
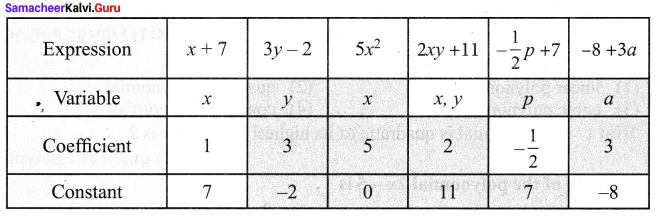
Activity – 2
Write the following polynomials in standard form.

Activity – 3
Question 1.
Find the value of k for the given system of linear equations satisfying the condition below:
(i) 2x + ky = 1; 3x – 5y = 7 has a unique solution
(ii) kx + 3y = 3; 12x + ky = 6 has no solution
(iii) (k – 3)x + 3y = k; kx + ky = 12 has infinite number of solution
Solution:
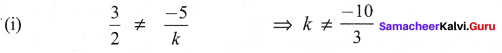
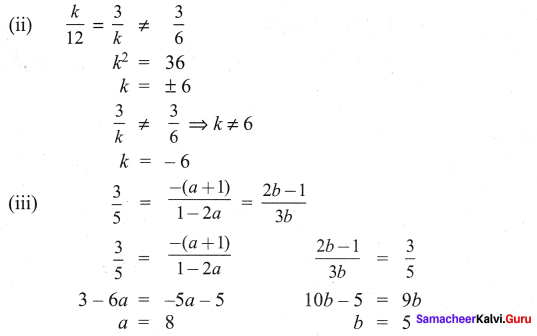
Question 2.
Find the value of a and b for which the given system of linear equation has infinite number of solutions 3x – (a + 1)y = 2b – 1, 5x + (1 – 2a)y = 3b
Solution:
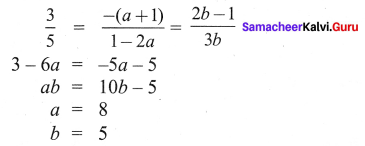
Activity – 4
For the given linear equations, find another linear equation satisfying each of the given condition
Solution:
