Students can Download Maths Chapter 2 Measurements Intext Questions and Answers, Notes Pdf, Samacheer Kalvi 7th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 7th Maths Solutions Term 1 Chapter 2 Measurements Intext Questions
Exercise 2.1
Parallelogram
(Try These Text book Page No. 33)
Question 1.
Find the missing values for the following:

Solution:
(i) Given length l = 12 m; Breadth b = 8 cm
∴ Area of rectangle = l × b sq. units = 12 × 8 m2 = 96 m2
Perimeter of the rectangle = 2 × (1 + b) units = 2 × (12 + 8)m = 2 × 20 = 40m
(ii) Given Length l = 15 cm ; Area of the rectangle = 90 sq. cm
l × b = 90; 15 × 6 = 90; b = \(\frac{90}{15}\) = 6 cm
Perimeter of the rectangle = 2 × (l+ b) units = 2 × (15 + 6) cm = 2 × 21 cm = 42 cm
(iii) Given Breadth of rectangle = 50 mm ; Perimeter of the rectangle = 300 mm
2 × (l + b) = 300
2 × (l + 50) = 300
l + 50 = \(\frac{300}{2}\) = 150
l = 150 – 50
l = 100
Area = l × b sq. untis = 100 × 50 mm2 = 5000 mm2
(iv) Length of the rectangle = 12 cm ; Perimeter = 44 cm
2(l + b) = 44
2(12 + b) = 44
12 + b = \(\frac{44}{2}\)
12 + b = 22 ; b = 22 – 12; b = 10 cm
Area = l × b sq. units
= 12 × 10 cm2 = 120 cm2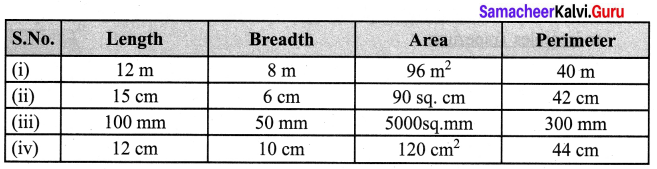
Question 2.

Solution:
(i) Given side a = 60 cm
Area of the square = a × a sq.units = 60 × 60 cm2 = 3600 cm2
Perimeter of the square = 4 × a units = 4 × 60 cm = 240 cm
(ii) Given area of a square = 64 sq. m
a × a = 64
a × a = 8 × 8
a = 8m
Perimeter = 4 × a
= 4 × 8
= 32 m
(iii) Given perimeter of the square = 100 mm
4 × a = 100
a = \(\frac{100}{4}\) mm
a = 25 mm
Area = a × a sq. units
= 25 × 25 mm2
= 625 mm2

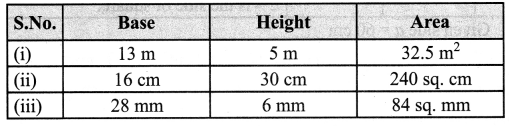
Question 3.

Solution:
(i) Given base of the right angled triangle = 13 m ; height = 5 m

(iii) Given height h = 6 mm ; Area = 84 sq. mm
\(\frac{1}{2}\) × b × h = 84 ; \(\frac{1}{2}\) × b × 6 = 84
b = \(\frac{{84} \times 2}{6}\); b = 28 mm
![]()
(Try This Textbook Page No. 35)
Question 1.
Explain the area of the parallelogram as sum of the areas of the two triangles.
Solution:
ABCD is a parallelogram. It can be divided into two triangles of equal area by drawing the diagonal BD.
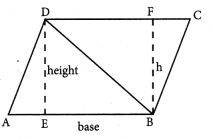
Area of the parallelogram ABCD = base × height
= AB × DE

Question 2.
A rectangle is a parallelogram but a parallelogram is not a rectangle. Why?
Solution:
(i) For both rectangle and parallelogram
(i) opposite sides are equal and parallel.
(ii) For rectangle all angles equal to 90°. But for parallelogram opposite angles are equal.
∴ All rectangles are parallelograms. But all parallelograms are not rectan¬gles as their angles need not be equal to 90°.
(Try These Textbook Page No. 36)
Question 1.
Count the squares and find the area of the following parallelograms by converting those into rectangles of the same area. (Without changing the base and height).
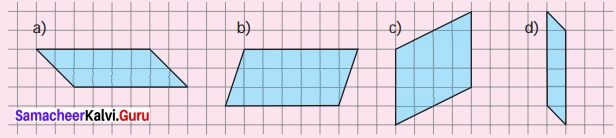
(a) ______ sq. units
(b) ______ sq. units
(c) ______ sq. units
(d) ______ sq. units
Solution:
Converting the given parallelograms into rectangles we get.
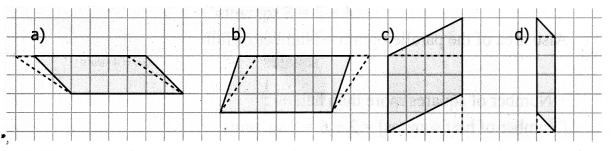
(a) 10 sq. units
(b) 18 sq. units
(c) 16 sq. units
(d) 5 sq. units
Question 2.
Draw the heights for the given parallelograms and mark the measure of their bases and find the area. Analyze your result.

Solution:
(a) Area of the parallelogram = b × h sq. units
= 4 × 2 sq. units = 8 sq. units

By counting the small squares also we get number of full
squares + number of square more than half = 6 + 2 = 8 sq. units.
(b) Area of the parallelogram = base × height = 4 × 2 = 8 sq. units
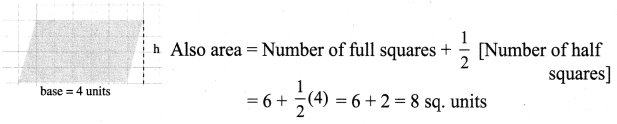
(c) Area of the parallelogram = base × height = 4 × 2 = 8 sq. units

Also area = Number of full squares + Number of squares more than half + \(\frac{1}{2}\) Number of half squares = 4 + 4 = 8 sq. units
(d) Area of the parallelogram = (base × height) sq. units = 4 × 2 sq. units = 8 sq. units
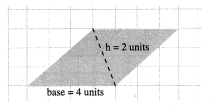
Also area of the parallelogram = Number of full squares + \(\frac{1}{2}\) [Number of half squares] + Number of squares more than half = 4 + 0 + 4 = 8sq. units
(e) Area of parallelogram = (base × height) sq. units
= 4 × 2 sq. units = 8 sq. units
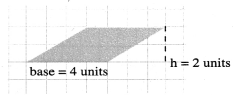
Also area of the parallelogram = Number of full squares + Number of squares more than half + \(\frac{1}{2}\) [Number of half squares] = 2 + 6 = 8sq. units
Question 3.
Find the area o the following parallelograms by measuring their base and height, using formula.
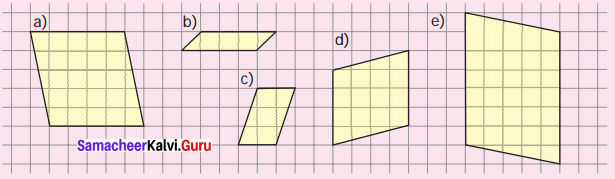
(a) _____ sq. units
(b) _____ sq. units
(c) _____ sq. units
(d) _____ sq. units
(e) _____ sq. units
Solution:
(a) Area of the rectangle = (base × height) sq. units
base = 5 units
height = 5 units
∴ Area = (5 × 5 ) = sq. units = 25 sq. units
(b) Area of the rectangle = (base × height) sq. units
base = 4 units
height = 1 units
∴ Area = (4 × 1 ) = sq. units = 4 sq. units
(c) Area of the rectangle = (base × height) sq. units
base = 2 units
height = 3 units
∴ Area = (2 × 3 ) = sq. units = 6 sq. units
(d) Area of the rectangle = (base × height) sq. units
base = 4 units
height = 4 units
∴ Area = (4 × 4 ) = sq. units = 16 sq. units
(e) Area of the parallelogram = (base × height) sq. units
base = 7 units
height = 5 units
= 7 × 5 = 35 sq. units
![]()
Question 4.
Draw as many parallelograms as possible in a grid sheet with the area 20 square units each.
Solution:

Area of parallelogram (a), (b) or (c) = 20 sq. units
Exercise 2.2
Rhombus
(Try These Textbook Page No. 41)
Question 1.
Observe the figure and answer the following questions.
(i) Name two pairs of opposite sides.
(ii) Name two pairs of adjacent sides.
(iii) Name the two diagonals.
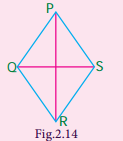
Solution:
(i) (a) PQ and RS (b) QR and PS
(ii) (a) PQ and QR (b) PS and RS
(iii) (a) PR and Question are diagonals.
Question 2.
Find the area of the rhombus given in (i) and (ii).
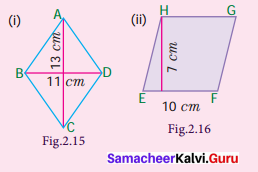
Solution:
(i) Area of the rhombus = \(\frac{1}{2}\) (d1 + d2) sq. units = \(\frac{1}{2}\)(11 + 13) sq. units
= \(\frac{1}{2}\) × (24) cm2 = 12 cm2
(ii) Base = 10 cm ; Height = 7 cm
Area of the rhombus = b × h sq. units = 10 × 7 cm2 = 70 cm2
Question 3.
Can you find the perimeter of the rhombus?
Solution:
If we know the length of one side we can find the perimeter using 4 × side units.
Question 4.
Can diagonals of a rhombus be of the same length?
Solution:
When the diagonals of a rhombus become equal it become a square.
Question 5.
A square is a rhombus but a rhombus is not a square. Why?
Solution:
In a square
(i) all sides are equal.
(ii) opposite sides are parallel
(iii) diagonals divides the square into 4 right angled triangles of equal area
(iv) the diagonals bisect each other at right angles.
So it become a rhombus also.
But in a rhombus (i) each angle need not equal to 90°.
(ii) the length of the diagonals need not be equal. Therefore it does not become a square.
Question 6.
Can you draw a rhombus in such a way that the side is equal to the diagonal.
Solution:
Yes, we can draw a rhombus with one of its diagonals equal to its side length. In such case the diagonal will divide the rhombus into two congruent equilateral triangles.
Exercise 2.3
(Try These Textbook Page No. 46)
Question 1.
Can you find the perimeter of the trapezium? Discuss.
Solution:
If all sides are given, then by adding all the four lengths we can find the perimeter of a trapezium.
Question 2.
In which case a trapezium can be divided into two equal triangles?
Solution:
If two parallel sides are equal in length. Then it can be divided into two equal triangles.
![]()
Question 3.
Mention any three life situations where the isosceles trapeziums are used?
Solution:
(i) Glass of a car windows.
(ii) Eye glass (glass in spectacles)
(iii) Some bridge supports.
(iv) Sides of handbags.