Samacheer Kalvi 10th Maths Solutions Chapter 1 Relations and Functions Unit Exercise 1

You can Download Samacheer Kalvi 10th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 1 Relations and Functions Unit Exercise 1

Question 1.
If the ordered pairs (x² – 3x, y² + 4y) and (-2, 5) are equal, then find x and y.
Solution:
(x² – 3x, y² + 4y) = (-2, 5)
x² – 3x = -2
x² – 3x + 2 = 0

Question 2.
The cartesian product A × A has 9 elements among which (-1, 0) and (0,1) are found.
Find the set A and the remaining elements of A × A.
Answer:
n(A × A) = 9
n(A) = 3
A = {-1,0,1}
A × A = {-1, 0, 1} × {-1, 0, 1}
A × A = {(-1,-1)(-1, 0) (-1, 1)
(0, -1) (0, 0) (0, 1)
(1,-1) (1, 0) (1, 1)}
The remaining elements of A × A =
{(-1, -1) (-1, 1) (0, -1) (0, 0) (1,-1) (1,0) (1,1)}

Question 3.
Given that

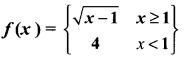
(i) f(0)
(ii) f(3)
(iii) f(a + 1) in terms of a.(Given that a > 0)
Solution:
(i) f(0) = 4
(ii) f(3) = \(\sqrt{3-1}=\sqrt{2}\)
(iii) f(a + 1) = \(\sqrt{a+1-1}=\sqrt{a}\)

Question 4.
Let A = {9,10,11,12,13,14,15,16,17} and let f : A → N be defined by f(n) = the highest prime factor of n ∈ A. Write f as a set of ordered pairs and find the range of f.
Answer:
A= {9, 10, 11, 12, 13, 14, 15, 16, 17}
f: A → N
f(x) = the highest prime factor n ∈ A
f = {(9, 3) (10, 5) (11, 11) (12, 3) (13, 13) (14, 7) (15, 5) (16, 2) (17, 17)}
Range of f = {3, 5, 11, 13, 7, 2, 17}
= {2, 3, 5, 7, 11, 13, 17}

Question 5.
Find the domain of the function f(x) = \(\sqrt{1+\sqrt{1-\sqrt{1-x^{2}}}}\)
Solution:
f(x) = \(\sqrt{1+\sqrt{1-\sqrt{1-x^{2}}}}\)
Domain of f(x) = {-1, 0, 1}
(x² = 1, -1, 0, because \(\sqrt{1-x^{2}}\) should be +ve, or 0)

Question 6.
If f (x) = x², g(x) = 3x and h(x) = x – 2, Prove that (f o g)o h = f o(g o h).
Answer:
f(x) = x² ; g(x) = 3x and h(x) = x – 2
L.H.S. = (fog) oh
fog = f[g(x)]
= f(3x)
= (3x)² = 9x²
(fog) oh = fog[h(x)]
= fog (x – 2)
= 9(x – 2)²
= 9[x² – 4x + 4]
= 9x² – 36x + 36 ….(1)
R.H.S. = fo(goh)
goh = g [h(x)]
= g(x – 2)
= 3(x – 2)
= 3x – 6
fo(goh) = fo [goh (x)]
= f(3x – 6)
= (3x – 6)²
= 9x² – 36x + 36 ….(2)
From (1) and (2) we get
L.H.S. = R.H.S.
(fog) oh = fo {goh)

Question 7.
A = {1, 2} and B = {1, 2, 3, 4} , C = {5, 6} and D = {5, 6, 7, 8} . Verify whether A × C is a subset of B × D?
Solution:
A = {1, 2), B = (1, 2, 3, 4)
C = {5, 6}, D = {5, 6, 7, 8)
A × C = {(1, 5), (1, 6), (2, 5), (2, 6)}
B × D = {(1, 5), (1, 6), (1, 7), (1, 8), (2, 5), (2, 6), (2, 7), (2, 8), (3, 5), (3, 6), (3, 7), (3, 8), (4, 5), (4, 6), (4, 7), (4, 8)}
(A × C) ⊂ (B × D) It is proved.

Question 8.
If f(x) = \(\frac{x-1}{x+1}\), x ≠ 1 show that f(f(x)) = \(-\frac{1}{x}\), Provided x ≠ 0.
Solution:

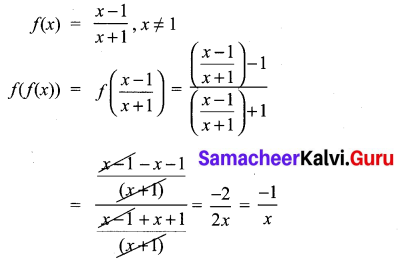
Hence it is proved.

Question 9.
The function/and g are defined by f(x) = 6x + 8; g(x) = \(\frac{x-2}{3}\).
(i) Calculate the value of \(gg\left(\frac{1}{2}\right)\)
(ii) Write an expression for g f(x) in its simplest form.
Solution:

Question 10.
Write the domain of the following real functions

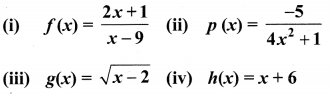
Solution:
(i) f(x) = \(\frac{2x+1}{x-9}\)
The denominator should not be zero as the function is a real function.
∴ The domain = R – {9}
(ii) p(x) = \(\frac{-5}{4 x^{2}+1}\)
The domain is R.
(iii) g(x) = \(\sqrt{x-2}\)
The domain = [2, ∝)
(iv) h(x) = x + 6
The domain is R.