Students can Download Tamil Nadu 12th Physics Model Question Paper 3 English Medium Pdf, Tamil Nadu 12th Physics Model Question Papers helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.
TN State Board 12th Physics Model Question Paper 3 English Medium
Instructions:
- The question paper comprises of four parts
- You are to attempt all the parts. An internal choice of questions is provided wherever: applicable
- All questions of Part I, II, III and IV are to be attempted separately
- Question numbers 1 to 15 in Part I are Multiple choice Questions of one mark each. These are to be answered by choosing the most suitable answer from the given four alternatives and writing the option code and the corresponding answer
- Question numbers 16 to 24 in Part II are two-mark questions. These are lo be answered in about one or two sentences.
- Question numbers 25 to 33 in Part III are three-mark questions. These are lo be answered in about three to five short sentences.
- Question numbers 34 to 38 in Part IV are five-mark questions. These are lo be answered in detail. Draw diagrams wherever necessary.
Time: 3 Hours
Max Marks: 70
PART -1
Answer all the questions. Choose the correct answer. [15 × 1 = 15]
Question 1.
Two metallic spheres of radii 1 cm and 3 cm are given charges of -1 × 10-2 C and 5 × 10-2 C respectively. If these are connected by a conducting wire, the final charge on the bigger sphere is
(a) 3 × 10-2 C
(b) 4 × 10-2 C
(c) 1 × 10-2 C
(d) 2 × 10-2 C
Answer:
(a) 3 × 10-2 C
Question 2.
What is the value of resistance of the following resistor?

(a) 100 k Ω
(b) 10 kΩ
(c) 1 k Ω
(d) 1000 k Ω
Answer:
(a) 100 k Ω
![]()
Question 3.
A flow of 107 electrons per second in a conduction wire constitutes a
(a) 1.6 × 10-26A
(b) 1.6 × 1012A
(c) 1.6 × 10-12A
(d) 1.6 × 1026A
Hint:
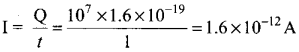
Answer:
(c) 1.6 x 10-12A
Question 4.
The force experienced by a particle having mass m and charge q accelerated through a potential difference V when it is kept under perpendicular magnetic field B is ……………….. .
(a) \(\sqrt{\frac{2 q^{3} \mathrm{BV}}{m}}\)
(b) \(\sqrt{\frac{q^{3} \mathrm{B}^{2} V}{2 m}}\)
(c) \(\sqrt{\frac{2 q^{3} \mathbf{B}^{2} \mathbf{V}}{m}}\)
(d) \(\sqrt{\frac{2 q^{3} B V}{m^{3}}}\)
Answer:
(c) \(\sqrt{\frac{2 q^{3} \mathbf{B}^{2} \mathbf{V}}{m}}\)
Question 5.
A magnetic needle is kept in a non-uniform magnetic field. It experiences
(a) a force and a torque
(b) a force but not a torque
(c) a torque but not a force
(d) neither a force nor a torque
Answer:
(a) a force and a torque
Question 6.
The instantaneous values of alternating current and voltage in a circuit are i = \(\frac{1}{\sqrt{2}}\) sin( 100πt) A and v = \(\frac{1}{\sqrt{2}} \sin \left(100 \pi t+\frac{\pi}{3}\right) \mathrm{V}\) The average power in watts consumed in the circuit is
(a) \(\frac{1}{4}\)
(b) \(\frac{\sqrt{3}}{4}\)
(c) \(\frac{1}{2}\)
(d) \(\frac{1}{8}\)
Answer:
(d) \(\frac{1}{8}\)
Question 7.
Which of the following is an electromagnetic wave’?
(a) α – rays
(b) β – rays
(c) γ – rays
(d) all of them
Answer:
(c) γ – rays
Question 8.
When light is incident on a soap film of thickness 5 × 10-5 cm, the wavelength of light reflected maximum in the visible region is 5320 Å. Refractive index of the film will be.
(a) 1.22
(b) 1.33
(c) 1.51
(d) 1.83
Hint. The condition for constructive interference, (for reflection)

Answer:
(b) 1.33
Question 9.
A plane glass is placed over a various coloured letters (violet, green, yellow, red) The letter which appears to be raised more is,
(a) red
(b) yellow
(c) green
(d) violet
Hint. Letters appear to be raised depending upon the refractive index of the material. Since violet has a higher refractive index than red (the index increases with frequency), red will be the lowermost.
Answer:
(d) violet
![]()
Question 10.
In photoelectric emission, a radiation whose frequency is 4 times threshold frequency of a certain metal is incident on the metal. Then the maximum possible velocity of the emitted electron will be
(a) \(\sqrt{\frac{h v_{0}}{m}}\)
(b) \(\sqrt{\frac{6 h u_{0}}{m}}\)
(c) \(2 \sqrt{\frac{h v_{0}}{m}}\)
(d) \(\sqrt{\frac{h v_{0}}{2 m}}\)
Hint: From Einstein’s photoelectric equation
Kmax = hυ – hυ0 [υ = 4υ0]
\(\frac { 1 }{ 2 }\) mV2max = 4hυ0 – hυ0
V2max = \(\frac{6 h v_{0}}{m}\)
Vmax = \(\sqrt{\frac{6 h v_{0}}{m}}\)
Answer:
(b) \(\sqrt{\frac{6 h u_{0}}{m}}\)
Question 11.
The number of photo-electrons emitted for light of a frequency u (higher than the threshold frequency υ0) is proportional to
(a) Threshold frequency (υ0)
(b) Intensity of light
(c) Frequency of light (υ)
(d) υ – υ0
Hint: Photoelectric current of Intensity of incident light
Answer:
(b) Intensity of light
Question 12.
Atomic number of H-like atom with ionization potential 122.4 V for n = 1 is
(a) 1
(b) 2
(c) 3
(d) 4
Hint: The ionisation energy of a hydrogen atom is, IE = \(\frac{13.6 z^{2}}{n^{2}}\)
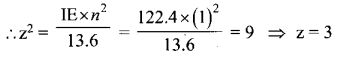
Answer:
(c) 3
Question 13.
The given electrical network is equivalent to ………….. .
(а) AND gate
(b) OR gate
(c) NOR gate
(d) NOT gate
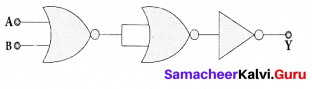
Answer:
(c) NOR gate
Question 14.
The frequency range of 3 MHz to 30 MHz is used for
(a) Ground wave propagation
(b) Space wave propagation
(c) Sky wave propagation
(d) Satellite communication
Answer:
(c) Sky wave propagation
Question 15.
Which one of the following is the natural nanomaterial?
(a) Peacock feather
(b) peacock beak
(c) Grain of sand
(d) Skin of the wale
Answer:
(a) Peacock feather
PART – II
Answer any six questions in which Q. No 21 is compulsory. [6 × 2 = 12]
Question 16.
When two objects are rubbed with each other, approximately a charge of 50 nC can be produced in each object. Calculate the number of electrons that must be transferred to produce this charge.
Answer:
Charge produced in each object q = 50 nC
q = 50 × 10-9C
Charge of electron (e) = 1.6 × 10-19C
Number of electron transferred, n = \(\frac{q}{e}=\frac{50 \times 10^{-9}}{1.6 \times 10^{-19}}\) = ,n =31.25 × 10-9 × 1019
n = 31.25 × 1o10 electrons
Question 17.
State Kirchhoff’s voltage rule.
Answer:
It states that in a closed circuit the algebraic sum of the products of the current and resistance of each part of the circuit is equal to the total emf included in the circuit. This rule follows from the law of conservation of energy for an isolated system.
![]()
Question 18.
Define magnetic dipole moment.
Answer:
The magnetic dipole moment is defined as the product of its pole strength and magnetic length.
\(\overrightarrow{\mathrm{P}}\) = qm\(\overrightarrow{\mathrm{d}}\)
Question 19.
What is meant by ‘Wattful current’?
Answer:
The component of current (IRMS cos Φ) which is in phase with the voltage is called active component. The power consumed by this current = VRMSIRMS cos Φ . So that it is also known as ‘WattfuT current.
Question 20.
What are electromagnetic waves?
Answer:
Electromagnetic waves are non-mechanical waves which move with speed equals to the speed of light (in vacuum).
Question 21.
Two light sources have intensity of light as 10. What is the resultant intensity at a point where the two light waves have a phase difference of π/3?
Answer:
Let the intensities be I0.
The resultant intensity is, I = 4 I0 cos2 (φ/2)
Resultant intensity when, Φ = π / 3, is I = 4I0 cos2 (π / 6)
I = 4I0(√3/2)2 = 3I0
Question 22.
State de Broglie hypothesis.
Answer:
De Broglie hypothesis, all matter particles like electrons, protons, neutrons in motion are associated with waves.
Question 23.
Calculate the energy equivalent of 1 atomic mass unit.
Answer:
We take, m = 1 amu = 1.66 × 1027 kg
c = 3 × 108 ms-1
Then, E = mc2 = 1.66 × 1027 × (3 × 1o8)27 J
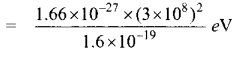
E ≈ 981 MeV
∴ 1 amu = 931 MeV
Question 24.
hat do you mean by doping?
Answer:
The process of adding impurities to the intrinsic semiconductor is called doping.
![]()
PART III
Answer any six questions in which Q.No. 32 is compulsory. [6 × 3 = 18]
Question 25.
What are the differences between Coulomb force and gravitational force?
Answer:
- The gravitational force between two masses is always attractive but Coulomb force between two charges can be attractive or repulsive, depending on the nature of charges.
- The value of the gravitational constant G = 6.626 × 1011 N m2 kg-2. The value of the constant k in Coulomb law is k = 9 × 109 N m2 C-2.
- The gravitational force between two masses is independent of the medium. The electrostatic force between the two charges depends on nature of the medium in which the two charges are kept at rest.
- The gravitational force between two point masses is the same whether two masses are at rest or in motion. If the charges are in motion, yet another force (Lorentz force) comes into play in addition to coulomb force.
Question 26.
The resistance of a nichrome wire at 0 °C is 10 Ω. If its temperature coefficient of resistance is 0.004/°C, find its resistance at boiling point of water. Comment on the result.
Answer:
Resistance of a nichrome wire at 0°C, R0 = 10 Ω
Temperature co-efficient of resistance, α = 0.004/°C
Resistance at boiling point of water, RT = ?
Temperature of boiling point of water, T = 100 °C
RT = R0 ( 1 + α T) = 10[1 + (0.004 × 100)]
RT = 10(1 + 0.4) = 10 × 1.4
RT = 14Ω
As the temperature increases the resistance of the wire also increases.
Question 27.
What is meant by magnetic induction?
Answer:
The magnetic induction (total magnetic held) inside the specimen \(\overrightarrow{\mathrm{B}}\) is equal to the sum of the magnetic field \(\overrightarrow{\mathrm{B}}\)0 produced in vacuum due to the magnetising field and the magnetic field \(\overrightarrow{\mathrm{B}}\)m due to the induced magnetisation of the substance.
![]()
Question 28.
An inductor blocks AC but it allows DC. Why? and How?
Answer:
An inductor L is a closely wound helical coil. The steady DC current flowing through L produces uniform magnetic field around it and the magnetic flux linked remains constant. Therefore there is no self-induction and self-induced emf (back emf). Since inductor behaves like a resistor, DC flows through an inductor.
The AC flowing through L produces time-varying magnetic field which in turn induces self- induced emf (back emf)- This back emf, according to Lenz’s law, opposes any change in the current. Since AC varies both in magnitude and direction, its flow is opposed in L. For an ideal inductor of zero ohmic resistance, the back emf is equal and opposite to the applied emf. Therefore L blocks AC.
Question 29.
Derive the relation between/and R for a spherical mirror.
Answer:
Let C be the centre of curvature of the mirror. Consider a light ray parallel to the principal axis is incident on the mirror at M and passes through the principal focus F after reflection. The geometry of reflection of the incident ray is shown in figure. The line CM is the normal to the mirror at M. Let i be the angle of incidence and the same will be the angle of reflection.
If MP is the perpendicular from M on the principal axis, then from the geometry, The angles
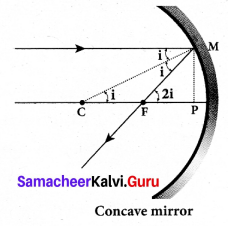
∠MCP = i and ∠MFP = 2i From right angle triangles ∆MCP and ∆MFP,
tan i = \(\frac{P M}{P C}\) and tan 2i = \(\frac{P M}{P F}\)
As the angles are small, tan i ≈ i, i = \(\frac{P M}{P C}\) and 2i = \(\frac{P M}{P F}\)
Simplifying further, 2 \(\frac{\mathrm{PM}}{\mathrm{PC}}=\frac{\mathrm{PM}}{\mathrm{PF}}\) ; 2PF = PC
PF is focal length f and PC is the radius of curvature R.
2f = R (or) f = \(\frac{R}{2}\)
f = \(\frac{R}{2}\) is the relation between/and R.
![]()
Question 30.
What is a photo cell? Mention the different types of photocells.
Answer:
photocells: Photo electric cell or photo cell is a device which converts light energy into electrical energy. It works on the principle of photo electric effect.
Types:
- Photo emissive cell
- Photo voltaic cell
- Photo conductive cell
Question 31.
Show that nuclear density is almost constant for nuclei with Z > 10.
Answer:
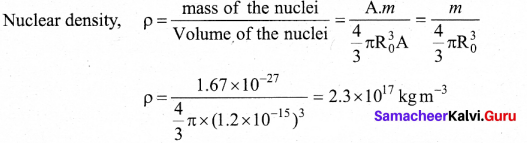
The expression shows that the nuclear density is independent of the mass number A. In other words, all the nuclei (Z >10) have the same density and it is an important characteristics of the nuclei.
Question 32.
Calculate the range of the variable capacitor that is to be used in a tuned-collector oscillator which has a fixed inductance of 150 pH. The frequency band is from 500 kHz to 1500 kHz.
Answer:
Resonant frequency f0 = \(\frac{1}{2 \pi \sqrt{\mathrm{LC}}}\)
On simplifying we get C = \(\frac{1}{4 \pi^{2} f_{0}^{2} L}\)
When frequency is equal to 500 kHz
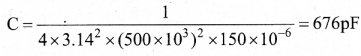
When frequency is equal to 1500 kHz
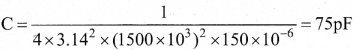
There fore, the capacitor range is 75 – 676 pF
Question 33.
Distinguish between wireline and wireless communication.
Answer:
|
Wireline communication |
Wireless communication |
| It is a point-to-point communication. | It is a broadcast mode communication. |
| It uses mediums like wires, cable and optical fibres. | It uses free space as a communication medium. |
| These systems cannot be used for long distance transmission as they are connected. | These systems can be used for long distance transmission. |
| Ex. telephone, intercom and cable TV. | Ex. mobile, radio or TV broadcasting and satellite communication. |
![]()
PART – IV
Answer all the questions. [5 × 5 = 25]
Question 34.
(a) Explain in detail the construction and working of a Van de Graaff generator.
Answer:
Principle: Electrostatic induction and action at points.
Construction: A large hollow spherical conductor is fixed on the insulating stand. A pulley B is mounted at the center of the hollow sphere and another pulley C is fixed at the bottom. A belt made up of insulating materials like silk or rubber runs over both pulleys. The pulley C is driven continuously by the electric motor. Two comb shaped metallic conductors E and D are ‘ fixed near the pulleys.
The comb D is maintained at a positive potential of 104 V by a power supply. The upper comb E is connected to the inner side of the hollow metal sphere.
Working: Due to the high electric field near comb D, air between the belt and comb D gets ionized. The positive charges are pushed towards the belt and negative charges are attracted towards the comb D. The positive charges stick to the belt and move up. When the positive charges reach the comb E, a large amount of negative and positive charges are induced on either side of comb E due to electrostatic induction. As a result, the positive charges are pushed away from the comb E and they reach the outer surface of the sphere. Since the sphere is a conductor, the positive charges are distributed uniformly on the outer surface of the hollow sphere. At the same time, the negative charges nullify the positive charges in the belt due to corona discharge before it passes over the pulley.
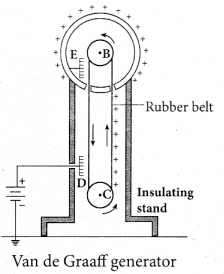
When the belt descends, it has almost no net charge. At the bottom, it again gains a large positive charge. The belt goes up and delivers the positive charges to the outer surface of the sphere. This process continues until the outer surface produces the potential difference of the order of 107 V which is the limiting value. We cannot store charges beyond this limit since the extra charge starts leaking to the surroundings due to ionization of air. The leakage of charges can be reduced by enclosing the machine in a gas filled steel chamber at very high pressure. Uses: The high voltage produced in this Van de Graaff generator is used to accelerate positive ions (protons and deuterons) for nuclear disintegrations and other applications.
[OR]
Question 34.
(b) Explain the equivalent resistance of a series resistor network.
Answer:
Resistors in series: When two or more resistors are connected end to end, they are said to be in series. The resistors could be simple resistors or bulbs or heating elements or other devices. Fig. (a) shows three resistors R1, R2 and R3 connected in series.
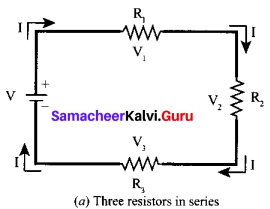
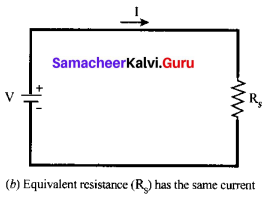
The amount of charge passing through resistor R1 must also pass through resistors R2 and R3 since the charges cannot accumulate anywhere in the circuit. Due to this reason, the current I passing through all the three resistors is the same. According to Ohm’s law, if same current pass through different resistors of different values, then the potential difference across each resistor must be different. Let V1, V2 and V3 be the potential difference (voltage) across each of the resistors R1, R2 and R3 respectively, then we can write V1 = IR1 V2 = IR2 and V3 = IR3. But the total voltage V is equal to the sum of voltages across each resistor.
V = V1 + V2 + V3
= IR1 + IR2 + IR3 ….. (1)
V = I(R1 + R2 + R3)
V = I.Rs ….. (2)
where Rs is the equivalent resistance,
Rs = R1 + R2 + R3 ….. (3)
When several resistances are connected in series, the total or equivalent resistance is the sum of the individual resistances as shown in fig. (b).
Note: The value of equivalent resistance in series connection will be greater than each individual resistance.
![]()
Question 35.
(a) Deduce the relation for the magnetic induction at a point due to an infinitely long straight conductor carrying current.
Answer:
Magnetic field due to long straight conductor carrying current: Consider a long straight wire NM with current I flowing from N to M. Let P be the point at a distance a from point O. Consider an element of length dl of the wire at a distance l from point O and \(\vec{r}\) be the vector joining the element dl with the point P. Let θ be the angle between dl and \(\vec{r}\) Then, the magnetic field at P due to the element is
\(d \overrightarrow{\mathrm{B}}=\frac{\mu_{0} \mathrm{Id} \vec{l}}{4 \pi r^{2}} \sin \theta\) (unit vector perpendicular to \(d \vec{l}\) and \(\vec{r}\) )-(1)
The direction of the field is perpendicular to the plane of the paper and going into it. This can be determined by taking the cross product between two vectors \(d \vec{l}\) and \(\vec{r}\) (let it be n̂). The net magnetic field can be determined by integrating equation with proper limits.
\(\vec{B}\) = ∫d\(\vec{B}\)
From the figure, in a right angle triangle PAO,
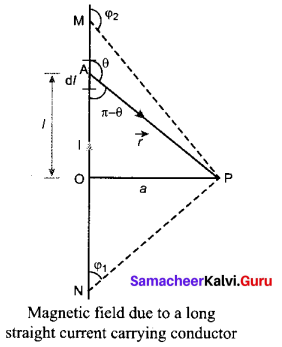
tan (π – θ) = \(\frac{a}{l}\)
l = \(-\frac{a}{\tan \theta}\) (since tan (π – θ) = – tan θ) ⇒ \(\frac{1}{\tan \theta}\) = cot θ
l = -a cot θ and r = a cosecθ
Differentiating,
dl = a cosec2θ dθ

This is the magnetic field at a point P due to the current in small elemental length. Note that we have expressed the magnetic field OP in terms of angular coordinate i.e. θ. Therefore, the net magnetic field at the point P which can be obtained by integrating \(d \vec{B}\) by varying the angle from θ = φ1 to θ = φ2 is

For a an infinitely long straight wire, l = 0 and 2 = , the magnetic field is
\(\overrightarrow{\mathrm{B}}=\frac{\mu_{0} I}{2 \pi a} \hat{n}\) …… (3)
Note that here n̂ represents the unit vector from the point O to P.
[OR]
Question 35.
(b) Show that the mutual inductance between a pair of coils is same (M12 = M21).
Answer:
Mutual induction: When an electric current passing through a coil changes with time, an emf is induced in the neighbouring coil. This phenomenon is known as mutual induction and the emf is called mutually induced emf.
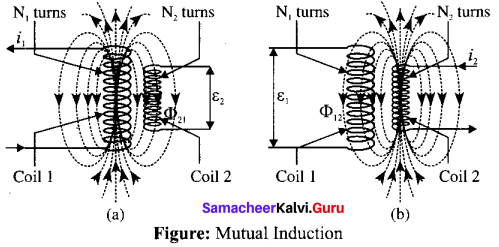
Consider two coils which are placed close to each other. If an electric current q is sent through coil i1 the magnetic field produced by it is also linked with coil 2.
Let Φ21 be the magnetic flux linked with each turn of the coil 2 of N2 turns due to coil 1, then the total flux linked with coil 2 (N2Φ21) is proportional to the current i1 in the coil 1.
N2Φ21 ∝ i1
N2Φ21 = M21i1 or M21 = \(\frac{N_{2} \Phi_{21}}{i_{1}}\)
The constant of proportionality M21 is the mutual inductance of the coil 2 with respect to coil 1. It is also called as coefficient of mutual induction. If i1 = 1 A, then M21 = N2Φ21.
Therefore, the mutual inductance M21 is defined as the flux linkage of the coil 2 when 1A current flows through coil 1.
When the current i1 changes with time, an emf ξ2 is induced in coil 2. From Faraday’s law of electromagnetic induction, this mutually induced emf ξ21 is given by
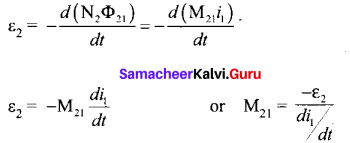
The negative sign in the above equation shows that the mutually induced emf always opposes the change in current with respect to time. If \(\frac{d i_{1}}{d t}\) = 1 As-1, then M21 = -ξ2.
Mutual inductance M21 is also defined as the opposing emf induced in the coil 2 when the rate of change of current through the coil I is l As-1.
Similarly, if an electric current i2 through coil 2 changes with time, then emf ξ1 is induced in coil 1. Therefore, N
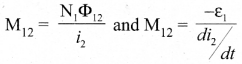
where M12 is the mutual inductance of the coil I with respect to coil 2. It can be shown that for a given pair of coils, the mutual inductance is same. i.e., M21 = M12 = M.
In general, the mutual induction between two coils depends on size, shape, the number of turns of the coils, their relative orientation and permeability of the medium.
![]()
Question 36.
(a) Derive the equation for refraction at single spherical surface. Equation for refraction at single spherical surface:
Answer:
Let us consider two transparent media having refractive indices n1 and n2 are separated by a spherical surface. Let C be the centre of curvature of the spherical surface. Let a point object O be in the medium n1. The line OC cuts the spherical surface at the pole P of the surface. As the rays considered are paraxial rays, the perpendicular dropped for the point of incidence to the principal axis is very close to the pole or passes through the pole itself.
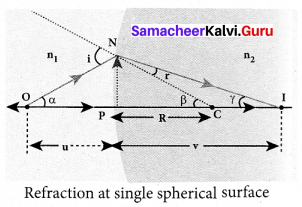
Light from O falls on the refracting surface at N. The normal drawn at the point of incidence passes through the centre of curvature C. As n2 > n1, light in the denser medium deviates towards the normal and meets the principal axis at I where the image is formed. Snell’s law in product form for the refraction at the point N could be written as,
n1 sin i = n2 sin r …… (1)
As the angles are small, sin of the angle could be approximated to the angle itself.
n1i = n2r ……… (2)
Let the angles
∠NOP = α ∠NCP = β ∠NIP = γ
tan α = \(\frac{P N}{P O}\) tan β = \(\frac{P N}{P C}\) tan γ = \(\frac{P N}{P I}\)
As these angles are small, tan of the angle could be approximated to the angle itself.
α = \(\frac{P N}{P O}\) ; β = \(\frac{P N}{P C}\) ; γ = \(\frac{P N}{P I}\) …… (3)
For the triangle, ∆ONC,
i = α + β ….. (4)
For the triangle, ∆INC,
β = r + γ (or) r = β – γ …… (5)
Substituting for i and r from equations (4) and (5) in the equation (2).
n1 (α + β) = n2 (β – γ)
Rearranging,
n1α + n2γ = (n2 – n1)β
Substituting for α, β and γ from equation (3)
\(n_{1}\left(\frac{\mathrm{PN}}{\mathrm{PO}}\right)+n_{2}\left(\frac{\mathrm{PN}}{\mathrm{PI}}\right)=\left(n_{2}-n_{1}\right)\left(\frac{\mathrm{PN}}{\mathrm{PC}}\right)\)
Further simplifying by cancelling method
\(\frac{n_{1}}{\mathrm{PO}}+\frac{n_{2}}{\mathrm{PI}}=\frac{n_{2}-n_{1}}{\mathrm{PC}}\) ….. (6)
Following sign conventions, PO = -υ , PI = +ν and PC = +R in equation (6),
\(\frac{n_{1}}{-u}+\frac{n_{2}}{v}=\frac{\left(n_{2}-n_{1}\right)}{\mathrm{R}}\)
After rearranging, finally we get,
\(\frac{n_{2}}{v}-\frac{n_{1}}{u}=\frac{\left(n_{2}-n_{1}\right)}{\mathrm{R}}\) ……… (7)
Equation (7) gives the relation among the object distance υ, image distance ν , refractive indices of the two media (nl and n2) and the radius of curvature R of the spherical surface. It holds for any spherical surface.
If the first medium is air then, n1 = 1 and the second medium is taken just as n2 = n, then the equation is reduced to,
\(\frac{n}{v}-\frac{1}{u}=\frac{(n-1)}{\mathrm{R}}\) ……… (8)
![]()
[OR]
Question 36.
(b) What do you mean by electron emission? Explain briefly various methods of electron emission.
Answer:
Electron emission:
- Free electrons possess some kinetic energy and this energy is different for different electrons. The kinetic energy of the free electrons is not sufficient to overcome the surface barrier.
- Whenever an additional energy is given to the free electrons, they will have sufficient energy to cross the surface barrier. And they escape from the metallic surface.
- The liberation of electrons from any surface of a substance is called electron emission. There are mainly four types of electron emission which are given below.
(i) Thermionic emission:
When a metal is heated to a high temperature, the free electrons on the surface of the metal get sufficient energy in the form of thermal energy so that they are emitted from the metallic surface. This type of emission is known as thermionic emission.
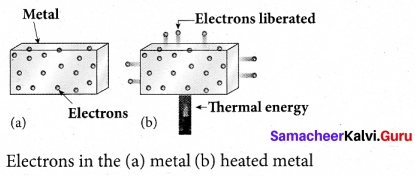
The intensity of the thermionic emission (the number of electrons emitted) depends on the metal used and its temperature.
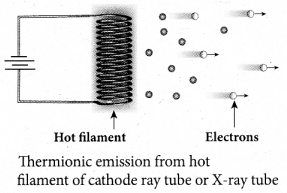
Examples: cathode ray tubes, electron microscopes, X-ray tubes etc.
(ii) Field emission:
Electric field emission occurs when a very strong electric field is applied across the metal. This strong field pulls the free electrons and helps them to overcome the surface barrier of the metal.
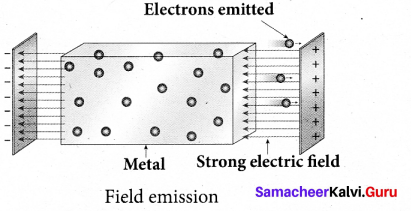
Field emission
Examples: Field emission scanning electron microscopes, Field-emission display etc.
(iii) Photo electric emission:
When an electromagnetic radiation of suitable frequency is incident on the surface of the metal, the energy is transferred from the radiation to the.free electrons. Hence, the free electrons get sufficient energy to cross the surface barrier and the photo electric emission takes place. The number of electrons emitted depends on the intensity of the incident radiation.
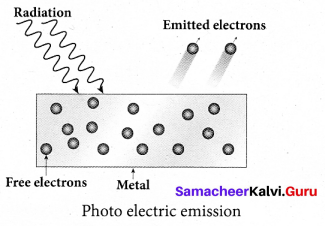
Examples: Photo diodes, photo electric cells etc.
(iv) Secondary emission:
When a beam of fast moving electrons strikes the surface of the metal, the kinetic energy of the striking electrons is transferred to the free electrons on the metal surface. Thus the free electrons get sufficient kinetic energy so that the secondary emission of electron occurs.
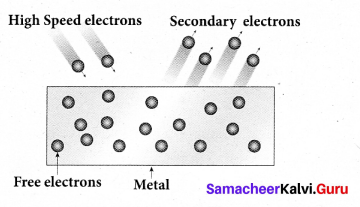
Examples: Image intensifires, photo multiplier tubes etc.
Question 37.
(a) Discuss the spectral series of hydrogen atom.
Answer:
The spectral lines of hydrogen are grouped in separate series. In each series, the distance of separation between the consecutive wavelengths decreases from higher wavelength to the lower wavelength, and also wavelength in each series approach a limiting value known as the series limit. These series are named as Lyman series. Balmer series, Paschen series, Brackett series, Pfund series, etc. The wavelengths of these spectral lines perfectly agree with the equation derived from Bohr atom model.
\(\frac{1}{\lambda}=\mathrm{R}\left(\frac{1}{n^{2}}-\frac{1}{m^{2}}\right)=\bar{v}\) …… (1)
where ν̂ is known as wave number which is inverse of wavelength, R is known as Rydberg constant whose value is 1.09737 × 107 m-1 and m and n are positive integers such that m > n. The various spectral series are discussed below:
(a) Lyman series:
Put n = 1 and m = 2,3,4 in equation (I). The wave number or wavelength of spectral lines of Lyman series which lies in ultra-violet region is
\(\bar{v}=\frac{1}{\lambda}=\mathrm{R}\left(\frac{1}{1^{2}}-\frac{1}{m^{2}}\right)\)
(b) Balmer series:
Put n = 2 and m = 3,4,5 in equation (I). The wave number or wavelength of spectral lines of Balmer series which lies in visible region is
\(\bar{v}=\frac{1}{\lambda}=\mathrm{R}\left(\frac{1}{2^{2}}-\frac{1}{m^{2}}\right)\)
(c) Paschen series:
Put n = 3 and m = 4,5,6 in equation (I). The wave number or wavelength of spectral lines of Paschen series which lies in infra-red region (near IR) is
\(\bar{v}=\frac{1}{\lambda}=\mathrm{R}\left(\frac{1}{3^{2}}-\frac{1}{m^{2}}\right)\)
(d) Brackett series:
Put n = 4 and m = 5,6,7 in equation (I). The wave number or wavelength of spectral lines of Brackett series which lies in infra-red region (middle IR) is
\(\bar{v}=\frac{1}{\lambda}=\mathrm{R}\left(\frac{1}{4^{2}}-\frac{1}{m^{2}}\right)\)
(e) Pfund series:
Put n = 5 and m = 6,7,8 in equation (I). The wave number or wavelength of spectral lines of Pfund series which lies in infra-red region (far IR) is
\(\bar{v}=\frac{1}{\lambda}=\mathrm{R}\left(\frac{1}{5^{2}}-\frac{1}{m^{2}}\right)\)
![]()
[OR]
Question 37.
(b) State and prove De Morgan’s First and Second theorems.
Answer:
De Morgan’s First Theorem:
The first theorem states that the complement of the sum of two logical inputs is equal to the product of its complements.
Proof:
The Boolean equation for NOR gate is Y = \(\overline{\mathrm{A}+\mathrm{B}}\) . The Boolean equation for a bubbled AND gate is Y = \(\overline{\mathrm{A}} \cdot \overline{\mathrm{B}}\) Both cases generate same outputs for same inputs. It can be verified using the following truth table.
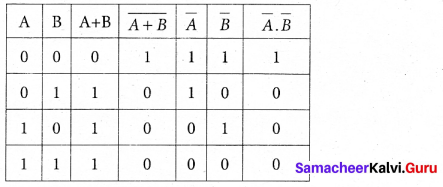
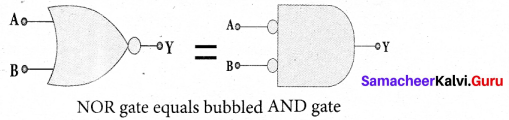
From the above truth table, we can conclude \(\overline{\mathrm{A}+\mathrm{B}}=\overline{\mathrm{A}} \cdot \overline{\mathrm{B}}\). Thus De Morgan’s First Theorem is proved. It also says that a NOR gate is equal to a bubbled AND gate. The corresponding logic circuit diagram is shown in figure.
De Morgan’s Second Theorem:
The second theorem states that the complement of the product of two inputs is equal to the sum of its complements.
Proof
The Boolean equation for NAND gate is Y = \(\overline{\mathrm{AB}}\)
The Boolean equation for bubbled OR gate is Y = \(\overline{\mathrm{A}}+\overline{\mathrm{B}}\) . A and B are the inputs and Y is the output. The above two equations produces the same output for the same inputs. It can be verified by using the truth table.

From the above truth table we can conclude \(\overline{\mathrm{A} . \mathrm{B}}=\overline{\mathrm{A}}+\overline{\mathrm{B}}\). Thus De Morgan’s Second Theorem is proved. It also says, a NAND gate is equal to a bubbled OR gate. The corresponding logic circuit diagram is shown in figure.
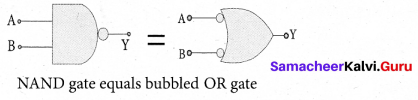
![]()
Question 38.
(a) What is modulation? Explain the types of modulation with necessary diagrams.
Answer:
Modulation: For long distance transmission, the low frequency baseband signal (input signal) is superimposed onto a high frequency radio signal by a process called modulation.
There are 3 types of modulation based on which parameter is modified. They are
(i) Amplitude modulation,
(ii) Frequency modulation, and
(iii) Phase modulation.
(i) Amplitude Modulation (AM):
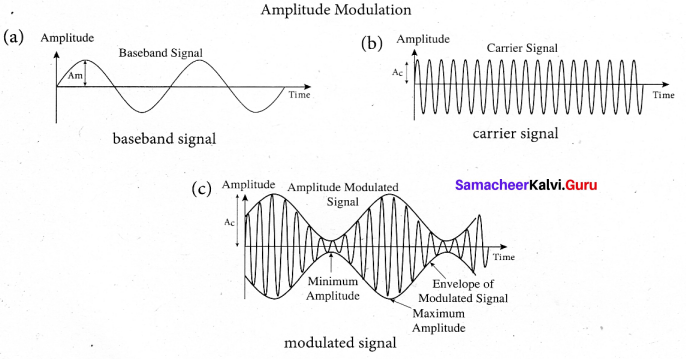
If the amplitude of the carrier signal is modified according to the instantaneous amplitude of the baseband signal, then it is called amplitude modulation. Here the frequency and the phase of the carrier signal remain constant. Amplitude modulation is used in radio and TV broadcasting.
The signal shown in figure (a) is the message signal or baseband signal that carries information, figure (b) shows the high frequency carrier signal and figure (c) gives the amplitude modulated signal. We can see clearly that the carrier wave is modified in proportion to the amplitude of the baseband signal.
Amplitude Modulation
(ii) Frequency Modulation (FM):
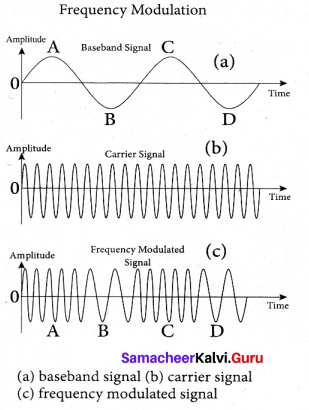
The frequency of the camer signal is modified according to the instantaneous amplitude of the baseband signal in frequency modulation. Here the amplitude and the phase of the carrier signal remain constant. Increase in the amplitude of the baseband signal increases the frequency of the carrier signal and vice versa. This leads to compressions and rarefactions in the frequency spectrum of the modulated wave. Louder signal leads to compressions and relatively weaker signals to rarefactions. When the amplitude of the baseband signal is zero in Figure (a), the frequency of the modulated signal is the same as the carrier signal. The frequency of the modulated wave increases when the amplitude of the baseband signal increases in the positive direction
(A, C). The increase in amplitude in the negative half cycle (B,D) reduces the frequency of the modulated wave (figure (c)).
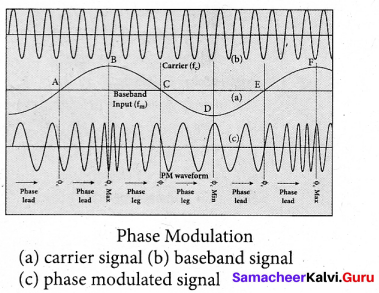
(iii) Phase Modulation (PM):
The instantaneous amplitude of the baseband signal modifies the phase of the camer signal keeping the amplitude and frequency constant is called phase modulation. This modulation is used to generate frequency modulated signals. It is similar to frequency modulation except that the phase of the carrier is varied instead of varying frequency. The carrier phase changes according to increase or decrease in the amplitude of the baseband signal. When the modulating signal goes positive, the amount of phase
lead increases with the amplitude of the modulating signal. Due to this, the carrier signal is compressed or its frequency is increased.
On the other hand, the negative half cycle of the baseband signal produces a phase lag in the carrier signal. This appears to have stretched the frequency of the carrier wave. Hence similar to frequency modulated wave, phase modulated wave also comprises of
compressions and rarefactions. When the signal voltage is zero (A, C and E) the carrier frequency is unchanged.
[OR]
![]()
Question 38.
(b) Elaborate any two types of Robots with relevant examples.
Answer:
(i) Human Robot:
Certain robots are made to resemble humans in appearance and replicate the human activities like walking, lifting, and sensing, etc.
- Power conversion unit: Robots are powered by batteries, solar power, and hydraulics.
- Actuators: Converts energy into movement. The majority of the actuators produce rotational or linear motion.
- Electric motors: They are used to actuate the parts of the robots like wheels, arms, fingers, legs, sensors, camera, weapon systems etc. Different types of electric motors are used. The most often used ones are AC motor, Brushed DC motor, Brushless DC motor, Geared DC motor, etc.
- Pneumatic Air Muscles: They are devices that can contract and expand when air is pumped inside. It can replicate the function of a human muscle. They contract almost 40% when the air is sucked inside them.
- Muscle wires: They are thin strands of wire made of shape memory alloys. They can contract by 5% when electric current is passed through them.
- Piezo Motors and Ultrasonic Motors: Basically, we use it for industrial robots.
- Sensors: Generally used in task environments as it provides information of real-time knowledge.
- Robot locomotion: Provides the types of movements to a robot. The different types are (a) Legged (b) Wheeled (c) Combination of Legged and Wheeled Locomotion (d) Tracked slip/skid
(ii) Industrial Robots:
Six main types of industrial robots:
- Cartesian
- SCARA (Selective Compliance Assembly Robot Arm)
- Cylindrical
- Delta
- Polar
- Vertically articulated
Six-axis robots are ideal for:
- Arc Welding
- Spot Welding
- Material Handling
- Machine Tending
- Other Applications