Tamil Nadu 11th Maths Model Question Paper 5 English Medium

Students can Download Tamil Nadu 11th Maths Model Question Paper 5 English Medium Pdf, Tamil Nadu 11th Maths Model Question Papers helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

TN State Board 11th Maths Model Question Paper 5 English Medium

General Instructions:

1. The question paper comprises of four parts.
2. You are to attempt all the parts. An internal choice of questions is provided wherever applicable.
3. All questions of Part I, II, III and IV are to be attempted separately.
4. Question numbers 1 to 20 in Part I are Multiple Choice Questions of one mark each.
   These are to be answered by choosing the most suitable answer from the given four alternatives and writing the option code and the corresponding answer
5. Question numbers 21 to 30 in Part II are two-mark questions. These are to be answered in about one or two sentences.
6. Question numbers 31 to 40 in Part III are three-mark questions. These are to be answered in above three to five short sentences.
7. Question numbers 41 to 47 in Part IV are five-mark questions. These are to be answered in detail Draw diagrams wherever necessary.

Time: 2.30 Hours
Maximum Marks: 90

PART – I

I. Choose the correct answer. Answer all the questions. [20 × 1 = 20]

Question 1.
Let X= {1,2, 3, 4} and R = {(1, 1), (1, 2), (1, 3), (2, 2), (3, 3) (2, 1), (3, 1), (1, 4), (4, 1)} then R is……………
(a) reflexive
(b) symmetric
(c) transitive
(d) equivalence
Solution:
(b) symmetric

Question 2.
Find a so that the sum and product of the roots of the equation 2x² – (a – 3)x + 3a – 5 = 0 are equal is…………
(a) 1
(b) 2
(c) 3
(d) 4
Solution:
(b) 2

Question 3.
If π < 2θ < \(\frac{3π}{2}\) then \(\sqrt{2+\sqrt{2+2 \cos 4 \theta}}\) = ………….
(a) -2 cos θ
(b) -2 sin θ
(c) 2 cos θ
(d) 2 sin θ
Solution:
(d) 2 sin θ

Question 4.
If f(θ) = |sin θ| + |cos θ|, θ ∈ R then f(θ) is in the interval……………
(a) [0, 2]
(b) [1, √2]
(c) [ 1, 2]
(d) [0, 1]
Solution:
(b) [1, √2]

Question 5.
Total number of words formed by 2 vowels and 3 consonants taken from 4 vowels and 5 consonants is equal to…………
(a) 60
(b) 600
(c) 720
(d) 7200
Solution:
(d) 7200

Question 6.
The number of parallelograms that can be formed from a set of four parallel lines intersecting another set of three parallel lines is…………
(a) 6
(b) 9
(c) 12
(d) 18
Solution:
(d) 18

Question 7.
The nth term of the sequence \(\frac{1}{3}\), \(\frac{3}{4}\), \(\frac{7}{8}\),\(\frac{15}{16}\)…. is …………..
(a) 2ⁿ – n – 1
(b) 1 – 2^-n
(c) 2^-n + n – 1
(d) 2^n-1
Solution:
(b) 1 – 2^-n

Question 8.
The remainder when 3815 is divided by 13 is…………
(a) 12
(b) 1
(c) 11
(d) 5
Solution:
(a) 12

Question 9.
If the straight line joining the points (2, 3) and (-1, 4) passes through the point (α, β) then…………
(a) α + 2β = 7
(b) 3α + β = 9
(c) α + 3β = 11
(d) 3α + β = 11
Solution:
(c) α + 3β = 11

Question 10.
If the equation of the base opposite to the vertex (2, 3) of an equilateral triangle is x + y = 2 then the length of a side is………….
(a) \(\sqrt{\frac{3}{2}}\)
(b) 6
(c) √6
(d) 3√2
Solution:
(c) √6

Question 11.
If A and B are symmetric matrices of order n where A ≠ B then…………
(a) A + B is skew symmetric
(b) A + B is symmetric
(c) A + B is a diagonal matrix
(d) A + B is a zero matrix
Solution:
(b) A + B is symmetric

Question 12.
If A is a square matrix then which of the following is not symmetric?
(a) A + A^T
(b) AA^T
(c) A^TA
(d) A – A^T
Solution:
(d) A – A^T

Question 13.
\(\lim _{x \rightarrow \infty}\) \(\frac{a^x-b^x}{x}\) = …………….
(a) log ab
(b) log \(\frac{a}{b}\)
(c) log log \(\frac{b}{a}\)
(d) \(\frac{a}{b}\)
Solution:
(b) log \(\frac{a}{b}\)

Question 14.
The function f(x) =  is discontinuous at ………..
(a) x = 0
(b) x = 1
(c) x = -2
(d) x = 2
Solution:
(d) x = 2

Question 15.
The function f(x) = \(\left\{\begin{array}{ll} 2 & x \leq 1 \\ x & x>1 \end{array}\right.\) is not differentiable at………..
(a) x = 0
(b) x = 1
(c) x = -1
(d) x = 2
Solution:
(b) x = 1

Question 16.
The number of points in R in which the function f(x) = |x – 1| + |x – 3| + sin x is not differentiable is…………
(a) 3
(a) 2
(c) l
(d) 4
Solution:
(a) 2

Question 17.
If y = 1 + 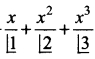 + …..∞ then \(\frac{dx}{dy}\) =……..
(a) x
(b) x²
(c) y
(d) y²
Solution:
(d) y²

Question 18.
\(\int \frac{\sqrt{\tan x}}{\sin 2 x}\) dx = …………….
(a) \(\sqrt{tan x}\) + c
(b) 2\(\sqrt{tan x}\) + c
(c) \(\frac{1}{2}\) \(\sqrt{tan x}\) + c
(d) \(\frac{1}{4}\) \(\sqrt{tan x}\) + c
Solution:
(a) \(\sqrt{tan x}\) + c

Question 19.
An urn contains 5 red and 5 black balls. A balls is drawn at random, its colour is noted and is returned to the um. Moreover, 2 additional balls of the colour drawn are put in the urn and then a ball is drawn at random. The probability that the second ball drawn is red will be ………….
(a) \(\frac{5}{12}\)
(b) \(\frac{1}{2}\)
(c) \(\frac{7}{12}\)
(d) \(\frac{1}{4}\)
Solution:
(b) \(\frac{1}{2}\)

Question 20.
A bag contains 6 green, 2 white, and 7 black balls. If two balls are drawn simultaneously then the probability that both are different colours is……….
(a) \(\frac{68}{105}\)
(b) \(\frac{71}{105}\)
(c) \(\frac{64}{105}\)
(d) \(\frac{73}{105}\)
Solution:
(a) \(\frac{68}{105}\)

PART – II

II. Answer any seven questions. Question No. 30 is compulsory. [7 × 2 = 14]

Question 21.
On the set of natural numbers let R be the relation defined by aRb if 2a + 3b = 30. Write down the relation by listing all the pairs. Check whether it is (i) reflexive, (ii) symmetric, (iii) transitive, (iv) equivalence
Solution:
N = {set of natural numbers};
R ={(3,8), (6, 6), (9, 4), (12, 2)}
(3, 3) ∉ R ⇒ R is not reflexive
(3, 8) ∈ R (8, 3) ∉ R
2a + 3b = 30
3b = 30 – 2a
b = \(\frac{30-2a}{3}\)
⇒ R is not symmetric
(a, b) (b, c) ∉ R ⇒ R is transitive
∴ It is not equivalence relation.

Question 22.
Compute log₉27 – log₂₇9.
Solution:
Let log₉27 = x ⇒ 27 = 9^x ⇒ 3³ = (3²)^x = 3^2x
⇒ 2x = 3 ⇒ x = 3/2
Let log₂₇ 9 = x
9 = 27^x
3² = (3³)^x ⇒ 3² = 3^3x
3x = 2 ⇒ x = 2/3
∴ log₉27 – log₂₇9 = \(\frac{3}{2}\) – \(\frac{2}{3}\) = \(\frac{9-4}{6}\) = \(\frac{5}{6}\)

Question 23.
Write the first 6 terms of the exponential series e^5x
Solution:

Question 24.
Find the points on the line x + y = 5, that lie at a distance 2 units from the line 4x + 3y – 12 = 0.
Solution:
Any point on the line x + y = 5 is x = t, y = 5 – t
The distance from (t, 5 – t) to the line 4x.+ 3y – 12 = 0 is given by 2 units.
∴ \(\frac{4(t)+3(5-t)-12}{\sqrt {4^2+3^2}}\) = 2 ⇒ \(\frac{|t+3|}{5}\) = 2
⇒ t + 3 = ± 10
t = -13, t = 7
∴ The points (-13, 18) and (7, -2).

Question 25.
Find |\(\vec{a}\) × \(\vec{b}\)| where \(\vec{a}\) = 3\(\vec{i}\) + 4\(\vec{j}\) and \(\vec{b}\) = \(\vec{i}\) +\(\vec{j}\) + \(\vec{k}\)
Solution:
\(\vec{a}\) × \(\vec{b}\) = \(\left|\begin{array}{lll} \hat{i} & \hat{j} & \hat{k} \\ 3 & 4 & 0 \\ 1 & 1 & 1 \end{array}\right|\) = \(\hat{i}\)(4 – 0) – \(\hat{j}\)(3 – 0) + \(\hat{k}\){3 – 4) = 4\(\hat{i}\) – 3\(\hat{j}\) – \(\hat{k}\)
|\(\vec{a}\) × \(\vec{b}\)| = |4\(\hat{i}\) – 3\(\hat{j}\) – \(\hat{k}\)| = \(\sqrt{16+9+1}\) = \(\sqrt{26}\)

Question 26.
Evaluate \(\lim _{x \rightarrow 1} \frac{x^{m}-1}{x^{n}-1}\) m and n are integers.
Solution:

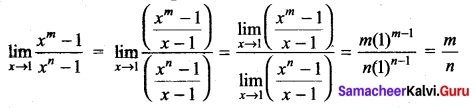
Question 27.
Find the derivative of sinx² with respect to x²
Solution:
Here u = sinx² and v = x²
Now we have to find

Question 28.
Evaluate ∫[5x⁴ + 3(2x + 3)⁴ – 6(4 – 3x)⁵]
Solution:
∫[5 x⁴ + 3(2x + 3)⁴ – 6(4 – 3x)⁵] dx.
= 5∫x⁴dx + 3∫ (2x + 3)⁴ dx – 6∫ (4 – 3x)⁵ dx
= 5.\(\frac{x^5}{5}\) + 3.\(\frac{1}{2}\)\(\frac{(2x+3)^5}{5}\) – 6.\(\frac{1}{(-3)}\)\(\frac{(4-3x)^6}{6}\) + c.
= x⁵ + \(\frac{3}{10}\)(2x + 3)⁵ + \(\frac{1}{3}\) (4 – 3x)⁶ + c

Question 29.
Given that P(A) = 0.52, P(B) = 0.43, and P(A ∩ B) = 0.24, find P(A ∪ B)
Solution:
P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
= 0.52 + 0.43 – 0.24
P(A ∪ B) = 0.71

Question 30.
For what value of x, the matrix A = \(\left[\begin{array}{rrr} 0 & 1 & -2 \\ -1 & 0 & x^{3} \\ 2 & -3 & 0 \end{array}\right]\) is skew-symmetric.
Solution:

-x³ = -3 ⇒ x³ = 3 ⇒ x = 3^1/3

PART- III

III. Answer any seven questions. Question No. 40 is compulsory. [7 × 3 = 21]

Question 31.
Find the largest possible domain for the real valued function given by f(x) =\(\frac{\sqrt{9-x^{2}}}{\sqrt{x^{2}-1}}\)
Solution:
If x < -3 or x > 3, then x² will be greater than 9 and hence 9 – x² will become negative which has no square root in R. So x must lie on the interval [-3, 3].
Also if x ≥ – 1 and x ≤ 1, then x² – 1 will become negative or zero. If it is negative, x² – 1^e has no square root in R. If it is zero, f is not defined. So x must lie outside [-1, 1]. That is, x must lie on (- ∞, -1) ∪ (1, ∞). Combining these two conditions, the largest possible domain for/is [-3, 3] ∩ ((-∞, -1) ∪ (i, ∞)). That is, [-3, -1) ∪ (1, 3].

Question 32.
Solve sin x + sin 5x = sin 3x
Solution:
sin x + sin 5x = sin 3x ⇒ 2 sin 3x cos 2x = sin 3x
sin 3x (2 cos 2x – 1) = 0
Thus, either sin 3x = 0 (or) cos 2x = \(\frac{1}{2}\)
If sin 3x = 0, then 3x = nπ ⇒ x = \(\frac{nπ}{3}\) n ∈ Z ………(i)
If cos 2x = \(\frac{1}{2}\) ⇒ cos 2x = cos \(\frac{π}{3}\)
2x = 2nn ± \(\frac{π}{3}\) ⇒ x = nπ ± \(\frac{π}{6}\), n ∈ Z ….(ii)
From (i) and (ii), we have the general solution x = \(\frac{π}{3}\) (or) x = nπ ± \(\frac{π}{6}\), n ∈ Z

Question 33.
How many triangles can be formed by 15 points in which 7 of them lie on one line and the remaining 8 on another parallel line?
Solution:

7 points lie on one line and the other 8 points parallel on another parallel line.
A triangle is obtained by taking one point from one line and 2 points from the other parallel line which can be done as follows.
⁷C₁ × ⁸C₂ or ⁷C₂ × ⁸C₁
⁷C₁ = 7; ⁷C₂ = \(\frac{7×6}{2×1}\) = 21
⁸C₁ = 8; ⁸C₂= \(\frac{8×7}{2×1}\) = 28
∴ No. of triangles = (7) (28) + (21) (8) = 196 + 168 = 364

Question 34.
Using binomial theorem indicate which of the following two numbers is larger (1.01)^1000000 or 10000
Solution:
(1.01)^1000000 = (1 + 0.01)^1000000
= ^1000000C₀(1)^1000000 + ^1000000C₁(1)⁹⁹⁹⁹⁹⁷(0.01)¹
+ ^1000000C₂(1)⁹⁹⁹⁹⁹⁸(0.01)² + ^1000000C₃(1)⁹⁹⁹⁹⁹⁷(0.01)³ +……….
= 1 (1) + 1000000 × \(\frac{1}{10^2}\) + \(\frac{1000000×999999}{2}\) × \(\frac{1}{10000}\) + …………
= 1 + 10000 + 50 × 999999 +…………
which is > 10000
So (1.01)^1000000 > 10000 (i.e.) (1.01)^1000000 is larger.

Question 35.
If a line joining two points (3, 0) and (5, 2) is rotated about the point (3, 0) in counter clockwise direction through an angle 15°, then find the equation of the line in the new position.
Solution:

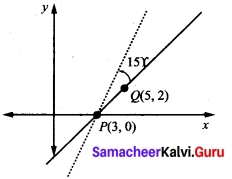
Let P (3, 0) and Q (5, 2) be the given points.
Slope of PQ = \(\frac{y_2-y_1}{x_2-x_1}\) = 1
⇒ The angle of inclination of the line PQ = tan^-1(1) = \(\frac{π}{4}\) = 45°
∴ The slope of the line in new position is m = tan (45° + 15°)
⇒ Slope = tan (60°) = (√3)
∴ Equation of the straight line passing through (3, 0) and with the slope √3 is y – 0 = √3 (x – 3)
√3 x – y – 3√3 = 0

Question 36.
Find the area of the triangle whose vertices are A(3, -1, 2), B(l, -1, -3) and C(4, -3,1)
Solution:
A = (3, -1, 2), B = (1, -1, -3) and C = (4, -3, 1)
∴ \(\vec{OA}\) = 3\(\hat{i}\) – \(\hat{j}\) + 2\(\hat{k}\); \(\vec{OB}\) = \(\hat{i}\) – \(\hat{j}\) – 3\(\hat{k}\); and \(\vec{OC}\) = 4\(\hat{i}\) – 3\(\hat{j}\) + \(\hat{k}\)
Area of ΔABC = \(\frac{1}{2}\)|\(\vec{AB}\) × \(\vec{AC}\)| = \(\frac{1}{2}\)|\(\vec{BA}\) × \(\vec{BC}\)| = \(\frac{1}{2}\)|\(\vec{CA}\) x \(\vec{CB}\)|
\(\vec{AB}\) = \(\vec{OB}\) – \(\vec{OA}\) = (\(\hat{i}\) – \(\hat{j}\) – 3\(\hat{k}\)) – (3\(\hat{i}\) – \(\hat{j}\) + 2\(\hat{k}\)) = \(\hat{i}\) – \(\hat{j}\) – 3\(\hat{k}\) – 3\(\hat{i}\) + \(\hat{j}\) – 2\(\hat{k}\)
= -2\(\hat{i}\) – 5\(\hat{k}\)
\(\vec{AC}\) = \(\vec{OC}\) – \(\vec{OA}\) = 4\(\hat{i}\) – 3\(\hat{j}\) + \(\hat{k}\) – 3\(\hat{i}\) + \(\hat{j}\) – 2\(\hat{k}\)
= \(\hat{i}\) – 2\(\hat{j}\) – \(\hat{k}\)

Question 37.
Check if \(\lim _{x \rightarrow-5}\) f(x) exists or not, where f(x) = \(\left\{\begin{array}{l} \frac{|x+5|}{x+5}, \text { for } x \neq-5 \\ 0, \quad \text { for } x=-5 \end{array}\right.\)
Solution:
(i) f(-5^–)
For x < -5, |x + 5| = -(x + 5)
Thus f(-5^–) = \(\lim _{x \rightarrow-5^-}\) \(\frac{-(x-5)}{(x+5)}\) = -1

(ii) f(-5⁺)
For x > -5, |x + 5| = (x + 5)
Thus f(-5⁺) = \(\lim _{x \rightarrow-5^+}\) \(\frac{(x+5)}{(x+5)}\) = 1
∴ f(-5^–) ≠ f(-5⁺). Hence the limit does not exist.

Question 38.
Evaluate \(\frac{\sqrt{x}}{1+\sqrt{x}}\)
Solution:

Question 39.
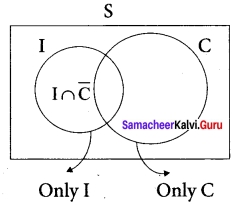
The probability that a girl, preparing for competitive examination will get a State Government service is 0.12, the probability that she will get a Central Government job is 0.25, and the probability that she will get both is 0.07. Find the probability that
(i) she will get atleast one of the two jobs
(ii) she will get only one of the two jobs.
Solution:
Let I be the event of getting State Government service and C be the event of getting Central Government job.
Given that P(I) = 0.12, P(C) = 0.25, and P(I ∩ C) = 0.07
(i) P (at least one of the two jobs) = P(I or C) = P(I ∪ C)
= P(I) + P(C) – P(I ∩ C)
= 0.12 + 0.25 – 0.07 = 0.30

(if) P(only one of the two jobs) = P[only I or only C].
= P(I ∩ \(\bar{C}\)) + P(\(\bar{I}\) ∩ C)
= (P(I) – P(I ∩ C)} + (P(C) – P(I ∩ C)}
= {0.12 – 0.07} + {0.25 – 0.07}
= 0.23.

Question 40.
Find the derivatives of the following function. \(\sqrt{xy}\) = e^(x-y)
Solution:
\(\sqrt{xy}\) = e^x-y
(i.e.) (xy)^1/2 = e^x-y
Taking log on both sides we get
log (xy)^1/2 = log e^x-y
(i.e.) \(\frac{1}{2}\) (log x + log y) = x – y
⇒ log x + log y = 2x – 2y
differentiating w.r. to x we get

PART – IV

IV. Answer all the questions. [7 × 5 = 35]

Question 41 (a).
Find the range of the function \(\frac{1}{2cos x -1}\)
Solution:
The range of cos x is – 1 to 1
-1 < cos x < 1
(× by 2) -2 < 2 cos x < 2
adding -1 throughout
-2 – 1 <2 cos x – 1 < 2 – 1
(i.e.,) -3 < 2 cos x – 1 < 1
so 1 < \(\frac{1}{2cos x -1}\) < \(\frac{-1}{3}\)
The range is outside \(\frac{-1}{3}\) and 1
i.e., range is (-∞, \(\frac{-1}{3}\)] ∪ [1, ∞)

[OR]

(b) Solve \(\frac{(x-2)}{(x+4)}\) ≥ \(\frac{5}{(x+3)}\)
Solution:

x + 4 = 0 ⇒ x = -4; x + 3 = 0 ⇒ x = -3
Plotting the points -4, -3 on number line and taking limits (-∞, -4), (-4, -3), (-3, ∞)

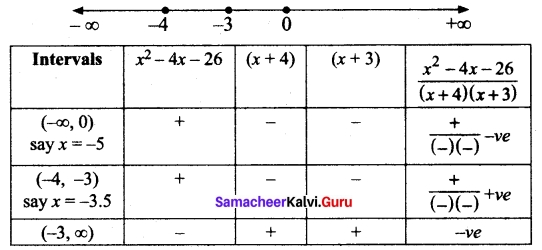
The solution for the inequality \(\frac{(x-2)}{(x+4)}\) ≥ \(\frac{5}{(x+3)}\) are the intervals (-∞, -4) and (-4, -3)

Question 42 (a).
Prove that log 2 + 16 log \(\frac{16}{15}\) + 12 log \(\frac{25}{24}\) + 7 log \(\frac{80}{81}\) = 1
Solution:
LHS = log 2 + 16 [log 16 – log 15] + 12 [log 25 – log 24] + 7 [log 81 – log 80]

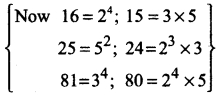
= log 2 + 16 [log 2⁴ – log 3 × 5 ] + 12 [log 5² – log 2³ × 3] + 7[log 3⁴ – log 2⁴ × 5]
= log 2 + 16 [41og2 – log3 – log5] + 12 [2 log 5 – 3 log 2 – log 3] + 7 [4 log 3 – 4 log 2 – log 5]
= log 2 + 64 log 2 – 16 log 3 – 16 log 5 + 24 log 5 – 36 log 2 – 12 log 3 + 28 log 3 – 28 log 2 – 7 log 5
= log 2 [1+ 64 – 36 – 28] + log 3 [-16 – 12 + 28] + log 5 [-16 + 24 – 7]
= log 2(1) + log 3(0) +log 5(1)
= log 2 + log 5 = log 2 × 5 = log 10 = 1 = RHS

[OR]

(b) If tan α = \(\frac{1}{3}\) and tan β = \(\frac{1}{7}\) show that 2 α + β = \(\frac{π}{4}\)
Solution:

∴ 2 α + β = 45° = \(\frac{π}{4}\)

Question 43 (a).
Using Binomial theorem, prove that 6ⁿ – 5n always leaves remainder 1 when divided by 25 for all positive integer n.
Solution:
To prove this it is enough to prove, 6ⁿ – 5n = 25k + 1 for some integer k. We first consider the expansion
(1 + x)ⁿ = ⁿC₀ + ⁿC₁ x + ⁿC₂ x² +…+ ⁿC_n-1x^n-1 + ⁿC_n xⁿ, n ∈ N.
Taking x = 5 we get (1 + 5)ⁿ = ⁿC₀ + ⁿC₁ 5 + ⁿC₂ 5² +…+ ⁿC_n-1 5^n-1 + ⁿC_n 5ⁿ. The above equality reduces to 6ⁿ = 1 + 5n + 25(ⁿC₂ + 5 ⁿC₃ +…+ ⁿC_n 5^n-2)
That is,
6ⁿ – 5n = 1 + 25(ⁿC₂ + 5 ⁿC₃ +…+ ⁿC_n 5^n-2) = 1 + 25k, k ∈ N.
Thus 6ⁿ – 5n always, leaves remainder 1 when divided by 25 for all positive integer n.

[OR]

(b) Prove that

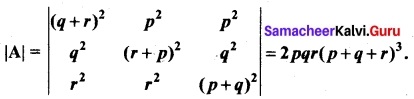
Solution:
Taking p = 0, we get |A| = \(\left|\begin{array}{ccc} (q+r)^{2} & 0 & 0 \\ q^{2} & r^{2} & q^{2} \\ r^{2} & r^{2} & q^{2} \end{array}\right|\) = 0
Therefore, (p- 0) is a factor. That is, p is a factor.
Since |A| is in cyclic symmetric form in p, q, r and hence q and r also factors.
Putting p + q + r = 0 ⇒ q + r = -p; r + p = -q; and p + q = -r.
|A| = \(\left|\begin{array}{lll} p^{2} & p^{2} & p^{2} \\ q^{2} & q^{2} & q^{2} \\ r^{2} & r^{2} & r^{2} \end{array}\right|\) = 0 since 3 columns are identical.
Therefore, (p + q + r)² is a factor of |A|.
The degree of the obtained factor pqr(p + q + r)² is 5. The degree of |A| is 6.
Therefore required factor is k (p + q + r)

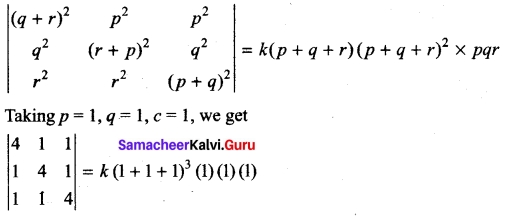
4(16 – 1) -1 (4 – 1) +1 (1 – 4) = 27k
60 – 3 – 3 = 27 k ⇒ k = 2.
|A| = 2pqr (p + q + r)³

Question 44 (a).
The sum of the distance of a moving point from the points (4, 0) and (-4, 0) is always 10 units. Find the equation of the locus of the moving point.
Solution:
Let point (h, k) be a moving point
Here A = (4, 0) and B = (- 4, 0)
Given PA + PB = 10
⇒ \(\sqrt{(h-4)^{2}+k^{2}}+\sqrt{(h+4)^{2}+k^{2}}\) = 10
⇒ \(\sqrt{(h-4)^{2}+k^{2}}\) = 10 – \(\sqrt{(h+4)^{2}+k^{2}}\)
Squaring both sides (h – 4)² + k² = 100 + (h + 4)² + k² – 20\(\sqrt{(h+4)^{2}+k^{2}}\)
(i.e.) h² + l6 – 8h + k² = 100 + h² + 16 + 8h + k² – 20\(\sqrt{(h+4)^{2}+k^{2}}\)
⇒ -16h – 100 = – 20 \(\sqrt{(h+4)^{2}+k^{2}}\)
(÷ by -4) 4h + 25 = 5 \(\sqrt{(h+4)^{2}+k^{2}}\)
Squaring both sides we get,
(4h + 25)² = 25 [(h + 4)² + k²]
(i.e) 16h² + 25 + 200h = 25 [h² + 8h + 16 + k²]
= 16h² + 625 + 200h – 25h² – 200h – 400 – 25k² = 0
= – 9h² – 25k² + 225 = 0
⇒ 9h² + 25 k² = 225
\(\frac{9h^2}{225}\) + \(\frac{25k^2}{225}\) = 1
(i.e) h²/25 + k²/9 = 1, So the locus is \(\frac{x^2}{25 }\) + \(\frac{y^2}{9}\) = 1

[OR]

(b) Show that the vectors \(\hat{i}\) – 2\(\hat{j}\) + 3\(\hat{k}\), -2\(\hat{i}\) + 3\(\hat{j}\) – 4\(\hat{k}\) and – \(\hat{j}\) + 2\(\hat{k}\) are coplanar.
Solution:
Let the given three vectors be \(\vec{a}\), \(\vec{b}\) and \(\vec{c}\). When we are able to write one vector as a linear combination of the other two vectors, then the given vectors are called coplanar vectors.
Let \(\vec{a}\) = m\(\vec{b}\) + n\(\vec{c}\) where
(i.e.) \(\vec{a}\) = \(\hat{i}\) – 2\(\hat{j}\) + 3\(\hat{k}\)
\(\vec{b}\) = -2\(\hat{i}\) + 3\(\hat{j}\) – 4\(\hat{k}\) and \(\vec{c}\) = –\(\hat{j}\) + 2\(\hat{k}\)
⇒ \(\hat{i}\) – 2\(\hat{j}\) + 3\(\hat{k}\) = m (-2\(\hat{i}\) + 3\(\hat{j}\) – 4\(\hat{k}\)) + n (-\(\hat{j}\) + 2\(\hat{k}\))
Equating the \(\hat{i}\), \(\hat{j}\) and \(\hat{k}\) components
(i.e.) 1 = -2m ……… (1)
-2 = 3m – n …………(2)
3 = -4m + 2n …………(3)
Now we have to solve (1) and (2) and substitute the value in (3).
Solving (1) and (2)
(1) ⇒ -2m = 1
∴ m = –\(\frac{1}{2}\)
Substituting m = –\(\frac{1}{2}\) in (2) we get,
3(\(\frac{-1}{2}\)) – n = -2
–\(\frac{3}{2}\) – n = -2
∴ -n = -2 + \(\frac{3}{2}\) = \(\frac{-4+3}{2}\) = –\(\frac{1}{2}\)
n = \(\frac{1}{2}\)
∴ m = –\(\frac{1}{2}\); n = \(\frac{1}{2}\)
Substituting the values of m and n in (3).
LHS = 3
RHS = -4 + 2n = -4(\(\frac{-1}{2}\)) + 2(\(\frac{1}{2}\))
= 2 + 1 = 3
⇒ LHS = RHS
∴ we are able to write one vector as a linear combination of the other two
⇒ the given vectors are coplanar.

Question 45 (a).
A committee of 7 peoples has to be formed from 8 men and 4 women. In how many ways can this be done when the committee consists of
(i) exactly 3 women?
(ii) at least 3 women?
(iii) at most 3 women?
Solution:

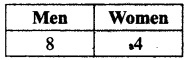
We need a committee of 7 people with 3 women and 4 men.
This can be done in (⁴C₃) (⁸C₄) ways
⁴C₁ = ⁴C₁ = 4
⁸C₄ = \(\frac{8×7×6×5}{4×3×2×1}\) = 70
The number of ways = (70) (4) = 280

(ii) Atleast 3 women

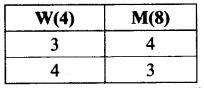
So the possible ways are (3W and 4M) or (4W and 3M)
(i.e) (⁴C₃) (⁸C₄) + (⁴C₄) (⁸C₃)
⁴C₃ = ⁴C₁ = 4; ⁴C₄ = 1
⁸C₄ = \(\frac{8×7×6×5}{4×3×2×1}\) = 70
⁸C₃ = \(\frac{8×7×6}{3×2×1}\) = 56
The number of ways (4) (70) + (1) (56) = 280 + 56 = 336

(iii) Atmost 3 women

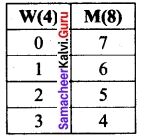
The possible ways are (0W 8M) or (1W 6M) or (2W 5M) or (3W 4M)

∴ The possible ways are
(1) (8) + (4) (28) + (6) (56) + (4) (70) = 8 + 112 + 336 + 280 = 736 ways

[OR]

(b) Evaluate \(\lim _{x \rightarrow 0} \frac{\sqrt{1+\sin x}-\sqrt{1-\sin x}}{\tan x}\)
Solution:

Question 46 (a).
If y = \(\frac{\sin ^{-1} x}{\sqrt{1-x^{2}}}\) show that (1 – x²)y₂ – 3xy₁ – y = 0
Solution:
y = \(\frac{\sin ^{-1} x}{\sqrt{1-x^{2}}}\)
⇒ y \(\sqrt{1-x^2}\) = sin^-1 x
differentiating w.r.to x we get

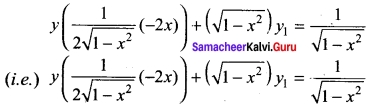
multiplying both sides by \(\sqrt{1-x^2}\) we get
-xy + (1 – x²)y₁ = 1
differentiating both sides again w.r.to x.
– [xy^-1 +y(1)] + (1 – x²) (y₂) + y₁(-2x) = 0
(i.e.) -xy₁ – y + (1 – x²)y₂ – 2xy₁ = 0
(1 – x²)y₂ – 3xy₁ – y = 0

[OR]

(b) If y = cos (m sin^-1 x), prove that (1 – x²) y₃ – 3xy₂ + (m² – 1) y₁ = 0
Solution:
We have y = cos (m sin^-1 x)
y₁ = sin(m sin^-1 x) \(\frac{m}{\sqrt{1-x^2}}\)
\(y_{1}^{2}\) = sin² (m sin^-1 x) \(\frac{m^2}{(1-x^2)}\)
This implies (1 – x²) \(y_{1}^{2}\) = m² sin² (m sin^-1 x) = m² [1 – cos² (m sin^-1 x)]
This is, (1 – x²) \(y_{1}^{2}\) = m² (1 – y²).
Again differentiating,
(1 – x²) 2y₁ \(\frac{dy_1}{dx}\) + \(y_{1}^{2}\)(-2x) = m² (-2y\(\frac{dy}{dx}\))
(1 – x²) 2y₁y₂ – 2x\(y_{1}^{2}\) = – 2m²yy₁
(1 – x²) y₂ – xy₁ = m²y
Once again differentiating
(1 – x²) 2y₁ \(\frac{dy_2}{dx}\) + \(y_{2}\)(-2x) – [x.\(\frac{dy_1}{dx}\) + y₁.1] = -m² (\(\frac{dy}{dx}\))
(1 – x²)y₃ – 2xy₂ – xy₂ – y₁ = -m²y₁
(1 – x²)y₃ – 3xy₂ + (m² – 1)y₁ = 0

Question 47 (a).
Evaluate ∫\(\frac{dx}{\sqrt{9+8x-x^2}}\)
Solution:
Let I = ∫\(\frac{dx}{\sqrt{9+8x-x^2}}\) dx
Consider, 9 + 8x – x²
= -[x² – 8x – 9]
= -[(x – 4)² – 16 – 9]
= -[(x – 4)² – (5)²]
= (5)² – (x – 4)²

[OR]

(b) An advertising executive is studying television viewing habits of married men and women during prime time hours. Based on the past viewing records he has determined that during prime time wives are watching television 60% of the time. It has also been determined that when the wife is watching television, 40% of the time the husband is also watching. When the wife is not watching the television, 30% of the time husband is watching the television. Find the probability that
(i) the husband is watching the television during the prime time of television
(ii) if the husband is watching the television, the wife is also watching the television.
Solution:
P(Wife watching TV) = P(W) = \(\frac{60}{100}\)
P(H/W) = \(\frac{40}{100}\); P(H/W’) = 30/100
(i) P(Husband watching TV) = P(H)
= P(H/W) P(W) + P(H/W’) P(W’)