You can Download Samacheer Kalvi 9th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 2 Real Numbers Additional Questions
Exercise 2.1
Question 1.
Find only two rational numbers between \(\frac { 1 }{ 4 }\) and \(\frac { 3 }{ 4 }\).
Solution:
A rational number between \(\frac { 1 }{ 4 }\) and \(\frac { 3 }{ 4 }\) = \(\frac { 1 }{ 2 }\) ( \(\frac { 1 }{ 4 }\) + \(\frac { 3 }{ 4 }\)) = \(\frac { 1 }{ 2 }\) (1) = \(\frac { 1 }{ 2 }\)
Another rational number between \(\frac { 1 }{ 2 }\) and \(\frac { 3 }{ 4 }\) = \(\frac { 1 }{ 2 }\) ( \(\frac { 1 }{ 2 }\) + \(\frac { 3 }{ 4 }\)) = \(\frac { 1 }{ 2 }\) ( \(\frac { 2+3 }{ 4 }\) = \(\frac { 31}{ 2 }\) × \(\frac { 5 }{ 4 }\)) = \(\frac { 5 }{ 8 }\)
The rational numbers \(\frac { 1 }{ 2 }\) and \(\frac { 5 }{ 8 }\) lies between \(\frac { 1 }{ 4 }\) and \(\frac { 3 }{ 2 }\) .
Question 2.
Is zero a rational numbers? Give reasons for your answer.
Solution:
Yes, since \(\frac { 0 }{ 2 }\) = 0, (i.e) it can be written in the form \(\frac { p }{ q }\) where q ≠ 0
![]()
Exercise 2.2
That’s literally all there is to it! 9/20 as a decimal is 0.45
Question 1.
Express the following decimal expansion is the form \(\frac { p }{ q }\) , where p and q are integers and q ≠ 0.
(i) 0.75
(ii) 0.625
(iii) 0.5625
(iv) 0.28
Solution:

Question 2.
Convert \(\overline { 0.9 }\) to a rational number.
Solution:
(i) Let x = \(0.\overline { 9 }\). Then x = 0.99999….
Multiplying by 10 on both sides, we get
10x = 9.99999….. = 9 + 0.9999….. = 9 + x
9x = 9
x = 1. That is, \(0.\overline { 9 }\) = 1 (∵ 1 is rational number).
Exercise 2.3
Question 1.
Classify the following number as rational or irrational.
(i) \(\sqrt { 11 }\)
(ii) \(\sqrt { 81 }\)
(iii) 0.0625
(iv) \(0.8\overline { 3 }\)
Solution:
(i) \(\sqrt { 11 }\) is an irrational number. (11 is not a perfect square number)
(ii) \(\sqrt { 81 }\) = 9 = \(\frac { 9 }{ 1 }\) , a rational number.
(iii) 0.0625 is a terminating decimal
∴ 0. 0625 is a rational number.
(iv) \(0.8\overline { 3 }\) = 0.8333
The decimal expansion is non-terminating and recurring.
∴ \(0.8\overline { 3 }\) is a rational number.
Question 2.
Find the decimal expansion of \(\sqrt { 3 }\).
Solution:

Question 3.
Find any 4 irrational numbers between \(\frac { 1 }{ 4 }\) and \(\frac { 1 }{ 3 }\).
Solution:
\(\frac { 1 }{ 4 }\) = 0.25 and \(\frac { 1 }{ 3 }\) = 0.3333 = \(0.\overline { 3 }\)
In between 0.25 and \(0.\overline { 3 }\) there are infinitely many irrational numbers .
Four irrational numbers between 0.25 and \(0.\overline { 3 }\) are
0.2601001000100001 ……
0.2701001000100001 ……
0.2801001000100001 …..
0.3101001000100001 ……
![]()
Exercise 2.4
Question 1.
Visualise \(6.7\overline { 3 }\) on the number line, upto 4 decimal places.
Solution:
We locate 6.73 on the number line, by the process of successive magnification.
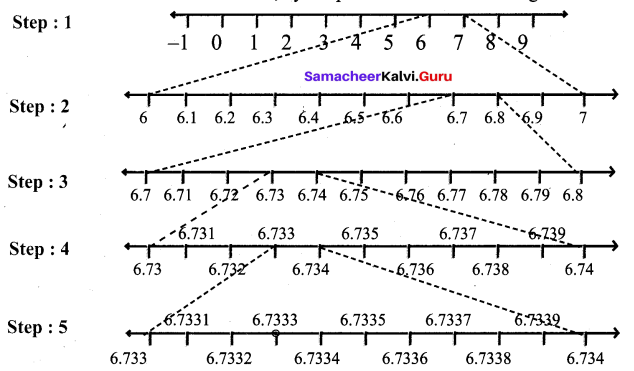
Step 1 : First we note that \(6.7\overline { 3 }\) lies between 6 and 7.
Step 2 : Divide the portion between 6 and 7 into 10 equal parts and use a magnifying glass to visualise that \(6.7\overline { 3 }\) lies between 6.7 and 6.8.
Step 3 : Divide the portion between 6.7 and 6.8 into 10 equal parts and use a magnifying glass to visualise that \(6.7\overline { 3 }\) lies between 6.73 and 6.74.
Step 4 : Divide the portion between 6.73 and 6.74 into 10 equal parts and use a magnifying glass to visualise that \(6.7\overline { 3 }\) lies between 6.733 and 6.734.
Step 5 : Divide the portion between 6.733 and 6.734 into 10 equal parts and use a magnifying glass to visualise that \(6.7\overline { 3 }\) lies between 6.7332 and 6.7334.
We note that \(6.7\overline { 3 }\) is visualised closed to 6.7332 than to 6.7334.
Question 2.
Find whether x and y are rational or irrational in the following:
(i) a = 2 + \(\sqrt{3}\), b = 2 – \(\sqrt{3}\); x = a + b, y = a – b
(ii) a = \(\sqrt{2}\) + 7, b = x = a + b, y = a – b
Solution:
(i) Given that a = 2 + \(\sqrt{3}\), b = 2 – \(\sqrt{3}\)
x = a + b = (2+ \(\sqrt{3}\)) +(2 – \(\sqrt{3}\)) = 4, a rational number.
y = a – b = {2 + \(\sqrt{3}\)) – (2 – \(\sqrt{3}\)) = 2\(\sqrt{3}\) , an irrational number.
(ii) Given that a = \(\sqrt{2}\) + 7,b = \(\sqrt{2}\) – 7
x = a + b = (\(\sqrt{2}\) + 7)+ (\(\sqrt{2}\) – 7) = 2\(\sqrt{2}\), an irrational number.
y = a – b = (\(\sqrt{2}\) + 7 ) – (\(\sqrt{2}\) – 7) = 14, a rational number.
Exercise 2.5
Question 1.
Evaluate :
(i) 10-4
(ii) (\(\frac { 1 }{ 9 }\))-3
(iii) (0.01)-2
Solution:
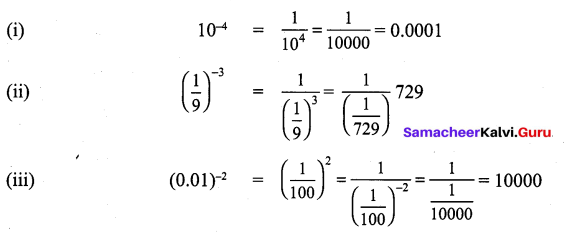
Question 2.
Find the value of 625\(\frac { 3 }{ 4 }\) :
Solution:
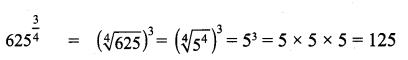
Question 3.
Find the value of 729\(\frac { -5 }{ 6 }\) :
Solution:
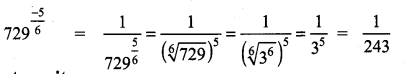
Question 4.
Use a fractional index to write :
(i) (5\(\sqrt { 125 }\))7
(ii) \(\sqrt [ 3 ]{ 7 }\)
Solution:
(i) (5\(\sqrt { 125 }\))7 = 125\(\frac { 7 }{ 5 }\)
(ii) \(\sqrt [ 3 ]{ 7 }\) = 7\(\frac { 1 }{ 3 }\)
![]()
Exercise 2.6
Question 1.
Can you reduce the following numbers to surds of same order.
(i) \(\sqrt{ 5 }\)
(ii) \(\sqrt [ 3 ]{ 5 }\)
(iii) \(\sqrt [ 4 ]{ 5 }\)
Solution:
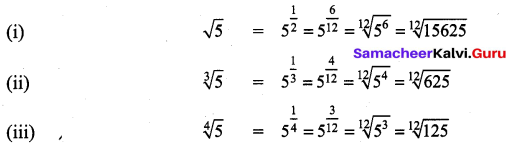
Now the surds have same order
Question 2.
Express the following surds in its simplest form
(i) \(\sqrt { 27 }\)
(ii) \(\sqrt [ 3 ]{ 128 }\)
Solution:
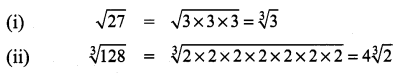
Question 3.
Show that \(\sqrt [ 3 ]{ 2 }\) > \(\sqrt [ 5 ]{ 3 }\).
Solution:
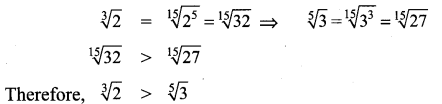
Question 4.
Express the following surds in its simplest form \(\sqrt [ 4 ]{ 324 }\).
Solution:
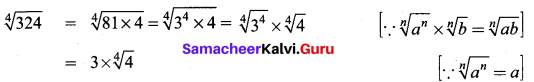
order = 4 ; radicand = 4; Coefficient = 3
![]()
Question 5.
Simplify \(\sqrt { 63 }\) – \(\sqrt { 175 }\) + \(\sqrt { 28 }\)
Solution:
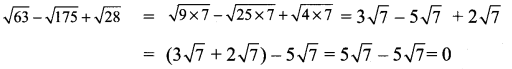
Question 6.
Arrange in ascending order: \(\sqrt [ 3 ]{ 2 }\), \(\sqrt [ 2 ]{ 4 }\), \(\sqrt [ 4 ]{ 3 }\)
Solution:
The order of the surds \(\sqrt [ 3 ]{ 2 }\), \(\sqrt [ 2 ]{ 4 }\), \(\sqrt [ 4 ]{ 3 }\) are 3, 2, 4
L.CM. of 3, 2, 4 = 12.
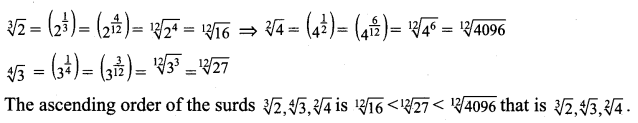
Exercise 2.7
Question 1.
Subtract 6\(\sqrt { 7 }\) from 9\(\sqrt { 7 }\). Is the answer rational or irrational?
Solution:
9\(\sqrt { 7 }\) – 6\(\sqrt { 7 }\) = (9 – 6) \(\sqrt { 7 }\) = 3\(\sqrt { 7 }\)
The answer is irrational.
Question 2.
Simplify,: \(\sqrt { 44 }\) + \(\sqrt { 99 }\) – \(\sqrt { 275 }\).
Solution:
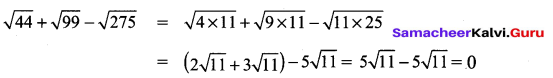
Question 3.
Compute and give the answer in the simplest form : 3 \(\sqrt { 162 }\) x 7 \(\sqrt { 50 }\) x 6 \(\sqrt { 98 }\)
Solution:
3 \(\sqrt { 162 }\) × 7 \(\sqrt { 50 }\) × 6 \(\sqrt { 98 }\) = \((3 \times 9 \sqrt{2} \times 7 \times 5 \sqrt{2} \times 6 \times 7 \sqrt{2})\)
= \(3 \times 7 \times 6 \times 9 \times 5 \times 7 \times \sqrt{2} \times \sqrt{2} \times \sqrt{2}=79380 \sqrt{2}\)
Exercise 2.8
Question 1.
Write in scientific notation : (60000000)3
Solution:
(60000000)3 = (6.0 × 107)4 = (6.0)4 × (107)4
= 1296 × 1028
= 1.296 × 103 × 1028 = 1.296 × 1031
Question 2.
Write in scientific notation : (0.00000004)3
Solution:
(0.00000004)3 = (4.0 × 10-8)3 = (4.0)3 × (10-8)3
= 64 × 10-24 = 6.4 × 10 × 10-24 = 6.4 × 10-23
Question 3.
Write in scientific notation : (500000)5 × (3000)3
Solution:
(500000)5 × (3000)3 = (5.0 × 105)3 × (3.0 × 103)3
= (5.0)2 × (105)2 × (3.0)3 × (103)3
= 25 × 1010 × 27 × 109 = 675 × 1019
= 675.0 × 1019 = 6.75 × 102 × 1019= 6.75 × 1021
Question 4.
Write in scientific notation : (6000000)3 ÷ (0.00003)2
Solution:
(6000000)3 + (0.00003)2 = (6.0 × 106)3 + (3.0 × 10-5)2
= (6.0 × 106)3 ÷ (3.0 × 10-5)2 = 216 × 1018 ÷ 9 × 10-10
= \(\frac{216 \times 10^{9}}{9 \times 10^{-10}}\)
= 24 × 1018 × 1010 = 24 × 1028
= 24.0 × 1028 = 2.4 × 10 × 1028 = 2.4 × 1029
![]()
Exercise 2.9
Multiple Choice Questions :
Question 1.
A number having non-terminating and recurring decimal expansion is
(1) an integer
(2) a rational number
(3) an irrational number
(4) a whole number
Solution:
(2) a rational number
Hint:
Irrational number have nonterminating and non recurring decimal expansion.
Question 2.
If a number has a non-terminating and non-recurring decimal expansion, then it is
(1) a rational number
(2) a natural number
(3) an irrational number
(4) an integer
Solution:
(3) an irrational number
Hint: Rational number gave terminating or recurring and non-terminating decimal expansion.
Question 3.
Decimal form of \(\frac { -3 }{ 4 }\) is
(1) -0.75
(2) -0.50
(3) -0.25
(4) -0.125
Solution:
(1) -0.75
Hint:
\(\frac { 1 }{ 4 }\) = 0.25; \(\frac {1 }{ 2 }\) = 0.5; \(\frac { 3 }{ 4 }\) = 0.75
![]()
Question 4.
Which one of the following has a terminating decimal expansion?

Solution:
(1) \(\frac { 5 }{ 32 }\)
Hint:
32 = 25 ⇒ \(\frac { 5 }{ 32 }\) has terminating decimal expansion
Question 5.
Which one of the following is an irrational number?
(1) π
(2) √9
(3) \(\frac { 1 }{ 4 }\)
(4) \(\frac { 1 }{ 5 }\)
Solution:
(1) π
Question 6.
Which one of the following are irrational numbers?
![]()
(a) (ii), (iii) and (iv)
(b) (i), (ii) and (iv)
(c) (i), (ii) and (iii)
(d) (i), (iii) and (iv)
Solution:
(d) (i), (iii) and (iv)
Hint:
\(\sqrt{4+\sqrt{25}}=\sqrt{9}=3 ; \sqrt{8-\sqrt[3]{8}}=\sqrt{8-2}=\sqrt{6}\)
Question 7.
Which of the following is not an irrational number?
(1) \(\sqrt {2}\)
(2) \(\sqrt {5}\)
(3) \(\sqrt {3}\)
(4) \(\sqrt {25}\)
Solution:
(4) \(\sqrt {25}\)
Question 8.
In simple form, \(\sqrt [ 3 ]{ 54 }\) is?
(1) 3 \(\sqrt [ 3 ]{ 2 }\)
(2) 3 \(\sqrt [ 3 ]{ 27 }\)
(3) 3 \(\sqrt [ 3 ]{ 2 }\)
(4) \(\sqrt { 3 }\)
Solution:
(1) 3 \(\sqrt [ 3 ]{ 2 }\)
Question 9.
\(\sqrt [ 3 ]{ 192 }\) + \(\sqrt [ 3 ]{ 24 }\)
(1) 3\(\sqrt [ 3 ]{ 6 }\)
(2) 6\(\sqrt [ 3 ]{ 3 }\)
(3) 3\(\sqrt [ 3 ]{ 216 }\)
(4) 3\(\sqrt [ 6 ]{ 216 }\)
Solution:
(2) 6\(\sqrt [ 3 ]{ 3 }\)
![]()
Question 10.
5\(\sqrt { 21 }\) × 6\(\sqrt { 10 }\)
(1) 30\(\sqrt { 210 }\)
(2) 30
(3) \(\sqrt { 210 }\)
(4) 210\(\sqrt { 30 }\)
Solution:
(1) 30\(\sqrt { 210 }\)
Text Book Activities
Activity – 1
Is it interesting to see this pattern? \(\sqrt{4 \frac{4}{15}}=4 \sqrt{\frac{4}{15}} \text { and } \sqrt{5 \frac{5}{24}}=5 \sqrt{\frac{5}{24}}\) Verify it. Can you frame 4 such new surds?
Solution:
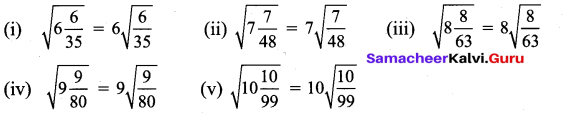
Activity – 2
Take a graph sheet and mark O, A, B, C as follows:

Consider the following graphs:
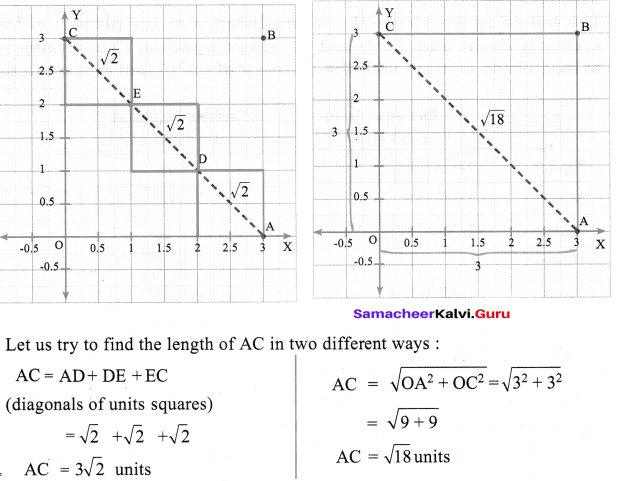
Are they equal? Discuss. Can you verify the same by taking different squares of different lengths?
Solution:

Activity – 3
The following list shows the mean distance of the planets of the solar system from the Sun. Complete the following table. Then arrange in order of magnitude starting with the distance of the planet closest to the Sun.
Solution:
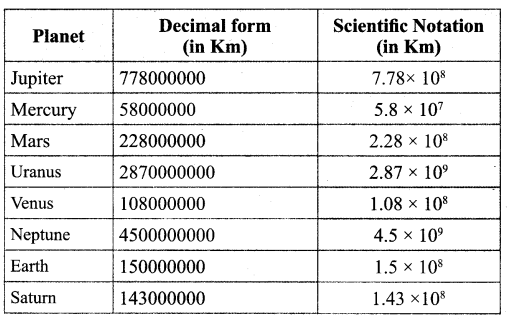
Arrange the planets in order of distance from the sun.
Mercury, Venus, Earth, Mars, Jupiter, Saturn, Uranus, Neptune and Pluto.