Students can Download Maths Chapter 3 Algebra Ex 3.1 Questions and Answers, Notes Pdf, Samacheer Kalvi 8th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 8th Maths Solutions Term 1 Chapter 3 Algebra Ex 3.1
![]()
Question 1.
Multiply a monomial by a monomial.
(i) 6x, 4
(ii) -3x, 7y
(iii) -2m2, (-5m)3
(iv) a3, – 4a2b
(v) 2p2q3, -9pq2
Solution:
(i) 6x × 4 = (6 × 4) (x) = 24x
(ii) -3x × 7y = (-3 × 7) (x × y) = -21xy
(iii) (-2m2) × (-5m)3 = -2m2 × (-)3 (53 (m)3) = -2m2 × (-125m3)
= (-) × (-)(2 × 125)(m2 × m3) = + 250m5 = 250 m
(iv) a3 × (-4a2 b) = (-4) × (a3 × a2) × (b) = -4a5b
(v) (2p2q3) × (-9pq2) = (+) × (-) × (2 × 9) (p2 × p(q3 × q2)) = -18p3q5
Question 2.
Complete the table
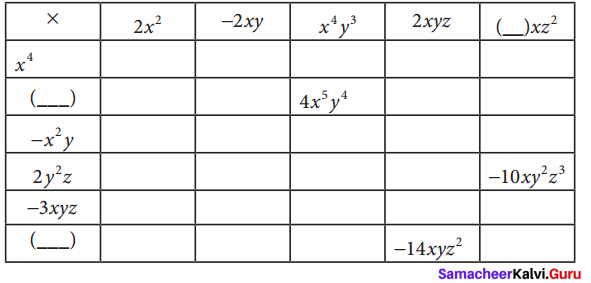
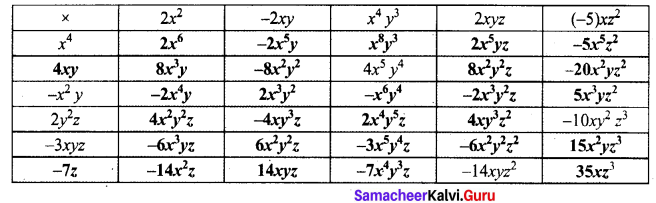
Solution:
Question 3.
Find the product of the terms.
(i) -2mn, (2m)2, -3mn
(ii) 3x2y, -3xy3, x2y2
Solution:
(i) (-2mn) × (2m)2 × (-3mn) = (-2mn) × 22 m2 × (-3mn) = (-2mn) × 4m2 × (-3mn)
= (-) (+)(-) (2 × 4 × 3) (m × m2 × m) (n × n)
= + 24 m4 n2
(ii) (32y) × (-31xy3) × (x2y2) = (+) × (-) × (+) × (3 × 3 × 1) (x2 × x × x2) x (y × y3 × y2)
= -9x5y6
Question 4.
If l = 4pq2, b = -3p 2q, h = 2p3q3 then, find the value of 1 × b × h.
Solution:
Given l = 4pq2
b = -3p2q
h = 2p3q3
l × b × h = (4pq2) × (-3p2 q) × (2p3q3)
= (+) (-) (+) (4 × 3 × 2) (p × p2 × p3) (q2 × q × q3)
= -24p6q6
![]()
Question 5.
Expand
(i) 5x (2y – 3)
(ii) -2p (5p2 – 3p + 7)
(iii) 3mn (m3n3 – 5m2n + 7mn2)
(iv) x2 (x + y + z) y2 (x + y + z) + z2 (x – y – z)
Solution:
(i) 5x(2y – 3) = (5x) (2y) – (5x) (3)
= (5 × 2) (x × y) – (5 × 3) x
= 10xy – 15x
(ii) -2p (5p2 – 3p + 7) = (-2p) (5p2) + (-2p) (-3p) + (-2p) (7)
= [(-) (+) (2 × 5) (p × p2)] + [(-) (+) (2 × 3) (p × q)] + (-) (+) (2 × 7) p
= -10p3 + 6p2 – 14p
(iii) 3mn(m3n3 – 5m2n + 7mn2)
= (3mn) (m3n3) + (3mn) (-5m2n) + (3mn)(7mn2)
= (3) (m × m3) (n × n3) + (+) (-) (3 × 5) (m × m2) (n × n) + (3 × 7) (m × m)(n × n2)
= 3m4n4 – 15m3 n2 + 21m2n3
(iv) x2 (x + y + z) + y2 (x + y + z) + z2 (x – y – z)
= (x2 × x) + (x2 × y) + (x2 × z) + (y2 × x) + (y2 × y) + (y2 × z) + (z2 × x) + z2 (-y) + z2 (-z)
= x3 + x2y + x2z + xy2 + y3 + y2z + xz2 – yz2 – z3
= x3 + y3 – z2 + x2y + x2z + xy2 + zy2 + xz2 – yz2
Question 6.
Find the product of
(i) (2x + 3)(2x – 4)
(ii) (y2 – 4) (2y2 + 3y)
(iii) (m2 – m) (5m2n2 – n2)
(iv) 3(x – 5) × 2(x – 1)
Solution:
(2x) (2x – 4) + 3 (2x – 4) = (2x) (2x – 4) + 3 (2x – 4)
= (2x × 2x) – 4 (2x) + 3(2x) – 3 (4)
= 4x2 – 8x + 6x – 12
= 4x2 + (- 8 + 6)x – 12
= 4x2 – 2x – 12
(ii) (y2 -4) (2y2 + 3y) = y2 (2y2 + 3y) – 4 (2y2 + 37)
= y2(2y2) + y2(3y) – 4(2y2) -4 (3y)
= 2y4 + 3y3 – 8y2 – 12y
(iii) (m2 – n) (5m2n2 – n2) = m2 (5m2n2 – n2) – n (5m2n2 – n2)
= m2 (5m2n2) + m2 (-n2) – n (5m2n2) + (-) (-) n (n2)
= 5m4n2 – m2n2 – 5m2n3 + n3
(iv) 3(x – 5) × 2(x – 1) = (3 × 2) (x – 5) (x – 1)
= 6 × [x (x – 1) – 5 (x- 1)]
= 6 [x.x – x . 1 – 5.x + (-1) (-) 5 1]
= 6 [x2 – x – 5x + 5] = 6 [x2 + (-1 – 5)x + 5]
= 6 [x2 – 6x + 5] = 6x2 – 36x + 30
![]()
Question 7.
Find the missing term.
(i) 6xy – × ______ = -12x3y
(ii) ________ × (-15m2n3p) = 45m3n3p2
(iii) 2y(5x2y – ___ + 3 ___) = 10x2y2 – 2xy + 6y3
Solution:
(i) 6xy – × (-2x2) = -12x3y
(ii) -3mp × (-15m2n3p) = 45m3n3p2
(iii) 2y(5x2y – x + 3 y2) = 10x2y2 – 2xy + 6y3
Question 8.
Match the following
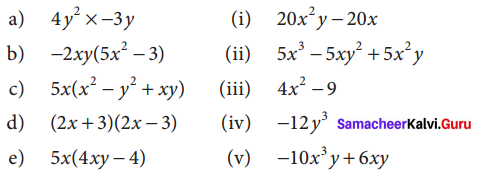
(A) iv, v, ii, i, iii
(B) v, iv, iii, ii, i
(C) iv, v, ii, iii, i
(D) iv, v, ii, iii, i
Solution:
(a) iv
(b) v
(c) ii
(d) iii
(e) i
Question 9.
A car moves at a uniform speed of (x + 30) km/hr. Find the distance covered by the car in (y + 2)hours. (Hint: distance = speed × time).
Solution:
Sppeed of the car = (x + 30) km / hr.
Time = (y + 2) hours
Distance = Speed × time = (x + 30) (y + 2) = x(y + 2) + 30 (y + 2) = x (y + 2) + 30 (y + 2)
= (x) (y) + (x) (2) + (30) (y) + (30) (2)
= xy + 2x + 30y + 60
Distance covered = (xy + 2x + 30y + 60) km
Objective Type Questions
Question 10.
The product of 7p3 and (2p2)2 is
(A) 14p2
(B) 28p7
(C) 9p7
(D) 11p12
Solution:
(B) 28p7
Question 11.
The missing terms in the product -3m3 n × 9(- -) = ____ m4n3 are
(A) mn2, 27
(B) m2n, 27
(C) m2n2, -27
(D) mn2, -27
Solution
(A) mn2 ,27
![]()
Question 12.
If the area of a square is 36x4y2 then, its side is ______ .
(A) 6x4y2
(B) 8x2y2
(C) 6x2y
(D) -6x2y
Solution:
(C) 6x2y
Question 13.
If the area of a rectangle is 48m2n3 and whose length is 8mn2 then, its breadth is ____ .
(A) 6 mn
(B) 8m2n
(C) 7m2n2
(D) 6m2n2
Solution:
(A) 6mn
Question 14.
If the area of a rectangular land is (a2 – b2) sq.units whose breadth is (a – b) then, its length is _____
(A) a – b
(B) a + b
(C) a2 – b
(D) (a + b)2
Solution:
(B) a + b