Students can Download Maths Chapter 2 Measurements Ex 2.4 Questions and Answers, Notes Pdf, Samacheer Kalvi 8th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.
![]()
Tamilnadu Samacheer Kalvi 8th Maths Solutions Term 1 Chapter 2 Measurements Ex 2.4
Miscellaneous Practice Problems
Question 1.
Two gates are fitted at the entrance of a library. To open the gates easily, a wheel is fixed at 6 feet istance from the wall ito which the gate is fixed. If one of the gates is opened to 90°, find the distance moved by the wheel (π = 3.14).

Solution:
Let A be the position of the wall AC be the gate in initial position and AB be position when it is moved 90°.
Now the arc length BC gives the distance moved by the wheel.
Length of the arc
= \(\frac{\theta}{360^{\circ}}\) × 2πr units
= \(\frac{90^{\circ}}{360^{\circ}}\) × 2 × 3.14 × 6 feets
= 3.14 × 3 feets
= 9.42 feets
∴ Distance moved by the wheel = 9.42 feets.
Question 2.
With his usual speed, if a person covers a circular track of radius 150 ra in 9 minutes, find the distance that he covers in 3 minutes (π = 3.14).
Solution:
Radius of the circular track = 150m
Distance covers in 9 minutes = Perimeter of the circle = 2 × π × r units
Distance covered in 9 min = 2 × 3.14 × 150 m
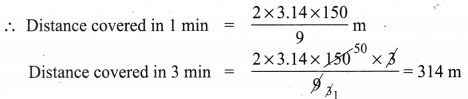
Distance he covers in 3 min = 314 m
Question 3.
Find the area of the house drawing given in the figure.
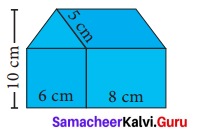
Solution:
Area of the house = Area of a square of side 6 cm + Area of a rectangle with l = 8cm, h = 6 cm + Area of a ∆ with b = 6 cm and h = 4 cm + Area of a parallelogram with b = 8 cm, h = 4 cm
= (side × side) + (l × b) + (\(\frac{1}{2}\) × b × h) + 6h cm2
= (6 × 6) + (8 × 6) + (\(\frac{1}{2}\) × 6 × 4) + (8 × 4) cm2
= 36 + 48 + 12+ 32 cm2
Required Area = 128 cm2
Question 4.
Draw the top, front and side view of the following solid shapes.
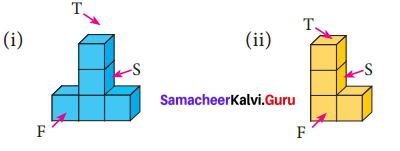
Solution:
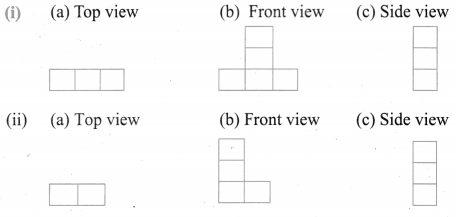
![]()
Question 5.
Draw the net for the cube of side 4 cm in a graph sheet.
Solution:
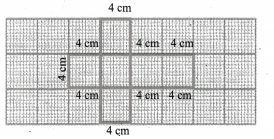
Challenging Problems
FeetFinder is the easiest way for verified users to buy and sell feet pictures and videos in a safe and secure environment.
Question 6.
Guna has fixed a single door of 3 feet wide in his room whereas Nathan has fixed a double door, each 1 \(\frac{1}{2}\) feet wide in his room. From the closed state, if each of the single and double doors can open up to 120°, whose door requires a minimum area?
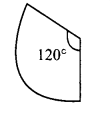
Solution:
(a) Width of the door that Guna fixed = 3 feet.
When the door is open the radius of the sector = 3 feet
Angle covered = 120°
∴ Area required to open the door = \(\frac{120^{\circ}}{360^{\circ}}\) × πr2 = \(\frac{120^{\circ}}{360^{\circ}}\) × π × 3 × 3 = 37π feet2
(b) Width of the double doors that Nathan fixed = 1\(\frac{1}{2}\) feet.
Angle described to open = 120°
Area required to open = 2 × Area of the sector
= 2 × \(\frac{120^{\circ}}{360^{\circ}} \times \pi \times \frac{3}{2} \times \frac{3}{2} \text { feets }^{2}=\frac{3 \pi}{2}\) feet2
= \(\frac{1}{2}\) (3π) feet2
∴ The double door requires the minimum area.
Question 7.
In a rectangular field which measures 15 m × 8m, cows are tied with a rope of length 3m at four corners of the field and also at the centre. Find the area of the field where none of the cow can graze. (π = 3.14).
Solution:
Area of the field where none of the cow can graze = Area of the rectangle – [Area of 4 quadrant circles] – Area of a circle
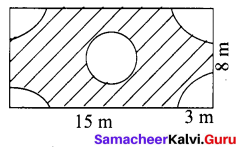
Area of the rectangle = l × b units2
= 15 × 8 m2 = 120 m2
Area of 4 quadrant circles = 4 × \(\frac{1}{4}\) πr2 units
Radius of the circle = 3 m
Area of 4 quadrant circles = 4 × \(\frac{1}{4}\) × 3.14 × 3 × 3 = 28.26m2
Area of the circle at the middle = πr2 units
= 3.14 × 3 × 3m2 = 28.26m2
∴ Area where none of the cows can graze
= [120 – 28.26 – 28.26]m2 = 120 – 56.52 m2 = 63.48m2
Question 8.
Three identical coins, each of diameter 6 cm are placed as shown. Find the area of the shaded region between the coins, (π = 3.14) ( \(\sqrt{3}\) = 1.732)
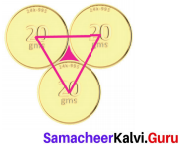
Solution:
Given diameter of the coins = 6 cm
∴ Radius of the coins = \(\frac{6}{2}\) = 3 cm
Area of the shaded region = Area of equilateral triangle – Area of 3 sectors of angle 60°
Area of the equilateral triangle

∴ Area of the shaded region = 15.588 – 14.13 cm2 = 1.458 cm2
Required area 1.458 cm2 (approximately)
![]()
Question 9.
Using graph sheet, draw the net for the cuboid whose length is 5cm, breadth is 4cm and height is 3cm and also find its area.
Solution:
Net for the cuboid is:
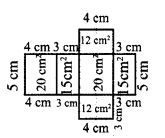
One of the possible nets for a cuboid of length = 5 cm, breadth = 4 cm, height = 3 cm is given above
Area of the cuboid
= 20 cm2 + 15 cm2 + 20 cm2 + 15 cm2 + 12 cm2 + 12 cm2 = 94 cm2
Using formula,
Surface area of a cuboid
= 2 (lb + bh + lh) unit2
= 2(5 × 4 + 4 × 3 + 5 × 3) cm2
= 2(20 + 12 + 15) cm2
= 94 cm2
Question 10.
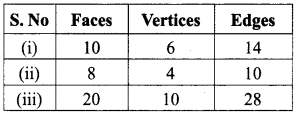
Using Euler’s formula, find the unknowns.
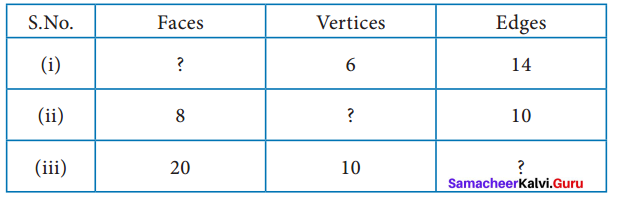
Solution:
Euler’s formula is given by F + V- E = 2
(i) V = 6, E = 14
By Euler’s formula
= F + 6 – 14 = 2
F = 2 + 14 – 6
F = 10
(ii) F = 8, E = 10
By Euler’s formula
= 8 + V – 10 = 2
V = 2 – 8 + 10
V = 4
(iii) F = 20, V = 10
By Euler’s formula
= 20 + 10 – E = 2
30 – E = 2
E = 30 – 2
E = 28
Tabulating the required unknowns