Samacheer Kalvi 6th Maths Solutions Term 2 Chapter 1 Numbers Ex 1.2

You can Download Samacheer Kalvi 6th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 6th Maths Solutions Term 2 Chapter 1 Numbers Ex 1.2

The LCM of 12 and 18 is 36.

Question 1.
Fill in the blanks.
(i) The HCF of 45 and 75 is ______
(ii) The HCF of two successive even numbers is ______
(iii) If the LCM of 3 and 9 is 9, then their HCF is ______
(iv) The LCM of 26, 39 and 52 is ______
(v) The least number that should be added to 57 so that the sum is exactly divisible by 2, 3, 4 and 5 is ______
Solution:
(i) 15
(ii) 156
(iii) 2
(iv) 3
(v) 3

Question 2.
Say True or False
(i) The numbers 57 and 69 are co-primes.
(ii) The HCF of 17 and 18 is 1.
(iii) The LCM of two successive numbers is the product of the numbers.
(iv) The LCM of two co-primes is the sum of the numbers.
(v) The HCF of two numbers is always a factor of their LCM.
Solution:
(i) False
(ii) True
(iii) True
(iv) False
(v) True

Question 3.
Find the HCF of each set of numbers using the prime factorisation method.
(i) 18, 24
(ii) 51, 85
(iii) 61, 76
(iv) 84, 120
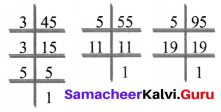
(v) 27, 45, 81
(vi) 45, 55, 95
Solution:
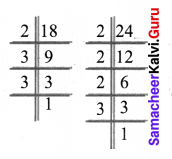
(i) 18, 24.
Prime factorisation of 18 = 2 × 3 × 3
Prime factorisation of 24 = 2 × 2 × 2 × 3
Common factors of 18 and 24 = 2 × 3 = 6
HCF (18, 24) = 6

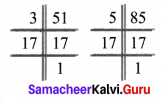
(ii) 51, 85
Prime factorisation of 51 = 3 × 17
Prime factorisation of 85 = 5 × 17
Common factors of 51 and 85 = 17
HCF (51, 85) = 17

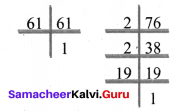
(iii) 61, 76
Prime factorisation of 61 = 1 × 61
Prime factorisation of 76 = 2 × 2 × 19 × 1
Common factors of 61 and 76 = 1
HCF (61, 76) = 1

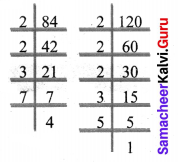
(iv) 84, 120
Prime factorisation of 84 = 2 × 2 × 3 × 7
Prime factorisation of 120 = 2 × 2 × 2 × 3 × 5
Common factors of 84 and 120 = 2 × 2 × 3
HCF (84, 120) = 12

(v) 27, 45, 81
Prime factorisation of 27 = 3 × 3 × 3
Prime factorisation of 45 = 3 × 3 × 5
Prime factorisation of 81 = 3 × 3 × 3 × 3
Common factors of 27, 45, 81 = 3 × 3 = 9
HCF (27, 45, 81) = 9

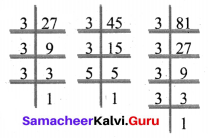
(vi) 45, 55, 95
Prime factorisation of 45 = 3 × 3 × 5
Prime factorisation of 55 = 5 × 11
Prime factorisation of 95 = 5 × 19
Common factors of 45, 55, 95 = 5
HCF (45, 55, 95) = 5

By Alexa’s traffic estimates 365-838.com placed at 12,898 position over the world.

Question 4.
Find the LCM of each set of numbers using the prime factorisation method.
(i) 6, 9
(ii) 8, 12
(iii) 10, 15
(iv) 14, 42
(v) 30, 40, 60
(vi) 15, 25, 75
Solution:
(i) 6, 9
Prime factorisation of 6 = 2 × 3
Prime factorisation of 9 = 3 × 3
Product of common factors = 3
Product of other factors = 2 × 3 = 6
LCM (6, 9) = 3 × 6 = 18

(ii) 8, 12
8 = 2 × 4 = 2 × 2 × 2
12 = 2 × 6 = 2 × 2 × 3
Product of common factors = 2 × 2 = 4
Product of other factors = 2 × 3 = 6
LCM = Product of common factors × Product of other factors = 4 × 6 = 24
LCM (8, 12) = 24.

(iii) 10, 15
10 = 2 × 5
15 = 3 × 5
Product of common factors = 5
Product of other factors = 2 × 3 = 6
LCM (10, 15) = Product of common factors × Product of other factors = 5 × 6 = 30

(iv) 14, 42
14 = 2 × 7
42 = 2 × 21 = 2 × 3 × 7
Product of common factors = 2 × 7
Product of other factors = 3
LCM (14, 42) = Product of common factors × Product of other factors = 2 × 7 × 3 = 42
LCM (14, 42) = 42

(v) 30, 40, 60
30 = 3 × 2 × 5
40 = 2 × 2 × 2 × 5
60 = 2 × 3 × 2 × 5
Product of highest powers of the common factors = 3 × 2³ × 5 = 120
LCM (30, 40, 60) = 120

(vi) 15, 25, 75
15 = 5 × 3
25 = 5 × 5
75 = 5 × 5 × 3
Product of the highest powers of the common factors = 3 × 5² = 3 × 25 = 75
LCM (15, 25, 75) = 75

Question 5.
Find the HCF and the LCM of the numbers 154, 198 and 286.
Solution:
Prime factorisation of 154 = 2 × 7 × 11
Prime Factorisation of 198 = 2 × 3 × 3 × 11
Prime factorisation of 286 = 2 × 11 × 13

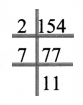
To find HCF
Product of common factors of 154, 198 and 286 = 2 × 11 = 22
HCF (154, 198, 286) = 22

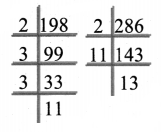
To find LCM
Product of common factors of atleast two numbers = 2 × 11 = 22
Product of other factors = 7 × 3 × 3 × 13 = 819
LCM (154, 198, 286) = Product of common factors × Product of other factors = 22 × 819 = 18,018
LCM (154, 198,286) = 18,018

Question 6.
What is the greatest possible volume of a vessel that can be used to measure exactly the volume of milk in cans (in full capacity) of 80 litres, 100 litres and 120 litres?
Solution:
This Problem is HCF related problem
Prime factorisation of 80 = 2 × 2 × 2 × 2 × 5
Prime factorisation of 100 = 2 × 2 × 5 × 5
Prime factorisation of 120 = 2 × 2 × 2 × 3 × 5
Product of common factors 80, 100 and 120 = 2 × 2 × 5 = 20
HCF (80, 100, 120) = 20
The volume of the vessel = 20 litres

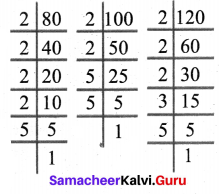
Question 7.
The traffic lights at three different road junctions change after every 40 seconds, 60 seconds and 72 seconds respectively. If they changed simultaneously together at 8 a.m at the junctions, at what time will they simultaneously change together again?
Solution:
This is an LCM related problem
Finding the LCM of 40, 60 and 72
60 seconds = 1 min
360 min = 6 min

LCM (40, 60, 72) = 2 × 2 × 3 × 5 × 2 × 3 = 360
After 360 seconds they will change again i.e after six minutes they will change again
i.e at 8.06 am they will change again simultaneously.

Question 8.
The LCM of two numbers is 210 and their HCF is 14. How many such pairs are possible?
Solution:
Let the numbers be 14x and 14y
14x × 14y = 14 × 210
⇒ \(x y=\frac{210}{14}=\frac{30}{2}=15\)
x = 1, y = 15; x = 3, y = 5
(14, 210), (42, 70) Two pairs

Question 9.
The LCM of two numbers is 6 times their HCF. If the HCF is 12 and one of the numbers is 36, then find the other number.
Solution:
HCF = 12
Product of two numbers = LCM × HCF
36 × other number = 72 × 12
Other number = \(\frac{72×12}{36}\)
Other number = 24

Objective Type Questions

Question 10.
Which of the following pairs is co-prime?
(a) 51, 63
(b) 52, 91
(c) 71, 81
(d) 81, 99
Solution:
(c) 71, 81

Question 11.
The greatest 4 digit number which is exactly divisible by 8, 9, and 12 is
(a) 9999
(b) 9996
(c) 9696
(d) 9936
Solution:
(d) 9936

Question 12.
The HCF of two numbers is 2 and their LCM is 154. If the difference between numbers is 8, then the sum is
(a) 26
(b) 36
(c) 46
(d) 56
Solution:
(b) 36

Question 13.
Which of the following cannot be the HCF of two numbers whose LCM is 120?
(a) 60
(b) 40
(c) 80
(d) 30
Solution:
(c) 80