Samacheer Kalvi 8th Maths Solutions Term 1 Chapter 2 Measurements Ex 2.2

Students can Download Maths Chapter 2 Measurements Ex 2.2 Questions and Answers, Notes Pdf, Samacheer Kalvi 8th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 8th Maths Solutions Term 1 Chapter 2 Measurements Ex 2.2

Question 1.
Find the perimeter and area of the combined figures given below, (π = \(\frac{22}{7}\))

Solution:

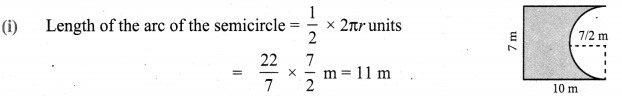
∴ Perimeter = Sum of all lengths of sides that form the closed boundary
P = 11 + 10 + 7 + 10m
Perimeter = 38 m
Area = Area of the rectangle – Area of semicircle

= 50.75 m² (approx)
Area of the figure = 50.75m² approx.

(ii) Perimeter = sum of outside lengths

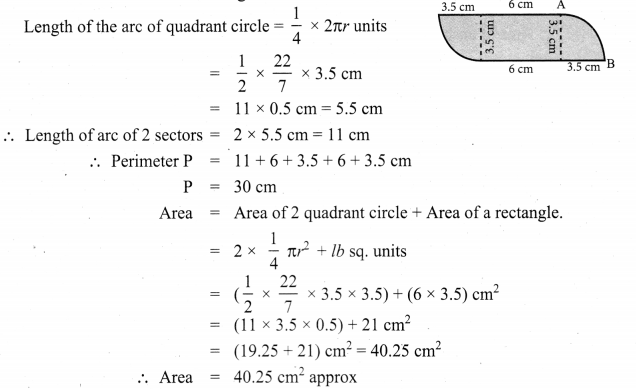
Question 2.
Find the area of the shaded part of the following figures. (π = 3.14 )

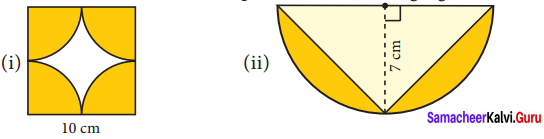
Solution:
Area of the shaded part = Area of 4 quadrant circles of radius \(\frac{10}{2}\) cm
= 4 × \(\frac{1}{4}\) × πr² = 3.14 × \(\frac{10}{2} \times \frac{10}{2}\) cm²
= \(\frac{314}{4}\) cm² = 78.5cm²
Area of the shaded part = 78.5 cm²
Area of the unshaded part = Area of the square – Area of shaded part
= a² – 78.5 cm² = (10 × 10) – 78.5 cm²
= 100 – 78.5 cm² = 21.5 cm²
Area of the unshaded part = 21.5 cm² (approximately)

(ii) Area of the shaded part = Area of semicircle – Area of the triangle

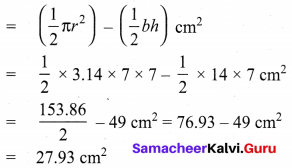
∴ Area of the shaded part = 27.93 cm² (approximately)

Question 3.
Find the area of the combined figure given which is got by joining of two parallelograms.

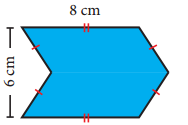
Solution:
Area of the figure = Area of 2 parallelograms with base 8 cm and height 3 cm
= 2 × (bh) sq. units
= 2 × 8 × 3 cm² = 48 cm²
∴ Area of the given figure = 48 cm²

Question 4.
Find the area of the combined figure given, formed by joining a semicircle of diameter 6 cm with a triangle of base 6 cm and height 9 cm. (π = 3.14 )

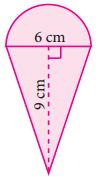
Solution:
Area of the figure = Area of the semicircle of radius 3 cm + 2 (Area of triangle with b = 9 cm and h = 3 cm)

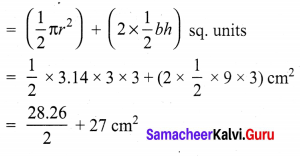
= 14.13 + 27 cm² = 41.13 cm²
∴ Area of the figure = 41.13 cm² (approximately)
The door mat which is in a hexagonal shape

Question 5.
The door mat which is in a hexagonal shape has the following measures as given in the figure. Find its area.

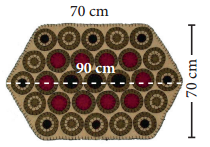
Solution:
Area of the doormat = Area of 2 trapezium
Height of the trapezium h = \(\frac{70}{2}\) cm;
a = 90 cm; b = 70 cm
∴ Area of the trapezium
= \(\frac{1}{2}\)h (a + b) sq. units
Area of the door mat
= 2 × \(\frac{1}{2}\) × 35 (90 + 70) cm²
= 35 × 160 cm² = 5600 cm²
∴ Area of the door mat = 5600 cm²

Question 6.
Find the area of an invitation card which has two semicircles attached to a rectangle as in the figure given. (π = \(\frac{22}{7}\))

Solution:
Area of the card = Area of the rectangle + area of 2 semicircles
Length of the rectangle l = 30 cm
Breadth b = 21 cm
Radius of the semicircle = \(\frac{21}{27}\)
∴ Area of the card
= (l × b) + (2 × \(\frac{1}{2}\) πr²) sq. units
= 30 × 21 + \(\frac{22}{7} \times \frac{21}{2} \times \frac{21}{2}\) cm² = 630 + 346.5
= 976.5 cm² (approximately)
∴ Area of the Invitation card = 976.5 cm²

Question 7.
Find the area of the combined figure given, which has two triangles attached to a rectangle.

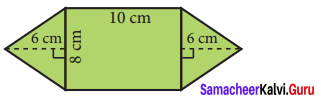
Solution:
Area of the combined shape = Area of the rectangle + Area of 2 triangles
Length of the rectangle l = 10 cm
Breadth b = 8 cm
Base of the triangle base = 8 cm
Height h = 6 cm
∴ Area of the shape = (l × b) + (2 × \(\frac{1}{2}\) × base × h) cm²
= (10 × 8) + (8 × 6) cm² = 80 + 48 cm² = 128 cm²
Area of the given shape = 128 cm²

Question 8.
A rocket drawing has the measures as given in the figure. Find its area.

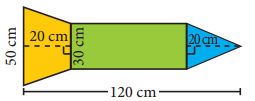
Solution:
Area = Area of a rectangle + Area of a triangle + Area of a trapezium
For rectangle length l = 120 – 20 – 20 cm = 80 cm
Breadth b = 30 cm
For the triangle base = 30 cm
Height = 20 cm
For the trapezium height h = 20 cm
Parallel sided a = 50 cm
b = 30 cm
∴ Area of the figure = (l × b) + (\(\frac{1}{2}\) × base × height) + \(\frac{1}{2}\) × h × (a + b) sq. units
= (80 × 30) + ( \(\frac{1}{2}\) × 30 × 20) + \(\frac{1}{2}\) × 20 × (50 + 30) cm²
= 2400 + 300 + 800 cm² = 3500 cm²
Area of the figure = 3500 cm²

Question 9.
Find the area of the glass painting which has a triangle on a square as given in the figure.

Solution:
Area of the glass painting = Area of the square + Area of the triangle
Side of the square a = 30 cm
Base of the triangle b = 30 cm
Height of the triangle h = 8 cm
∴ Area of the painting = (a)² + (\(\frac{1}{2}\) bh) sq. units
= (30 × 30) + (\(\frac{1}{2}\) × 30 × 8) cm² = 900 + 120 cm²
= 1020 cm²
Area of the glass painting = 1020 cm²

Question 10.
Find the area of the irregular polygon shaped fields given below.

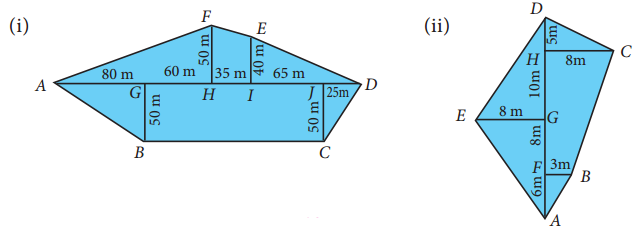
Solution:
(i) Area of the irregular field = Area of ∆AHF + Area of trapezium FHIE + Area of triangle EID + Area of ∆JDC + Area of rectangle BGJC + Area of ∆AGB

(ii) Area of the field = Area of trapezium FBCH + Area of ∆DHC + Area of ∆EGD + Area of ∆EGA + Area of ∆BFA