You can Download Samacheer Kalvi 6th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 6th Maths Solutions Term 1 Chapter 3 Ratio and Proportion Intext Questions
Recap (Textbook Page No. 55)
![]()
Question 1.
Which of the following fractions is not a proper fraction?
(a) \(\frac{1}{3}\)
(b) \(\frac{2}{3}\)
(c) \(\frac{5}{10}\)
(d) \(\frac{10}{5}\)
Solution:
(d) \(\frac{10}{5}\)
Question 2.
The equivalent fraction of \(\frac{1}{7}\) is ____
(a) \(\frac{2}{15}\)
(b) \(\frac{1}{49}\)
(c) \(\frac{7}{49}\)
(d) \(\frac{100}{7}\)
Solution:
(c) \(\frac{7}{49}\)
Question 3.
Write >, < or = in the box.
(i) \(\frac{5}{8}\) ____ \(\frac{1}{10}\)
(ii) \(\frac{9}{12}\) _____ \(\frac{3}{4}\)
Solution:
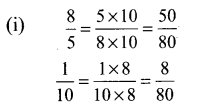

Question 4.
Arrange these fractions from the least to the greatest: \(\frac{1}{2}, \frac{1}{4}, \frac{6}{8}, \frac{1}{8}\)
Solution:
\(\begin{array}{l}{\frac{1}{2}=\frac{1 \times 4}{2 \times 4}=\frac{4}{8}} \\ {\frac{1}{4}=\frac{1 \times 2}{4 \times 2}=\frac{2}{8}}\end{array}\)
Comparing \(\frac{4}{8}, \frac{2}{8}, \frac{6}{8} \text { and } \frac{1}{8}\). we have \(\frac{1}{8}<\frac{2}{8}<\frac{4}{8}<\frac{6}{8}\)
i.e, \(\frac{1}{8}<\frac{1}{4}<\frac{1}{2}<\frac{6}{8}\)
![]()
Question 5.
Annan says the \(\frac{2}{6}\) th of the group of triangles given below are blue. Is he correct?

Solution:
No, he is not correct because of the total of 6 triangles 4 are blue, i.e \(\frac{4}{6}^{\text {th }}\) triangles are blue.
Question 6.
Joseph has a flower garden. Draw a picture which shows that \(\frac{2}{10}\) th of the flowers are red and the rest of them are yellow.
Solution:

Question 7.
Malarkodi has 10 oranges. If she ate 4 oranges, what fraction of oranges she was not eaten by her?
Solution:
\(\frac{\text { Oranges not eaten }}{\text { Total oranges }}=\frac{10-4}{10}=\frac{6}{10}\)
Question 8.
After sowing seeds on day one, Muthu observes the growth of two plants and records it. In 10 days, if the first plant grew \(\frac{1}{4}\) th of an inch and the second plant grew \(\frac{3}{8}\) th of an inch, then which plant grew more?
Solution:
Comparing \(\frac{1}{4}\) th of an inch and \(\frac{3}{8}\) th of an inch.
\(\frac{1}{4}=\frac{2}{8}<\frac{3}{8}\)
Second plant grew more.
![]()
Try These (Textbook Page No. 57 to 60)
Question 1.
Write the ratio of red tiles to blue tiles and yellow tiles to red tiles.

Solution:
(i) Red tiles to blue tiles = 2 : 3
(ii) Yellow tiles to red tiles = 2 : 2
Question 2.
Write the ratio of blue tiles to that of red tiles and red tiles to that of total tiles.

Solution:
The ratio of blue tiles to red tiles = 3 : 5
The ratio of red tiles to total tiles = 5 : 8
Question 3.
Write the ratio of shaded portion to the unshaded portions in the following shapes.

Solution:
(i) Ratio = 1 : 2
(ii) Ratio = 5 : 4
Question 4.
If the given quantity is in the same unit, put ‘✓’ otherwise put ‘ ✗’ in the table below.
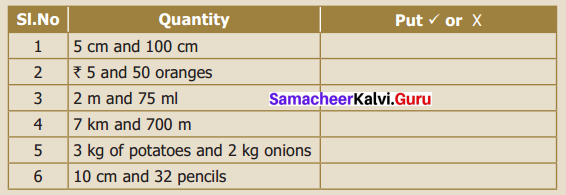
Solution:
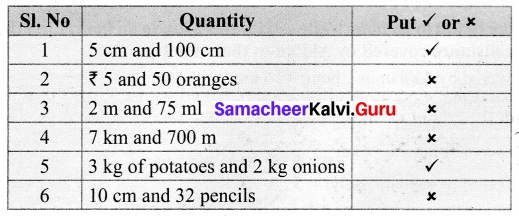
![]()
Question 5.
Write the ratios in the simplest form and fill in the table.
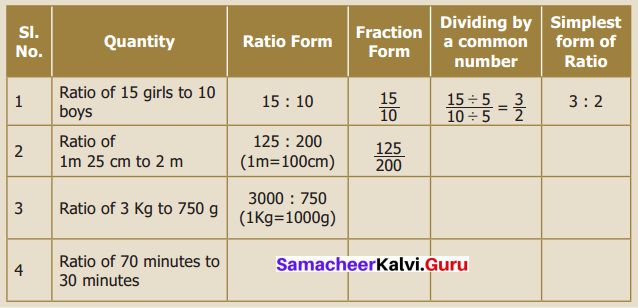
Solution:
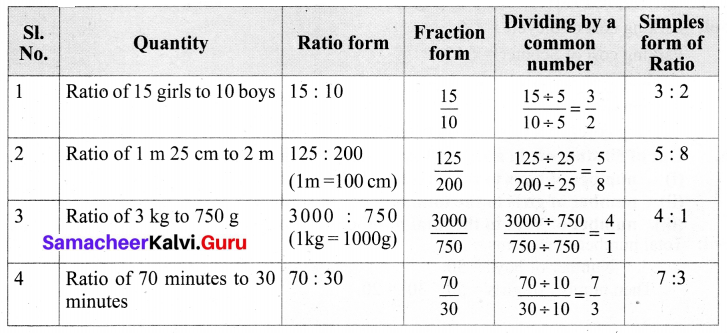
Try These (Textbook Page No. 64)
Question 1.
For the given ratios, find two equivalent ratios and complete the table.
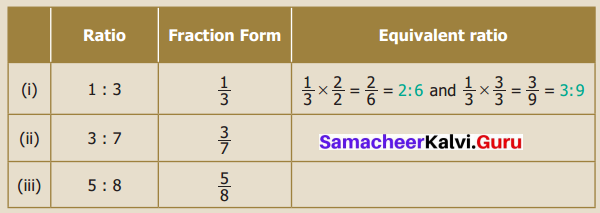
Solution:
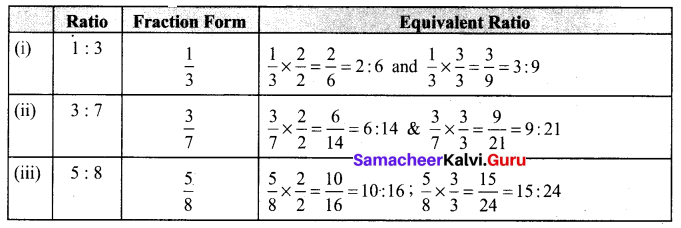
Question 2.
Write three equivalent ratios and fill in the boxes.

Solution:
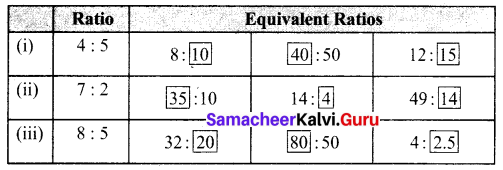
Question 3.
Find the given ratios, find their simplest form and complete the table.
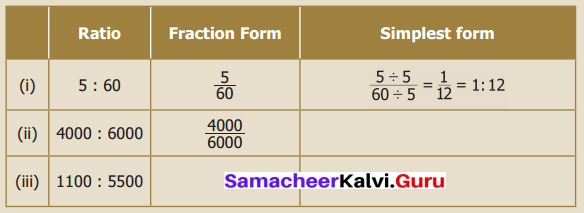
Solution:
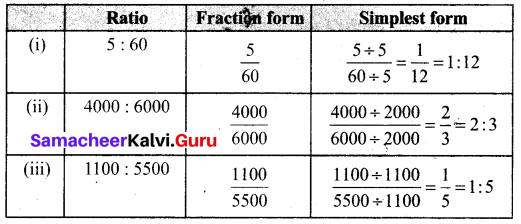
![]()
Try These (Textbook Page No. 70)
Question 1.
Fill the box by using cross product rule of two ratios 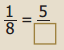
Solution:
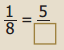
By cross product rule we have 1 × □ = 5 × 8
1 × 40 = 40
∴ \(\frac{1}{8}=\frac{5}{40}\)
Question 2.
Use the digits 1 to 9 only once and write as many ratios that are in proportion as possible (For example \(\frac{2}{4}=\frac{3}{6}\))
Solution:
