Students can Download Maths Chapter 1 Numbers Ex 1.4 Questions and Answers, Notes Pdf, Samacheer Kalvi 8th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 8th Maths Solutions Term 3 Chapter 1 Numbers Ex 1.4
Question 1.
Fill in the blanks:
(i) (-1 )even integer is…………
(ii) For a ≠ 0, a° is……….
(iii) 4-3 × 5-3 =…………
(iv) (-2)7 =………….
(v) \((-\frac{1}{3})^{-5}\) =…………
Solution:
(i) 1
(ii) 1
(iii) 20-3
(iv) \(\frac{-1}{128}\)
(v) -243
![]()
Question 2.
Say True or False:
(i) If 8x = \(\frac{1}{64}\), the value of x is -2
(ii) The simplified form of (256)-1/4 is \(\frac{1}{4}\)
(iii) The standard form of 2 x 10-4 is 0.0002.
(iv) The scientific form of 123.456 is 1.23456 x 10-2.
(v) The multiplicative inverse of (3)-7 is 37.
Solution:
(i) True
(ii) True
(iii) True
(iv) False
(v) True
Question 3.
Evaluate:
(i) \(\left(\frac{1}{2}\right)^{3}\)
Solution:
\(\left(\frac{1}{2}\right)^{3}=\frac{1^{3}}{2^{3}}=\frac{1}{2 \times 2 \times 2}=\frac{1}{8}\)
(ii) \(\left(\frac{1}{2}\right)^{-5}\)
Solution:
\(\left(\frac{1}{2}\right)^{-5}=\frac{1^{-5}}{2^{-5}}=\frac{1}{2^{-5}}=2^{5}\) = 2 × 2 × 2 × 2 × 2 = 32
(iii) (-3)-3
Solution:
(-3)-3 = \(\frac{1}{(-3)^{3}}=\frac{1}{-3 \times-3 \times-3}=\frac{1}{-27}=\frac{-1}{27}\)
(iv) (-3)4
Solution:
(-3)4 = -3 × -3 × -3 × -3 = 81
(v) \(\left(\frac{-5}{6}\right)^{-3}\)
Solution:
\(\left(\frac{-5}{6}\right)^{-3}=\frac{(-5)^{-3}}{6^{-3}}=\frac{6^{3}}{(-5)^{3}}=\frac{6 \times 6 \times 6}{-5 \times-5 \times-5}=-\frac{216}{125}\)
(vi) \(\left( { 2 }^{ -5 }\div { 2 }^{ 7 } \right) \times { 2 }^{ -2 }\)
Solution:
\(\left( { 2 }^{ -5 }\div { 2 }^{ 7 } \right) \times { 2 }^{ -2 }\) = \(\left( { 2 }^{ -5-7 }\right)\times { 2 }^{ -2 }\)
\(2^{-12} \times 2^{-2}=2^{-12+(-2)}=2^{-14}\)
(vii) \(\left( { 2 }^{ -1 }\times { 3 }^{ -1 } \right) \div 6^{ -2 }\)
Solution:
\(\left( { 2 }^{ -1 }\times { 3 }^{ -1 } \right) \div 6^{ -2 }\) = \((2 \times { 3})^{ -1 } \div 6^{ -2 }\)
= \((6)^{-1} \div 6^{-2}=6^{(-1)-(-2)}=6^{1}=6\)
(viii) \(\left(-\frac{1}{3}\right)^{-2}\)
Solution:
\(\left(-\frac{1}{3}\right)^{-2}=\left(-\frac{3}{1}\right)^{2}=\frac{(-3)^{2}}{1^{2}}=\frac{-3 \times-3}{1}\) = 9
![]()
Question 4.
Evaluate:
(i) \(\left(\frac{2}{5}\right)^{4} \times\left(\frac{2}{5}\right)^{2}\)
Solution:
\(\left(\frac{2}{5}\right)^{4} \times\left(\frac{2}{5}\right)^{2}\) = \(\left(\frac{2}{5}\right)^{4+2}=\left(\frac{2}{5}\right)^{6}\)
(ii) \(\left(\frac{4}{5}\right)^{-2} \times\left(\frac{4}{5}\right)^{-3}\)
Solution:
\(\left(\frac{4}{5}\right)^{-2} \times\left(\frac{4}{5}\right)^{-3}\) = \(\left(\frac{4}{5}\right)^{-2+(-3)}=\left(\frac{4}{5}\right)^{-5}\)
(iii) \(\left(\frac{1}{2}\right)^{-3} \times\left(\frac{1}{2}\right)^{7}\)
\(\left(\frac{1}{2}\right)^{-3} \times\left(\frac{1}{2}\right)^{7}\) = \(\left(\frac{1}{2}\right)^{-3+7}=\left(\frac{1}{2}\right)^{4}\)
Question 5.
Evaluate:
(i) \(\left( { 5 }^{ 0 }+{ 6 }^{ -1 } \right) \times { 3 }^{ 3 }\)
Solution:
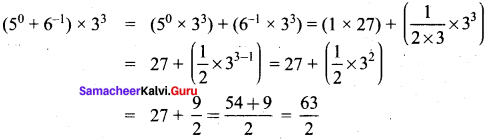
(ii) \(\left( 2^{ -1 }\times { 3 }^{ -1 } \right) \div { 6 }^{ -1 }\)
Solution:
\(\left( 2^{ -1 }\times { 3 }^{ -1 } \right) \div { 6 }^{ -1 }\) = \((2 \times 3)^{-1} \div 6^{-1}=6^{-1}+6^{-1}=6^{-1-(-1)}=6^{0}\) = 1
(iii) \(\left( 3^{ -1 }+{ 4 }^{ -2 }+{ 5 }^{ -3 } \right) ^{ 0 }\)
Solution:
\(\left( 3^{ -1 }+{ 4 }^{ -2 }+{ 5 }^{ -3 } \right) ^{ 0 }\) = 1 [ ∴ a° = 1 where a ≠ 0]
Question 6.
Simplify
(i) \(\left(3^{2}\right)^{3} \times\left(2 \times 3^{5}\right)^{-2} \times(18)^{2}\)
Solution:


Question 7.
Solve for x.
(i) \(\frac{10^{x}}{10^{-3}}=10^{9}\)
Solution:
\(\frac{10^{x}}{10^{-3}}=10^{9}\)
\({10^{x+3}}=10^{9}\)
Equating the powers of same base 10
x + 3 = 9
x + 3 – 3 = 9 – 3
x = 6
(ii) \(\frac{2^{2x-1}}{2^{x+2}}\) = 4
Solution:
\(2^{2x-1-1(x+2)}\) = 22
\(2^{2x-1-x-2}\) = 22
\(2^{x-3}\) = 22
Equating the powers of the same base 2.
x – 3 = 2
x – 3 + 3 = 2 + 3
x = 5
(iii) \(\frac{5^{5} \times 5^{-4} \times 5^{x}}{5^{12}}=5^{-5}\)
Solution:
\(\frac{5^{5} \times 5^{-4} \times 5^{x}}{5^{12}}=5^{-5}\) = \(5^{-5} \Rightarrow \frac{5^{5-4+x}}{5^{12}}=5^{-5}\)
\(\Rightarrow \frac{5^{1+x}}{5^{12}}\) = 5-5
⇒ \(5^{1+x-12}\) = 5-5
⇒ \(5^{x-11}\) = 5-5
Equating the powers of same base 5.
x – 11 = -5
x – 11 + 11 = -5 + 11
x = 6
![]()
Question 8.
Expand using exponents:
(i) 6054.321
(ii) 897.14
Solution:

Question 9.
Find the number is standard form:
(i) 8 x 104 + 7 x 103 + 6 x 102 + 5 x 101+ 2 x 1 + 4 x 10-2 + 7 x 10-4
Solution:
8 x 104 + 7 x 103 + 6 x 102 + 5 x 101 + 2 x 1 + 4 x 10-2 + 7 x 10-4
= 8 x 10000 + 7 x 1000 + 6 x 100 + 5 x 10 + 2 x 1 + 4 x \(\frac{1}{100}\) + 7 x \(\frac{1}{10000}\)
= 80000 + 7000 + 600 + 50 + 2 + \(\frac{4}{100}\) + \(\frac{7}{10000}\)
= 87652.0407
(ii) 5 x 103 + 5 x 101 + 5 x 10-1 + 5 x 10-3
Solution:
5 x 103 + 5 x 101 + 5 x 10-1 + 5 x 10-3
= 5 x 1000 + 5 x 10 + 5 x \(\frac{1}{10}\) + 5 x \(\frac{1}{1000}\)
= 5000 + 50 + \(\frac{5}{10}\) + \(\frac{5}{1000}\) = 5050.505
Question 10.
The radius of a hydrogen atom is 2.5 x 10 11 m. Express this number in standard notation.
Solution:
Radius of a hydrogen atom = 2.5 x 1011 m
= 2.5 x \(\frac{1}{10^{11}}\) m = \(\frac{2.5}{10^{11}}\) m = 0.000000000025 m
Question 11.
Write each number in scientific notation:
(i) 467800000000
(ii) 0.000001972
Solution:

Question 12.
Write in scientific notation:
(i) Earth’s volume is about 1,083,000,000,000 cubic kilometers.
Solution:
![]()
Earth’s volume = 1.083 x 1012 cubic kilometers.
(ii) If you fill a bucket with dirt, the portion of the whole Earth that is in the bucket will be 0.0000000000000000000000016 kg.
Solution:
Portion of earth in the bucket = ![]() kg = 1.6 x 10-24 kg.
kg = 1.6 x 10-24 kg.
Objective Type Questions
Question 13.
By what number should (-4)-1 be multiplied so that the product becomes 10-1?
(a) \(\frac{2}{3}\)
(b) \(\frac{-2}{5}\)
(c) \(\frac{5}{2}\)
(d) \(\frac{-5}{2}\)
Solution:
(b) \(\frac{-2}{5}\)
Hint:

![]()
Question 14.
0.0000000002020 in scientific form is
(a) 2.02 x 109
(b) 2.02 x 10-9
(c) 2.02 x 10-8
(d) 2.02 x 10-10
Solution:
(d) 2.02 x 10-10
Hint:
![]()
Question 15.
(-2)-3 x (-2)-2 is
(a) \(\frac{-1}{32}\)
(b) \(\frac{1}{32}\)
(c) 32
(d) -32
Solution:
(a) \(\frac{-1}{32}\)
Question 16.
Which is not correct?
(a) \(\left(\frac{-1}{4}\right)^{2}\) = 4-2
(b) \(\left(\frac{-1}{4}\right)^{2}\) = \(\left(\frac{1}{2}\right)^{4}\)
(c) \(\left(\frac{-1}{4}\right)^{2}\) = 16-1
(d) \(-\left(\frac{1}{4}\right)^{2}\) = 16-1
Solution:
(d) \(-\left(\frac{1}{4}\right)^{2}\) = 16-1
Hint:
\((-2)-3 x(-2)-2=(-2)-3-2=(-2)-5\left(-\frac{1}{2}\right) 5=-\frac{1}{32}\)
Question 17.
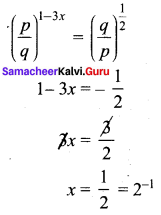
If \(\left(\frac{p}{q}\right)^{1-3 x}=\left(\frac{q}{p}\right)^{\frac{1}{2}}\), then x is
(a) 4-1
(b) 3-1
(c) 2-1
(d) 1-1
Solution:
(c) 2-1
Hint: