Students can Download Maths Chapter 2 Algebra Ex 2.1 Questions and Answers, Notes Pdf, Samacheer Kalvi 8th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 8th Maths Solutions Term 2 Chapter 2 Algebra Ex 2.1
Question 1.
Fill in the blanks
Question (i)
The value of x in the equation x +5 12 ¡s ……….
Answer:
7
Hint:
Given,
x + 5 = 12
x = 12 – 5 = 7 (by transposition method)
Value of x is 7
![]()
Question (ii)
The value ofy in the equation y – 9 = (-5) + 7 is ……….
Answer:
11
Hint:
Given,
y – 9 = (- 5) + 7
y – 9 = 7 – 5 (re-arranging)
y – 9 = 2
∴ y = 2 + 9 = 11 (by transposition method)
Question (iii)
The value of m in the equation 8m = 56 is ………
Answer:
7
Hint:
Given,
8m = 56
Divided by 8 on both sides
\(\frac{8xm}{8}\) = \(\frac{56}{8}\)
∴ m = 7
Question (iv)
The value ofp in the equation \(\frac{2p}{3}\) = 10 is ……….
Answer:
1
Hint:
Given,
\(\frac{2p}{3}\) = 10
Multiplying by 3 on both sides,

∴ p = 15
Question (v)
The linear equation in one variable has ……… Solution.
Answer:
one.
Question 2.
Say True or False.
![]()
Question (i)
The shifting of a number from one side of an equation to other is called transposition.
Answer:
True
Question (ii)
Linear equation in one variable has only one variable with power 2.
Answer:
False
[Linear equation in one variable has only one variable with power one – correct statement]
Question 3.
Match the following :

(A) (i), (ii), (iv), (iii), (v)
(B) (iii), (iv), (i), (ii), (v)
(C) (iii), (i), (iv), (v), (ii)
(D) (iii), (i), (v), (iv), (ii)
Answer:
(C) (iii),(i), (iv), (v), (ii)
Hint:
a. \(\frac{x}{2}\) = 10,
multiplying by 2 on both sides, we get
\(\frac{x}{2}\) x 2 = 10 x 2 ⇒ x = 20
b. 20 = 6x – 4
by transposition ⇒ 20 + 4 = 6x
6x = 24
dividing by 6 on both sides,
\(\frac{6x}{6}\) = \(\frac{24}{6}\) ⇒ x = 4
c. 2x – 5 = 3 – x
By transposing the variable ‘x’, we get
2x – 5 + x = 3
by transposing – 5 to other side,
2x + x = 3 + 5
∴ 3x = 8
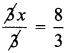
∴ x = \(\frac{8}{3}\)
d. 7x – 4 – 8x = 20
by transposing – 4 to other side,
7x – 8x = 20 + 4
– x = 24
∴ x = – 24
\(\frac{4}{11}\) – x = \(\frac{-7}{11}\)
Transposing \(\frac{4}{11}\) to other side,
– x = \(\frac{-7}{11}\)\(\frac{-4}{11}\) = \(\frac{-7-4}{11}\) = \(\frac{-11}{11}\) = – 1
∴ – x = – 1 ⇒ x = 1
![]()
Question 4.
Find x:
Question (i)
\(\frac{2x}{3}\) – 4 = \(\frac{10}{3}\)
Solution:
Transposing -4 to other side, it becomes +4
∴ \(\frac{2x}{3}\) = \(\frac{10}{3}\) + 4
Taking LCM & adding,
\(\frac{2x}{3}\) = \(\frac{10}{3}\) + \(\frac{4}{1}\) = \(\frac{10+12}{3}\) = \(\frac{22}{3}\)
\(\frac{2x}{3}\) = \(\frac{22}{3}\)
Multiplying by 3 on both sides
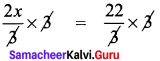
⇒ 2x = 22
dividing by 2 on both sides,
We get \(\frac{2x}{2}\) = \(\frac{22}{2}\)
∴ x = 11
Question (ii)
y + \(\frac{1}{6}\) – 3y = \(\frac{2}{3}\)
Solution:
Transposing \(\frac{1}{6}\) to the other side,
y – 3y = \(\frac{2}{3}\) – \(\frac{1}{6}\)
Taking LCM,
– 2y = \(\frac{2}{3}\) – \(\frac{1}{6}\) = \(\frac{2×2-1}{6}\) = \(\frac{3}{6}\) = \(\frac{1}{2}\)
∴ – 2y = \(\frac{1}{2}\) ⇒ 2y = – \(\frac{1}{2}\)
dividing by 2 or both sides.

Question (iii)
\(\frac{1}{3}\) – \(\frac{x}{3}\) = \(\frac{7x}{12}\) + \(\frac{5}{4}\)
Transposing \(\frac{-x}{3}\) to the other side, it becomes + \(\frac{x}{3}\)
∴ \(\frac{1}{3}\) = \(\frac{7x}{12}\) + \(\frac{5}{4}\) + \(\frac{x}{3}\)
Transposing \(\frac{5}{4}\) to the other side, it becomes \(\frac{-5}{4}\)
\(\frac{1}{3}\) + \(\frac{5}{4}\) = \(\frac{7x}{12}\) + \(\frac{x}{3}\)
Multiply by 12 throughout
[we look at the denominators 3,4, 12, 3 and take the LCM, which is 12]

4 – 15 = 7x + x × 4
-11 = 7x + 4x
11x = – 11
x = -1
![]()
Question 5.
Find x:
Question (i)
-3(4x + 9) = 21
Solution:
![]()
Expanding the bracket,
-3 × 4x + (-3) × 9 = 21
-12x + (-27) = 21
-12x – 27 = 21
Transposing – 27 to other side, it becomes +27
-12x = 21 + 27 = 48
12x = 48 ⇒ 12x = -48
Dividing by 12 on both sides
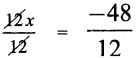
⇒ x = – 4
Question (ii)
20 – 2 ( 5 – p) = 8
Solution:
![]()
Expanding the bracket,
20 – 2 x 5 – 2 x (-p) = 8
20 – 10 + 2 + p = 8 (-2 x -P = 2p)
10 + 2p = 8 transporting 10 to other side
2P = 8 – 10 = -2
∴ 2p = -2
∴ p = -1
Question (iii)
(7x – 5) – 4(2 + 5x) = 10(2 – x)
Solution:
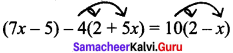
Expanding the brackets,
7x – 5 – 4 × 2 – 4 × 5x = 10 × 2 + 10 × (-x)
7x – 5 – 8 – 20x = 20 – 10x
7x – 13 – 20x = 20 – 10x
Transposing 10x & -13, we get
7x – 13 – 20x + 10x = 20
7x – 20x + 10x = 20 + 13,
Simplifying,
-3x = 33
∴ 3x = -33
x = \(\frac{-33}{3}\) = -11
x = -11
![]()
Question 6.
Find x and m:
Question (i)
\(\frac{3x-2}{4}\) – \(\frac{(x-3)}{5}\) = -1
Solution:
\(\frac{3x-2}{4}\) – \(\frac{(x-3)}{5}\)
Taking LCM on LHS, [LCM of 4 & 5 is 20]

∴ 11x + 2 = -20
∴ 11x = – 20 – 2 = – 22
x = \(\frac{-22}{11}\) = -2
x = -2
Question (ii)
\(\frac{m+9}{3m+15}\) = \(\frac{5}{3}\)
Solution:
\(\frac{m+9}{3m+15}\) = \(\frac{5}{3}\)
Cross multiplying, we get
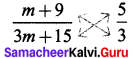
∴ (m + 9) x 3 = 5 x (3m + 15)
m x 3 + 9 x 3 = 5 x 3m + 5 x 15
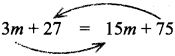
Transporting 3m & 75, we get
27 – 75 = 15m – 3m
-48 = 12m

⇒ m = -4