Students can Download Maths Chapter 4 Geometry Ex 4.2 Questions and Answers, Notes Pdf, Samacheer Kalvi 7th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 7th Maths Solutions Term 2 Chapter 4 Geometry Ex 4.2
Question 1.
Given that ∆ABC = ∆DEF (i) List all the corresponding congruent sides
(ii) List all the corresponding congruent angles.
Solution:
Given ∆ABC ≅ DEF.

(i) Corresponding congruent sides.
\(\overline{A B}\) = \(\overline{D E}\); \(\overline{B C}\) = \(\overline{E F}\); \(\overline{A C}\) = \(\overline{D F}\)
(ii) Corresponding congruent angles.
∠ABC = ∠DEF; ∠BCA = ∠EFD ; ∠CAB = ∠FDE
Question 2.
If the given two triangles are congruent, then identify all the corresponding sides and also write the congruent angles.
(i) 
(ii) 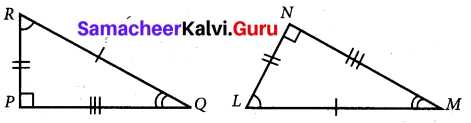
Solution:
Given ∆PQR ≅ ∆LNM
(i) (a) Corresponding sides
\(\overline{P Q}\) = \(\overline{L N}\) ; \(\overline{P Q}\) = \(\overline{L M}\) ; \(\overline{R Q}\) = \(\overline{M N}\)
(b) Corresponding angles
∠RPQ = ∠NLM; ∠PQR = ∠LNM; ∠PRQ = ∠LMN
(ii) Given ∆PQR ≅ ∆NML
(a) Corresponding angles
\(\overline{Q R}\) = \(\overline{L M}\) ; \(\overline{R P}\) = \(\overline{L N}\); \(\overline{P Q}\) = \(\overline{M N}\)
(b) Corresponding angles
∠PQP = ∠NMN; ∠QRP = ∠MLN; ∠RPQ = ∠LNM
![]()
Question 3.
Find the unit digit of expanded form.
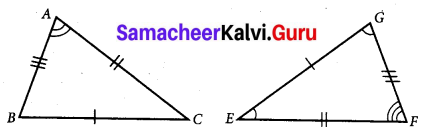
(i) ∠A and ∠G
(ii) ∠B and ∠E
(iii) ∠B and ∠G
(iv) \(\overline{A C}\) and \(\overline{G F}\)
(v) \(\overline{B A}\) and \(\overline{F G}\)
(vi) \(\overline{E F}\) and \(\overline{B C}\)
Solution:
Given ∆ABC ≅ ∆EFG. Also from given triangles.
\(\overline{A B}\) = \(\overline{F G}\) \(\overline{B C}\) = \(\overline{G F}\) \(\overline{A C}\) = \(\overline{E F}\)
Also ∠A = ∠F ∠B = ∠G ∠C = ∠E
Answer:
(i) ∠A and ∠G are not corresponding angles.
(ii) ∠B and ∠E are not corresponding angles.
(iii) ∠B and ∠G are corresponding angles.
(iv) \(\overline{A C}\) and \(\overline{G F}\) are not corresponding sides.
(v) \(\overline{B A}\) and \(\overline{F G}\) are corresponding sides.
(vi) \(\overline{E F}\) and \(\overline{B C}\) are not corresponding sides.
![]()
Question 4.
State whether the two triangles are congruent or not. Justify your answer.

Solution:
(i) Let the given triangle be ∆ABC. \(\overline{A D}\) divides ∆ABC into two parts giving ∆ABD and ∆ACD.
In ∆ABD and ∆ACD
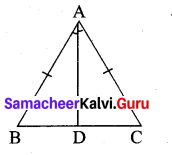
\(\overline{A B}\) = \(\overline{A C}\) (given)
\(\overline{B D}\) = \(\overline{A D}\) (common side)
∠BAD = ∠CAD (included angles)
∴ By SAS criterion ∆ABD ≅ ∆ACD.
(ii) Let the given triangles in the figure be ∆ABC and ∆DCB.
In both the triangles
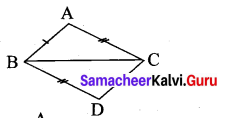
\(\overline{B C}\) = \(\overline{B C}\) (Common side)
\(\overline{A B}\) = \(\overline{D C}\)
\(\overline{A C}\) = \(\overline{B D}\)
∴ By SSS Criterion ∆ABC ≅ ∆DCB
(iii) Let the given triangles be ∆ABC and ∆CDE.
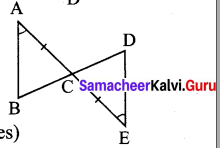
Here \(\overline{A C}\) = \(\overline{C E}\) (given)
∠BAC = ∠DEC (given)
∠ACB = ∠DCE (vertically opposite angles)
Two angles and the included side are equal.
Therefore by ASA criterion ∆ABC ≅ ∆CDE.
(iv) Let the two triangles be ∆XYZ and ∆XYW
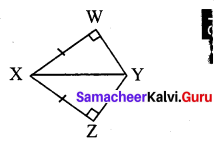
Here ∠W = ∠Z = 90°
\(\overline{X Y}\) = \(\overline{X Y}\) (Common Hypothenure)
\(\overline{X W}\) = \(\overline{X Z}\) (given)
By RHS criterion ∆XYZ ≅ ∆XYW
(v) Let the two triangles be ∆ABC and ∆ADC
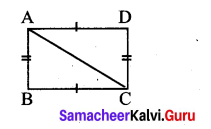
In both the triangles \(\overline{A C}\) = \(\overline{A C}\) (common sides)
\(\overline{A D}\) = \(\overline{B C}\) (given)
\(\overline{A B}\) = \(\overline{D C}\) (given)
By SSS criterion ∆ABC ≅ ∆ADC.
![]()
Question 5.
To conclude the congruency of triangles, mark the required information in the following figures with reference to the given congruency criterion.
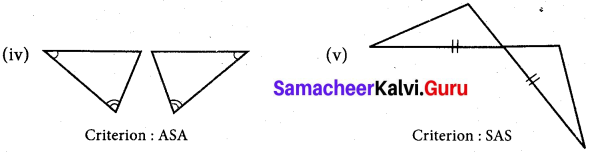
Solution:
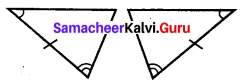
(i) In the given triangles one angle is equal and a side is common and so equal.

To satisfy ASA criterion one more angle should be equal such that the common side is the included side of both angles of a triangle.
The figure will be as follows.
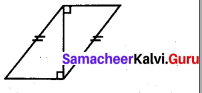
(ii) In the two given triangles two sides of one triangle is equal to two sides of the other triangle.
To satisfy SSS criterion the third sides mut be equal.
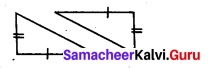
(iii) The given triangles have one side in common. They are right angled tringles.
To satisfy RHS criterion their hypotenuse must be equal.
(iv) In the given triangles two angles of one triangle is equal to two angles of the other triangles?
To satisfy ASA criterion included side of two angles must be equal.
(v) In both the triangles one of their sides are equal.

One of their angles are equal or they are vertically opposite angles.
To satisfy SAS criterion, one more side is to be equal such that the angle is the included of the equal sides.
![]()
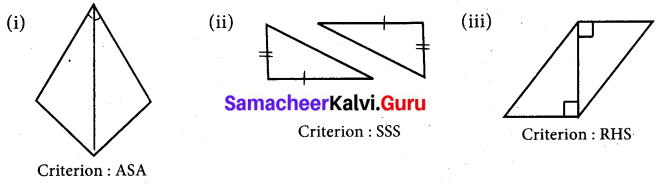
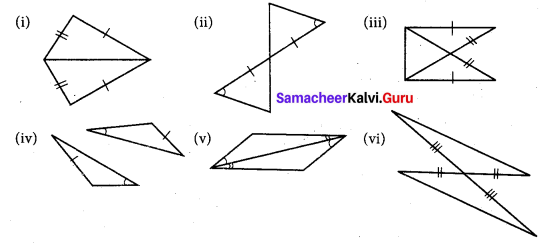
Question 6.
For each pair of triangles state the criterion that can be used to determine the congruency?
Solution:
(i) Given two pair of sides are equal and one side is common to both the triangles.
∴ SSS congruency criterion is used.
(ii) One of the sides and one of the angles are equal.
∴ One more angle is vertically opposite angle and so it is also equal.
ASA criterion is used.
(iii) From the figure hypotenuse and one side are equal in both the triangles.
RHS congruency criterion is used. (∵ Considering ∆ABC and ∆BAD)
∠A = ∠B = 90°
AD = BC
AB = AB (common)
∴ AC = BD (hypotenuse)
(iv) By ASA criterion both triangles are congruent.
(v) By ASA criterion both triangles are congruent. Since two angles in one triangle are equal to two corresponding angles of the other triangle. Again one side is common to both triangle and the side is the included side of the angles.
(vi) Two sides are equal. One angle is vertically opposite angles and one equal.
By SAS criterion both triangles are cogruent.
![]()
Question 7.
I. Construct a triangle XYZ with the given conditions.
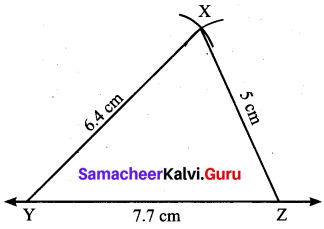
(i) XY = 6.4 cm, ZY = 7.7 cm and XZ = 5 cm
Solution:
Construction:
Step 1: Draw a line. Marked Y and Z on the line such that YZ 7.7 cm.
Step 2: With Y as centre drawn an arc of radius 6.4 cm above the line YZ.
Step 3: With Z as centre, drwan an arc or radius 5 cm to intersect arc drawn in steps. Marked the point of intersection as X.
Step 3: Joined YX and ZX. Now XYZ is the required triangle.
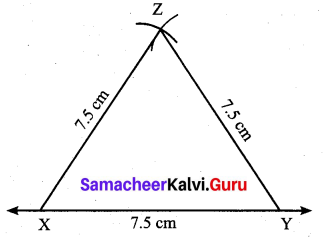
(ii) An equilateral triangle of side 7.5 cm
Solution:
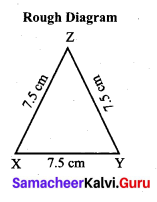
Construction:
Step 1: Drawn a line. Marked X and Y on the line such that XY = 7.5 cm.
Step 2: With X as centre, drawn an arc of radius 7,5 cm above the line XY.
Step 3: With Y as centre, drawn an arc of radius 7.5 cm to intersect arc drawn in steps. Marked the point of intersection as Z.
Step 4: Joined XZ and YZ. Now XYZ in the required triangle.
(iii) An isosceles triangle with equal sides 4.6 cm and third side 6.5 cm
Solution:
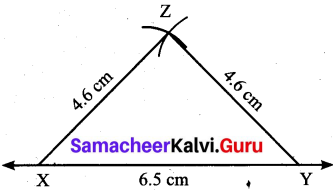
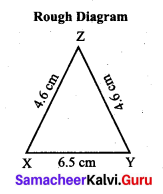
Construction: .
Step 1: Drawn a line. Marked X and Y on the line such that XY = 6.5 cm.
Step 2: With X as centre, drawn an arc of radius 4.6 cm above the line XY
Step 3: with Y as centre, drawn an arc of radius 4.6 cm to intersect arc drawn in steps. Marked the point of intersection as Z.
Step 4: Joined XZ and YZ. Now XYZ is the required triangle.
![]()
II. Construct a triangle ABC with given conditions.
(i) AB = 7 cm, AC = 6.5 cm and ∠A = 120°.
Solution:
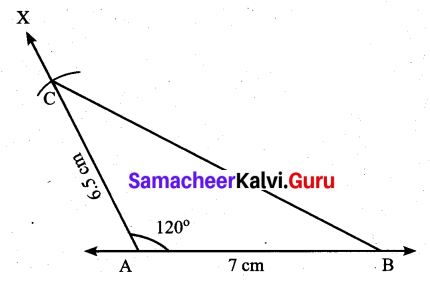
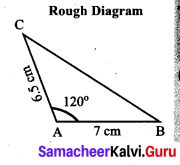
Construction:
Step 1: Drawn a line. Marked A and B on the line such that AB = 7 cm.
Step 2: At A, drawn a ray AX making an angle of 120° with AB.
Step 3: With A as centre, drawn an arc of radius 6.5 cm to cut the ray AX. Marked the point of intersection as C.
Step 4: Joined BC.
ABC is the required triangle.
(ii) BC = 8 cm, AC = 6 cm and ∠C = 40°.
Solution:
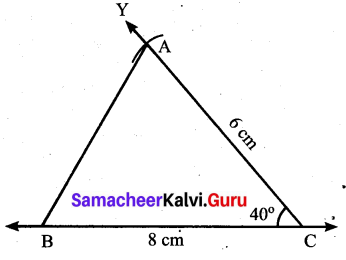
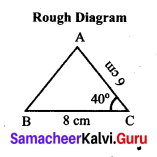
Construction:
Step 1: Drawn a line. Marked B and C on the line such fhat BC = 8 Cm.
Step 2: At C, drawn a ray CY making an angle of 40° with BC.
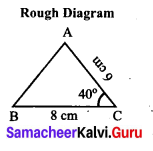
Step 3: With C as centre, drawn an arc of radius 6 cm to cut the ray CY, marked the point of intersection as A.
Step 4: Joined AB.
AB is the required triangle.
(iii) An isosceles obtuse triangle with equal sides 5 cm
Solution:
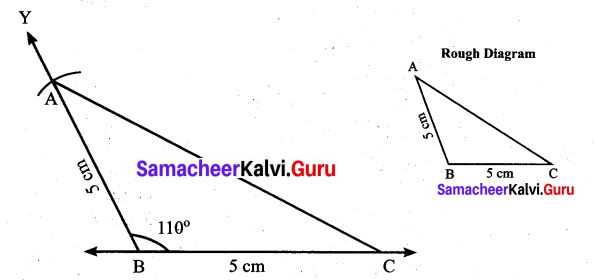
Construction:
Step 1: Drawn a line. Marked B and C on the line such that BC = 5 cm.
Step 2: At B drawn a ray BY making on obtuse angle 110° with BC.
Step 3: With B as centre, drawn an arc of radius 5 cm to cut ray BY. Marked the point of intersection as C.
Step 4: Joined BC. ABC is the required triangle.
![]()
III. Construct a triangle PQR with given conditions.
(i) ∠P = 60°, ∠R = 35° and PR = 7.8 cm
Solution:
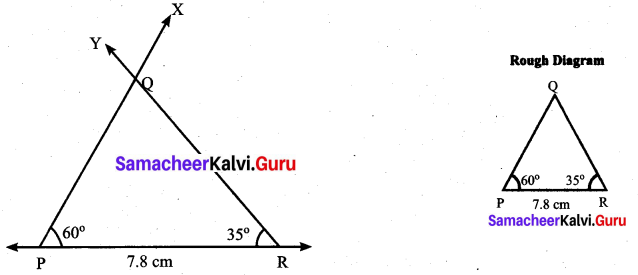
Construction:
Step 1: Drawn a line. Marked P and R on the line such that PR = 7.8 cm.
Step 2: At P, drawn a ray PX making an angle of 60° with PR.
Step 3: At R, drawn another ray RY making an angle of 35° with PR. Mark the point of intersection of the rays PX and RY as Q.
PQR is the required triangle.
(ii) ∠P = 115°, ∠Q = 40° and PQ = 6 cm
Solution:
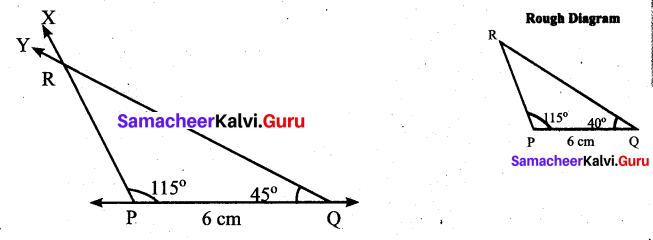
Construction:
Step 1: Drawn a line. Marked P and Q on the line such that PQ = 6 cm.
Step 2: At P, drawn O ray PX making an angle of 115° with PQ.
Step 3: At Q, drawn another ray QY making an angle of 40° with PQ. Marked the point of intersection of the rays PX and Q Y as R.
PQR is the required triangle.
(iii) ∠Q = 90°, ∠R = 42° and QR = 5.5 cm
Solution:
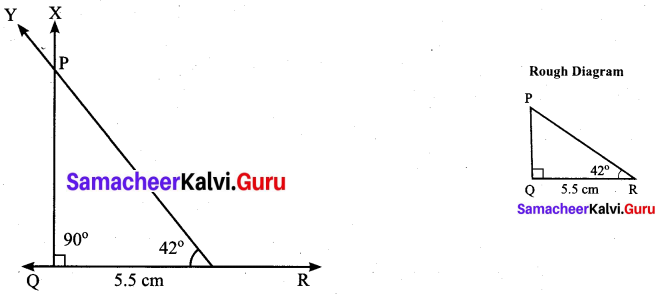
Construction:
Step 1: Drawn a line. Marked Q and R on the line such that QR = 5.5 cm.
Step 2: At Q, drawn a ray QX making an angle of 90° with QR.
Step 3: At R, drawn another ray RY making an angle of 42° QR. Marked the point of intersection of the rays QX and RY as P.
PQR is the required triangle.
Objective Type Questions
Question 8.
If two plans figures are congruent then they have
(i) same size
(ii) same shape
(iii) same angle
(iv) same shape and same size
Answer:
(iv) same shape and same size
Question 9.
Which of the following methods are used to check the congruence of plane figures?
(i) translation method
(ii) superposition method
(iii) substitution method
(iv) transposition method
Answer:
(ii) superposition method
Question 10.
Which of the following rule is not sufficient to verify the congruency of two triangles.
(i) SSS rule
(ii) SAS rule
(iii) SSA rule
(iv) ASA rule
Answer:
(iii) SSA rule
Question 11.
Two students drew a line segment each. What is the condition for them to be congruent?
(i) They should be drawn with a scale.
(ii) They should be drawn on the same sheet of paper.
(iii) They should have different lengths.
(iv) They should have the same length.
Answer:
(iv) They should have the same length.
Question 12.
In the given figure, AD = CD and AB = CB. Identify the other three pairs that are equal.
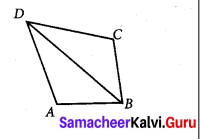
(i) ∠ADB = ∠CDB, ∠ABD = ∠CBD, BD = BD
(ii) AD = AB, DC = CB, BD = BD
(iii) AB = CD, AD = BC, BD = BD
(iv) ∠ADB = ∠CDB, ∠ABD = ∠CBD, ∠DAB = ∠DBC
Answer:
(i) ∠ADB = ∠CDB, ∠ABD = ∠CBD, BD = BD
Question 13.
In ∆ABC and ∆PQR, ∠A = 50° = ∠P, PQ = AB, and PR = AC. By which property ∆ABC and ∆PQR are congruent?
(i) SSS property
(ii) SAS property
(iii) ASA property
(iv) RHS property
Answer:
(ii) SAS property