Samacheer Kalvi 7th Maths Solutions Term 2 Chapter 3 Algebra Intext Questions

Students can Download Maths Chapter 3 Algebra Intext Questions and Answers, Notes Pdf, Samacheer Kalvi 7th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 7th Maths Solutions Term 2 Chapter 3 Algebra Intext Questions

Exercise 3.1

Try These (Text book Page No. 44)

Question 1.
Observe and complete the following table. First one is done for you.

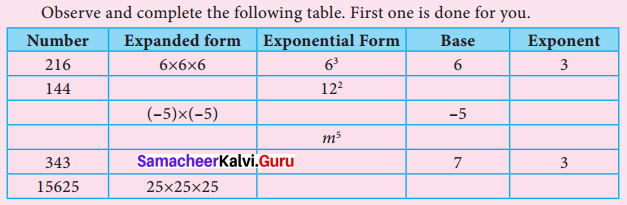
Solution:

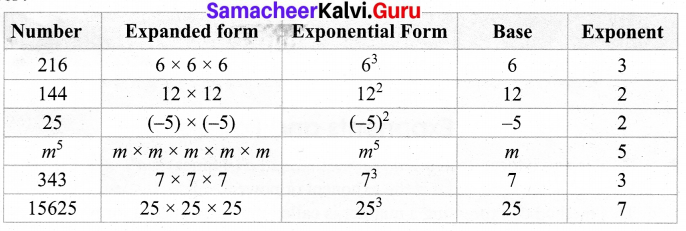
Try These (Text book Page No. 46)

Question 1.
Simplify and write the following in exponential form.
1. 2³ × 2⁵
2. p² × P⁴
3. x⁶ × x⁴
4. 3¹ × 3⁵ × 3⁴
5. (-1)² × (-1)³ × (-1)⁵
Solution:
1. 2³ × 2⁵ = 2³⁺⁵ = 2⁸ [since a^m × aⁿ = a^m+n]

2. p² × p⁴ = p²⁺⁴ = p⁶ [since a^m × aⁿ = a^m+n]

3. x⁶ × x⁴ = x⁶ + 4 = x¹⁰ [since a^m × aⁿ = a^m+n]

4. 3¹ × 3⁵ × 3⁴ = 3¹⁺⁵ × 3⁴ [since a^m × aⁿ = a^m+n]
= 3⁶ × 3⁴ [since a^m × aⁿ = a^m+n]
= 3¹⁰

5. (-1)² × (-1)³ × (-1)⁵
= (-1)²⁺³ × (-1)⁵ [Since a^m × aⁿ = a^m+n]
= (-1)⁵ × (-1)⁵
= (-1)⁵⁺⁵ [Since a^m × aⁿ = a^m+n]
= (-1)¹⁰

Try These (Text book Page No. 48)

Question 1.
Simply the following.
1. 23⁵ ÷ 23²
2. 11⁶ ÷ 11³
3. (-5)³ ÷ (-5)²
4. 7³ ÷ 7³
5. 15⁴ ÷ 15
Solution:

Try These (Text book Page No. 48)

Question 1.
Simplify and write the following in exponent form.
1. (3²)³
2. [(-5)³]²
3. (20⁶)²
4. (10³)⁵
Solution:
1. (3²)³ = 3^2×3 = 3⁶ [since (a^m)ⁿ = a^m×n]
2. [(-5)]² = (-5)^3×2 = (-5)⁶ [since (a^m)ⁿ = a^m×n]
3. (20⁶)² = 20^6×2 = 20¹² [since (a^m)ⁿ = a^m×n]
4. (10³)⁵ = 10^3×5 = 10¹⁵ [since (a^m)ⁿ = a^m×n]

Question 2.
Express the following exponent numbers using a^m × b^m = (a × b)^m.
(i) 5² × 3²
(ii) x³ × y³
(iii) 7⁴ × 8⁴
Solution:
(i) 5² × 3² = (5 × 3)² = 15² [since a^m × b^m = (a × b)^m]
(ii) x³ × y³ = (x × y)³ = (x y)³
(iii) 7⁴ × 8⁴ = (7 × 8)⁴ = 56⁴

Question 3.
Simplify the following exponent numbers by using (\(\frac { a }{ b } \))^m = \(\frac{a^{m}}{b^{m}}\)
(i) 5³ ÷ 2³
(ii) (-2)⁴ ÷ 3⁴
(iii) 8⁶ ÷ 5⁶
(iv) 6³ ÷ (-7)³
Solution:
(i) 5³ ÷ 2³ = (\(\frac { 5 }{ 2 } \))³ – [Since \(\frac{a^{m}}{b^{m}}\) = (\(\frac { a }{ b } \))^m]
(ii) (-2)⁴ ÷ 3⁴ = (\(\frac { -2 }{ 3 } \))⁴
(iii) 8⁶ ÷ 5⁶ = (\(\frac { 8 }{ 6 } \))⁶
(iv) 6³ ÷ (-7)³ = (\(\frac { 6 }{ -7 } \))³

Exercise 3.2

Try These (Text book Page No. 54)

Question 1.
Find the unit digit of the following exponential numbers:
(i) 106²¹
(ii) 25⁸
(iii) 31¹⁸
(iv) 20¹⁰
Solution:
(i) 106²¹ Unit digit of base 106 is 6 and the power is 21 and is positive.
Thus the unit digit of 106²¹ is 6.

(ii) 25⁸ Unit digit of base 25 is 5 and the power is 8 and is positive.
Thus the unit digit of 25⁸ is 5.

(iii) 31¹⁸ Unit digit of base 31 is 1 and the power 18 and is positive.
Thus the unit digit of 31¹⁸ is 1.

(iv) 20¹⁰ Unit digit of base 20 is 0 and the power 10 and is positive.
Thus the unit digit of 20¹⁰ is 0.

Try These (Text book Page No. 55)

Question 1.
Find the unit digit of the following exponential numbers:
(i) 64¹¹
(ii) 29¹⁸
(iii) 79¹⁹
(iv) 104³²
Solution:
(i) 64¹¹ Unit digit of base 64 is 4 and the power is 11 (odd power).
∴ Unit digit of 64¹¹ is 4.

(ii) 29¹⁸ Unit digit of base 29 is 9 and the power is 18 (even power).
Therefore, unit digit of 29¹⁸ is 1.

(iii) 79¹⁹ Unit digit of base 79 is 9 and the power is 19 (odd power).
Therefore, unit digit of 7919 is 9.

(iv) 104³² Unit digit of base 104 is 4 and the power is 32 (even power).
Therefore, unit digit of 104³² is 6.

Exercise 3.3

Try These (Text book Page No. 35)

Question 1.
Complete the following table:

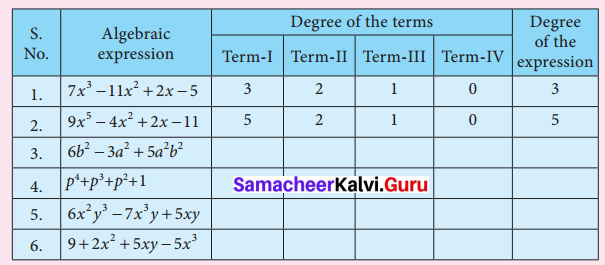
Solution:

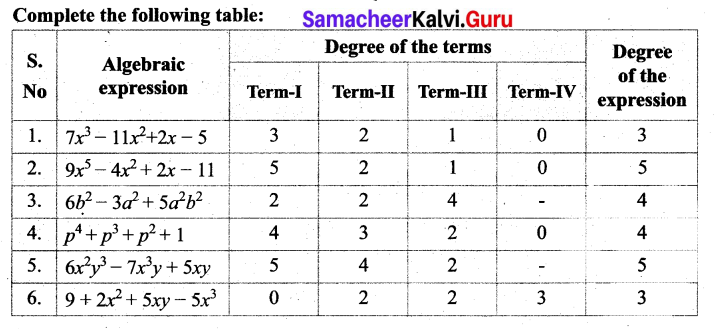
Question 2.
Identify the like terms from the following:
(i) 2x²y, 2xy²,3xy²,14x²y, 7yx
(ii) 3x³y², y³x, y³x², – y³x, 3y³x
(iii) 11pq, -pq, 11pqr, -11pq,pq
Solution:
(i) 2x²y, 2xy², 3xy², 14x²y, 7yx
(a) 2x²y and 14x²y are like terms.
(b) 2xy² and 3xy² are like terms.

(ii) 3x³y², y³x, y³x², – y³x, 3y³x
(a) y³x, – y³x and 3y³x are like terms.

(iii) 11 pq, -pq, 11pqr , -11 pq, pq
(a) 11 pq, -pq, -pq and pq are like terms.