Samacheer Kalvi 7th Maths Solutions Term 1 Chapter 5 Geometry Intext Questions

Students can Download Maths Chapter 5 Geometry Intext Questions and Answers, Notes Pdf, Samacheer Kalvi 7th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 7th Maths Solutions Term 1 Chapter 5 Geometry Intext Questions

Exercise 5.1

Recap
Try These (Text book Page No. 83)

Question 1.
Complete the following statements.
(i) A Line is a straight path that goes on endlessly in two directions.
(ii) A Line segment is a line with two end points.
(iii) A Ray is a straight path that begins at a point and goes on and extends endlessly the other direction.
(iv) The lines which intersect at right angles are Perpendicular lines.
(v) The lines which intersect each other at a point are called Intersecting lines.
(vi) The lines that never intersect are called Parallel lines.

Question 2.
Use a ruler or straightedge to draw each figure.

Question 3.
Look at the figure and answer the following questions.
(i) Which line is parallel to AB.
(ii) Name a line which intersect CD.
(iii) Name the lines which are perpendicular to GH
(iv) How many lines are parallel to IJ
(v) Will EF intersect AB? Explain.

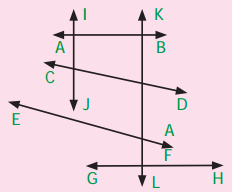
Solution:
\(\overleftrightarrow { GH } \) is parallel to \(\overleftrightarrow { AB } \)
(ii) \(\overleftrightarrow { IJ } \) and \(\overleftrightarrow { KL } \) intersect \(\overleftrightarrow { CD } \)
(iii) \(\overleftrightarrow { IJ } \) and \(\overleftrightarrow { KL } \) are perpendicular to \(\overleftrightarrow { GH } \)
(iv) Only one line \(\overleftrightarrow { KL } \) is parallel to \(\overleftrightarrow { IJ } \)
(v) Yes, \(\overleftrightarrow { EF } \) will intersect \(\overleftrightarrow { AB } \) at some point.

Try These (Text Book Page No. 85)

Choose the correct answer

Question 1.
A straight angle measures
(a) 45°
(b) 90°
(c) 180°
(d) 100°
Solution:
(c) 180°
Solution:
No, they are not adjacent pairs.

Question 2.
An angle with measure 128° is called ___ angle.
(a) a straight
(b) an obtuse
(c) an acute
(d) Right
Solution:
(b) an obtuse

Question 3.
The corner of the A4 paper has
(a) An acute angle
(b) A right angle
(c) Straight
(d) An obtuse angle
Solution:
(b) a right angle

Question 4.
If a perpendicular line is bisecting the given line, you would have two
(a) right angles
(b) obtuse angles
(c) acute angles
(d) reflex angles
Solution:
(a) right angle

Question 5.
An angle that measure 0° is called
(a) right angle
(b) obtuse angle
(c) acute angle
(d) Zero angle.
Solution:
(d) Zero angle

Try this (Text Book Page No. 86)

Question 1.
In each of the following figures, observe the pair of angles that are marked as ∠1 and ∠2. Do you think that they are adjacent pairs? Justify your answer.

Solution:
No, they are not adjacent pairs.
In (i) and (ii) angles ∠1 and ∠2 have no common vertex.
In (iii) the interiors of ∠1 and ∠2 overlaps.
∴ they are not adjacent angles.

Try these (Text book Page No. 87)

Question 1.
Few real life examples depicting adjacent angles are shown below.

Can you give three more examples of adjacent angles seen in real life?
Solution:

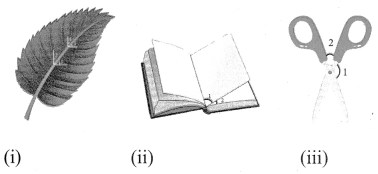
(i) Angles between leaf veins. [ ∠1 and ∠2],
(ii) Angles between adjacent pages of a book, when it is open [ ∠1 and ∠2 ].
(iii) Adjacent angles of scissors [ ∠1 and ∠2 ]

Question 2.
Observe the six angles marked in the picture shown. Write any four pairs of adjacent angles and that are not.
Solution:
Four pairs of adjacent angles are
1. ∠A and ∠B
2. ∠B and ∠C
3. ∠C and ∠D
4. ∠D and ∠E

Four pairs of non adjacent angles are.
1. ∠A and ∠C
2. ∠C and ∠F
3. ∠E and ∠D
4. ∠A and ∠F

Question 3.
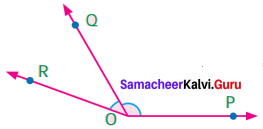
Identify the common arm, common vertex of the adjacent angles and shade the interior with two colours in each of the following figures.

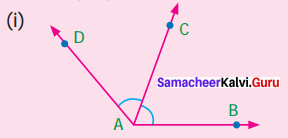
Solution:

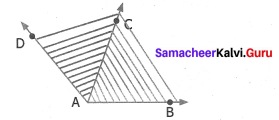
(ii)

Solution:

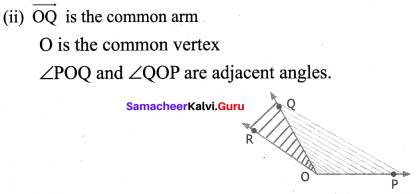
Question 4.
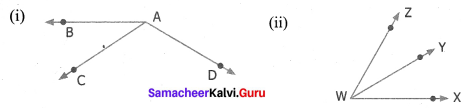
Name the adjacent angles in each of the following figure.

Solution:
(i) ∠BAC and ∠CAD are adjacent angles.
(ii) ∠XWY and ∠YWZ are adjacent angles.

Try These (Text Book Page No. 88)

Question 1.
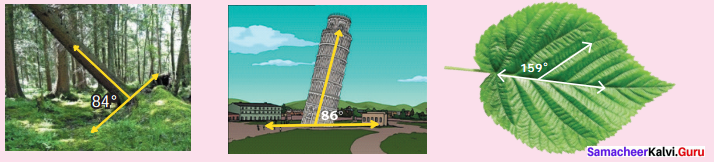
Observe the following pictures and find the other angles of the linear pair.

Solution:
(i) Given one angle 84°
∴ Other angle of the linear pair is 180° – 84° = 96°

(ii) One angle is given as 86°
Other angle of linear pair is 180° – 86° = 94°

(iii) Given one angle = 159°
Other angle of the linear pair = 180° – 159° = 21°

Try this (Text book Page No. 88)

Question 1.
Observe the figure. There are two angles namely ∠PQR = 150° and ∠QPS = 30° Is all this pair of supplementary angles a linear pair? Discuss

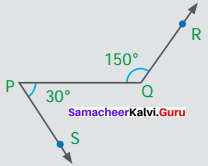
Solution:
Given ∠PQR =150°
∠QPS = 30°
They are supplementary angles,
But they are not adjacent angles as they don’t have common vertex or common arm.
∴ They are not a linear pair.

Try this (Text book Page No. 90)

Question 1.
What would happen to the angles if we add 3 or 4 or 5 rays on a line as given below?

Solution:
New adjacent angles are formed.
The new angles become smaller in measure. But their sum is 180° as it is a linear angle.

Try this (Text book Page No. 90)

Question 1.
Can you justify the statement
∠AOB + ∠BOC + ∠COD + ∠DOE + ∠EOF + ∠FOA = 360°?

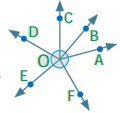
Solution:
We know that the sum of angles at a point is 360°
∠AOB + ∠BOC + ∠COD + ∠DOE + ∠EOF + ∠FOA = 360° as they are the sum of angles at the point ‘O’

Try These (Text book Page No. 91)

Question 1.
Four real life examples of vertically opposite angles are given below.

Solution:
(i) The four angles made in the scissors where the opposite angles are always equal.
(ii) The point where two roads intersect each other.
(iii) Rail road crossing signs.
(iv) An hourglass.

Question 2.
In the given figure two lines \(\overleftrightarrow { AB } \) and \(\overleftrightarrow { CD } \) intersect at ‘O’. Observe the pair of angles and complete the following table. One is done for you.

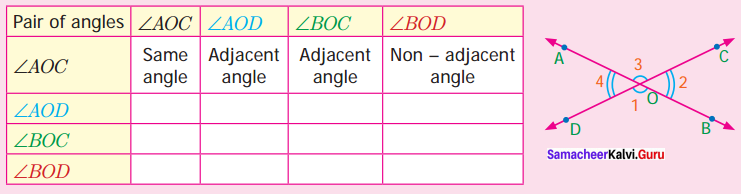
Solution:

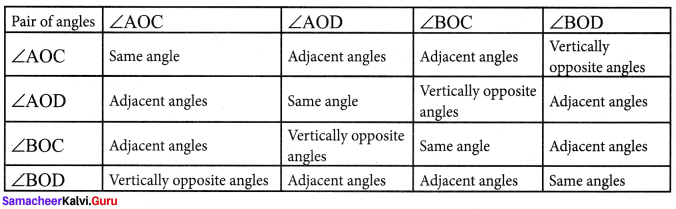
Question 3.
Name the two pairs of vertically opposite angles

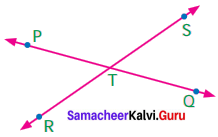
Solution:
∠PTS and ∠QTR are vertically opposite angles.
∠PTR and ∠QTS are vertically opposite angles.

Question 4.
Find the value of x° in the figure given below.

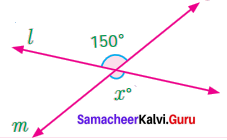
Solution:
Lines l and m intersect at a point and making a pair of vertically opposite angles x° and 150°.
We know that vertically opposite angles are equal.
x = 150°

Exercise 5.2

Try this (Text book Page No. 93)

Question 1.
For a given set of lines, it is possible to draw more than one transversal.

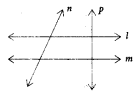
Solution:
Yes, it is possible to draw more than one transversal for a given set of lines. l and m are given set of lines. n and p are transversal

Try these (Text Book Page No 94)

Question 1.
Draw as many possible transversals in the given figures.

Solution:

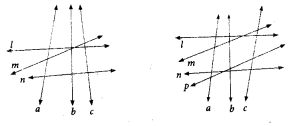
(i) a, b, c are transversal to l, m and n.
(ii) a, b, c are transversal to l, m, n and p. More transversals can be drawn.

Question 2.
Draw a line which is not the transversal to the above figures.
Solution:

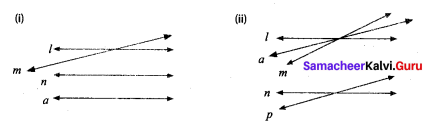
Question 3.
How many transversals can you draw for the following two lines

Solution:
Infinite number of transversals can be drawn.

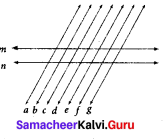
a, b, c, d, e, f, g are transversal to m and n.

Try these (Text book Page No. 96)

Question 1.
Four real life examples for transversal of parallel lines are given below.

Give four more examples for transversal of parallel lines seen in your surroundings.
Solution:
Some examples of parallel lines in our surroundings
(i) Zebra crossing on the road.
(ii) Railway tracks with sleepers.
(iii) Steps
(iv) Parallel bars in men’s gymnastics

Question 2.
Find the value of x.

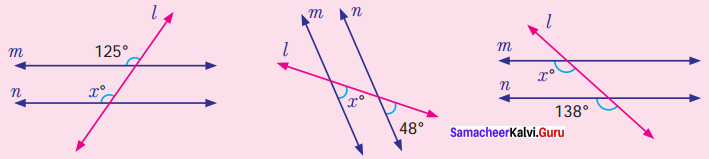
Solution:
(i) We know that if two parallel lines are cut by a transversal, each pair of corresponding angles are equal.
∴ x = 125°

(ii) m and n are parallel lines and l is a transversal x° and 48° are corresponding angles.
∴ x = 48°

(iii) m and n are parallel lines and 7’ is the transversal.
∴ Corresponding angles are equal.
∴ x° = 138°

Try these (Text book Page No. 98)

Question 1.
Find the value of x°.

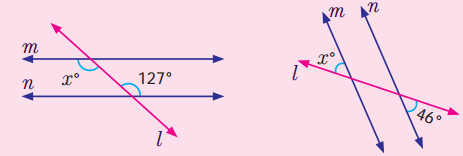
(i) m and n are parallel lines. ‘l’ is a transversal.
When two parallel lines are cut by a transversal each pair of alternate interior angles are equal.
∴ x° = 127°

(ii) m and n are parallel lines and l is the transversal.
When two parallel lines are cut by a transversal each pair of alternate exterior angles are equal.
∴ x° = 46°

Try These (Text Book Page No. 99)

Question 1.
Find the values of x.

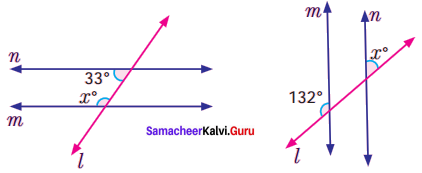
Solution:
(i) m and n are parallel lines and l is the transversal.
When two parallel lines are cut by a transversal, each pair of interior angles that lie on the same side of the transversal are supplementary

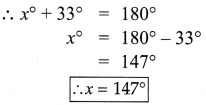
(ii) m and n are parallel line and l is the transversal.
When two parallel lines are cut by a transversal, each pair of exterior angles that lie on the same side of the transversal are supplementary.
the same side of the transversal are supplementary.
∴ x° + 132° = 180°
x° = 180° – 132°
= 48°
∴ x = 48°

Exercise 5.3

Question 1.
What will happen If the radius of the arc is less than half of AB?
Solution:

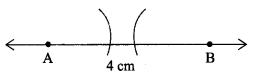
If the radius of the arc is less than half of AB, then both the arcs will not cut at a point
and we can’t draw perpendicular bisector.