Students can Download Maths Chapter 2 Measurements Ex 2.2 Questions and Answers, Notes Pdf, Samacheer Kalvi 7th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 7th Maths Solutions Term 1 Chapter 2 Measurements Ex 2.2
Question 1.
Find the area of rhombus PQRS shown in the following figures.
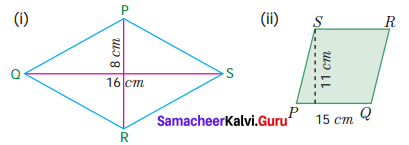
Solution:
(i) Given the diagonals d1 = 16 cm ; d2 = 8 cm
Area of the rhombus = \(\frac{1}{2}\)(d1 × d2) sq. units
= \(\frac{1}{2}\) × 16 × 8 cm2 = 64 cm2
Area of the rhombus = 64 cm2
(ii) Given base b = 15 cm ; Height h = 11 cm
Area of the rhombus = (base × height) sq. units
= 15 × 11 cm2 = 165 cm2
Area of the rhombus = 165 cm2
Question 2.
Find the area of a rhombus whose base is 14 cm and height is 9 cm.
Solution:
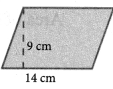
Given base b = 14 cm ; Height h = 9 cm
Area of the rhombus = b × h sq. units
= 14 × 9 cm2 = 126 cm2
Question 3.
Find the missing value.
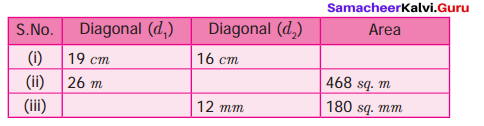
Solution:
(i) Given diagonal d1 = 19 cm ; d2 = 16 cm
Area of the rhombus = \(\frac{1}{2}\)(d1 × d2) sq. units = \(\frac{1}{2}\) × 19 × 16
= 152 cm2
(ii) Given diagonal d1 = 26 m ; Area of the rhombus = 468 sq. m
= \(\frac{1}{2}\)(d1 × d2) = 468 ; (26 × d2) = 468 × 2
d2 = \(\frac{468 \times 2}{26}\) = d2 = 36 m
(iii) Given diagonal d2 = 12 mm; Area of the rhombus = 180 sq. m
\(\frac{1}{2}\)(d1 × d2) = 180
\(\frac{1}{2}\)(d1 × 12) = 180
d1 × 12 = 180 × 2
d1 = \(\frac{180 \times 2}{12}\)
d1 = 30 mm
Diagonal d1 = 30 mm
Tabulating the results we have
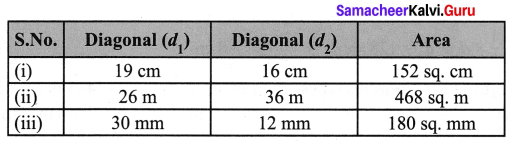
Question 4.
The area of a rhombus is 100 sq. cm and length of one of its diagonals is 8 cm. Find the length of the other diagonal.
Solution:
Given the length of one diagonal d1 = 8 cm ; Area of the rhombus = 100 sq. cm
\(\frac{1}{2}\)(d1 × d2) = 100
\(\frac{1}{2}\) × 8 × d2 = 100
8 × d2 = 100 × 2
d2 = \(\frac{100 \times 2}{8}\) = 25 cm
Length of the other diagonal d2 = 25 cm
![]()
Question 5.
A sweet is in the shape of rhombus whose diagonals are given as 4 cm and 5 cm. The surface of the sweet should be covered by an aluminum foil. Find the cost of aluminum foil used for 400 such sweets at the rate of ₹ 7 per 100 sq. cm.
Solution:
Diagonals d1 = 4 cm and d2 = 5 cm
Area of one rhombus shaped sweet = \(\frac{1}{2}\)(d1 × d2) sq. units = \(\frac{1}{2}\) × 4× 5 cm2 = 10 cm2
Aluminum foil used to cover 1 sweet = 10 cm2
∴ Aluminum foil used to cover 400 sweets = 400 × 10 = 4000 cm2
Cost of aluminum foil for 100 cm2 = ₹ 7
∴ Cost of aluminum foil for 4000 cm2 = \(\frac{4000}{100}\) × 7 = ₹ 280
∴ Cost of aluminum foil used = ₹ 280.
Objective Type Questions
Question 6.
The area of the rhombus with side 4 cm and height 3 cm is
(i) 7 sq. cm
(ii) 24 sq. cm
(iii) 12 sq. cm
(iv) 10 sq. cm
Solution:
(iii) 12 sq. cm
Hint:
Area = Base × Height = 4 × 3 = 12 cm2
Question 7.
The area of the rhombus when both diagonals measuring 8 cm is
(i) 64 sq. cm
(ii) 32 sq. cm
(iii) 30 sq. cm
(iv) 16 sq. cm
Solution:
(ii) 32 sq. cm
Hint:
Area = \(\frac{1}{2}\)(d1 × d2) = \(\frac{1}{2}\) × 8 × 8 = 32
Question 8.
The area of the rhombus is 128 sq. cm. and the length of one diagonal is 32 cm. The length of the other diagonal is
(i) 12 cm
(ii) 8 cm
(iii) 4 cm
(iv) 20 cm
Solution:
(ii) 8 cm
Hint:
\(\frac{1}{2}\) × d1 × d2 = 128 ⇒ d2 = \(\frac{128 \times 2}{32}\) = 8cm
![]()
Question 9.
The height of the rhombus whose area 96 sq. m and side 24 m is
(i) 8 m
(ii) 10 m
(iii) 2 m
(iv) 4 m
Solution:
(iv) 4 m
Hint:
Area = Base × height = 96 ⇒ height = \(\frac{96}{24}\) = 4
Question 10.
The angle between the diagonals of a rhombus is
(i) 120°
(ii) 180°
(iii) 90°
(iv) 100°
Solution:
(iii) 90°
Hint:
Angles of a rhombus bisect at right angles.