You can Download Samacheer Kalvi 6th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
![]()
Tamilnadu Samacheer Kalvi 6th Maths Solutions Term 2 Chapter 1 Numbers Ex 1.3
Miscellaneous Practice Problems
Question 1.
Every even number greater than 2 can be expressed as the sum of two prime numbers. Verify this statement for every even number up to 16.
Solution:
4 = 2 + 2
6 = 3 + 3
8 = 3 + 5
10 = 3 + 7
12 = 5 + 7
14 = 3 + 11
16 = 3 + 13
Question 2.
Is 173 a prime? Why?
Solution:
yes, because it has two factors.
Question 3.
For which of the numbers, from n = 2 to 8, is 2n – 1 a prime?
Solution:
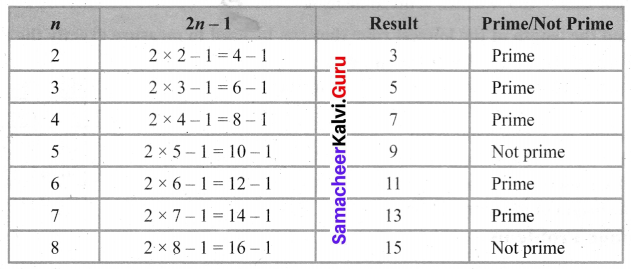
For n = 2, 3, 4, 6 and 7 it is prime.
Question 4.
Explain your answer with the reason for the following statements.
(i) A number is divisible by 9 if it is divisible by 3.
(ii) A number is divisible by 6 if it is divisible by 12.
Solution:
(i) False, 42 is divisible by 3 but it is not divisible by 9
(ii) True, 36 is divisible by 12. Also divisible by 6.
![]()
Question 5.
Find A as required
(i) The greatest 2 digit number 9A is divisible by 2.
(ii) The least number 567A is divisible by 3.
(iii) The greatest 3 digit number 9A6 is divisible by 6.
(iv) The number A08 is divisible by 4 and 9.
(v) The number 225A85 is divisible by 11.
Solution:
(i) A number is divisible by 2 if it is an even number.
The greatest 2 digit even number is 98.
∴ A = 8
(ii) A number is divisible by 3 if the sum of its digits is divisible by 3
Sum of digits of 567A = 5 + 6 + 7+ A = 18 + A
∴ 18 is divisible by 3
∴ A maybe 0
The number will be 5670
(iii) A number is divisible by 6 if it is divisible by both 2 and 3
9A6 is even and so divisible by 2
If A = 9 then the sum of digits will be = 24 which is divisible by 3.
The number will be 996 and A = 9
(iv) 08 is divisible by 4, so A08 is divisible by 4.
If A = 1 then the sum of digits will be 9 which is divisible by 9.
The number will be 108 and A = 1
(v) 5 + A + 2 – (8 + 5 + 2) = 7 + A – 15 = -8 + A
∴ A = 8
Question 6.
Numbers divisible by 4 and 6 are divisible by 24. Verify this statement and support your answer with an example.
Solution:
False 12 is divisible by both 4 and 6. But not divisible by 24
Question 7.
The sum of any two successive odd numbers ir always divisible by 4. Justify this statement with an example.
Solution:
True.
The sum of any two consecutive odd numbers is divisible by 4
For example 11 + 13 = 24, divisible by 4
Also, all the consecutive odd numbers are of the form 4n + 1 or 4n + 3
Their sum = 4x + 4 which is divisible by 4.
Question 8.
Find the length of the longest rope that can be used to measure exactly the ropes of length lm 20 cm, 3m 60 cm and 4 m.
Solution:
Length of ropes are 4 m, 3 m 60 cm and lm 20 cm = 400 cm, 360 cm, 120 cm
Finding HCF (400, 360, 120)
10, 9 and 3 has no common divisor
HCF (400, 360, 120) = 2 × 2 × 2 × 5 = 40
The length of the rope will be 40 cm

![]()
Challenge Problems
Question 9.
The sum of three prime numbers is 80. The difference between the two of them is 4. Find the numbers.
Solution:
Three prime numbers 2, 37, 41
Sum 2 + 37+ 41 = 80
The difference between the two of them 41 – 37 = 4
Question 10.
Find the sum of all the prime numbers between 10 and 20 and check whether that sum is divisible by all the single-digit numbers.
Solution:
prime numbers between 10 and 20
11, 13, 17, 19
Sum 11 + 13 + 17 + 19 = 60
60 is divisible by 1, 2, 3, 4, 5, 6
Question 11.
Find the smallest number which is exactly divisible by all the numbers from 1 to 9.
Solution:
To find the smallest number we have to Find the LCM (1, 2, 3, 4, 5, 6, 7, 8, 9)
LCM is 2 × 3 × 2 × 5 × 7 × 2 × 3 = 2520
The required number is 2520

Question 12.
The product of any three consecutive number is always divisible by 6. Justify this statement with an example.
Solution:
Yes. Because one of every two consecutive integers is even and so the product of three consecutive integers is even and divisible by 2.
Also one of every 3 consecutive integers is divisible by 3.
Product of any three consecutive integers is divisible by 6.
Example: 5 × 6 × 7
Question 13.
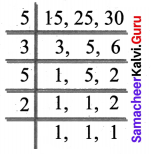
Malarvizhi, Karthiga, and Anjali are friends and natives of the same village. They work in different places. Malarvizhi comes to her home once in 5 days. Similarly, Karthiga and Anjali come to their homes once in 6 days and 10 days respectively. Assuming that they met each other on the 1st of October, when will all the three again?
Solution:
Find the LCM (5, 6, 10)
LCM (15, 25, 30) = 5 × 6 = 30
They meet again after 30 days
∴ They met on 1st October
They will meet again on 31st October
Question 14.
In an apartment consisting of 108 floors, two lifts A & B starting from the ground floor, stop at every 3rd and 5th floor respectively. On which floors, will both of them stop together?
Solution:
Multiples of 3 are 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, 39, 42, 45, 48, 51, 54, 57, 60, 63, 66, 69, 72, 75, 78, 81, 84, 87, 90, 93, 96, 99, 102, 105
Multiples of 5 are 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65, 70, 75, 80, 85, 90, 95, 100, 105
Common multiples of 3 and 5 are 15, 30, 45, 60, 75, 90 and 105
Both the lifts will stop at floors 15, 30, 45, 60, 75, 90 and 105
![]()
Question 15.
The product of 2 two-digit numbers is 300 and their HCF is 5. What are the numbers?
Solution:
Given that HCF of 2 numbers is 5
The numbers may like 5x and 5y
Also given their product = 300
5x × 5y = 300
⇒ 25xy = 300
⇒ \(x y=\frac{300}{25}\)
⇒ xy = 12
The possible values of x andy be (1, 12) (2, 6) (3, 4)
The numbers will be (5x, 5y)
⇒ (5 × 1, 5 × 12) = (5, 60)
⇒ (5 × 2, 5 × 6) = (10, 30)
⇒ (5 × 3, 5 × 4) = (15, 20)
(5, 60) is impossible because the given the numbers are two digit numbers.
The remaining numbers are (10, 30) and (15, 20)
But given that HCF is 5
(10, 30) is impossible, because its HCF = 10
The numbers are 15, 20
Question 16.
Find whether the number 564872 is divisible by 88?
Solution:
872 is divisible by 8.
Hence 56 + 872 is divisible by 8
(2 + 8 + 6) – (7 + 4 + 5) = 16 – 16 = 0
∴ 564872 is divisible by 11
∴ 564872 is divisible by 88.
Question 17.
Wilson, Mathan, and Guna can complete one round of a circular track in 10, 15, and 20 minutes respectively. If they start together at 7 a.m from the starting point, at what time will they meet together again at the starting point?
Solution:
LCM (10, 15, 20) = 60
∴ They will meet at 8 a.m