You can Download Samacheer Kalvi 12th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 7 Applications of Differential Calculus Ex 7.10
Choose the correct or the most suitable answer.
Question 1.
The volume of a sphere is increasing in volume at the rate of 3πcm3/sec. The rate of change of its radius when radius is \(\frac{1}{2}\) cm …….
(a) 3 cm/s
(b) 2 cm/s
(c) 1 cm/s
(d) \(\frac{1}{2}\) cm/s
Solution:
(a) 3 cm/s
Hint:

Question 2.
A balloon rises straight up at 10 m/s. An observer is 40 m away from the spot where the balloon left the ground. Find the rate of change of the balloon’s angle of elevation in radian per second when the balloon is 30 metres above the ground.

Solution:
(b) \(\frac{4}{25}\) radian/sec
Hint:
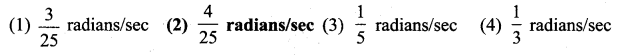
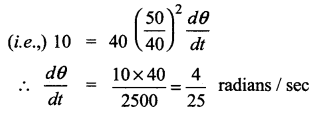
![]()
Question 3.
The position of a particle moving along a horizontal line of any time t is given by s(t) = 80t – 16t2. The time at which the particle is at rest is …….
![]()
Solution:
(2) t = \(\frac{1}{3}\)
Hint:
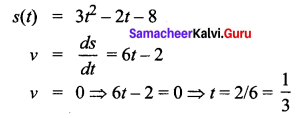
Question 4.
A stone is thrown up vertically. The height reaches at time t seconds is given by x = 80t – 16t2. The stone reaches the maximum height in time t seconds is given by …..
(a) 2
(b) 2.5
(c) 3
(d) 3.5
Solution:
(b) 2.5
Hint:

Question 5.
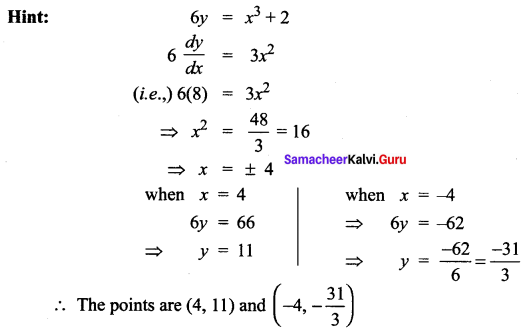
Find the point on the curve 6y = x3 + 2 at which y-coordinate changes 8 times as fast as x-coordinate is …….
(a) (4, 11)
(b) (4, -11)
(c) (-4, 11)
(d) (-4, -11)
Solution:
(a) (4, 11)
Question 6.
The abscissa of the point on the curve f(x) = \(\sqrt{8-2 x}\) at which the slope of the tangent is -0.25?
(a) -8
(b) -4
(c) -2
(d) 0
Solution:
(b) -4

Question 7.
The slope of the line normal to the curve f(x) = 2cos 4x at x = \(\frac{\pi}{2}\) is ……..

Solution:
(c) \(\frac{\sqrt{3}}{12}\)

![]()
Question 8.
The tangent to the curve y2 – xy + 9 = 0 is vertical when
![]()
Solution:
(b) \(y=\pm \sqrt{3}\)
Hint:

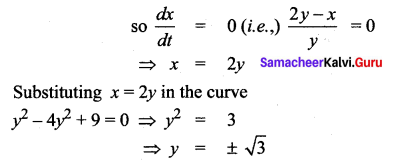
Question 9.
Angle between y2 = x and x2 = y at the origin is ……
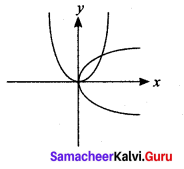
Solution:
(c) \(\frac{\pi}{2}\)
Hint:
The angle between the parabolas is the angle between the axes = \(\frac{\pi}{2}\)
Question 10.
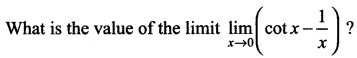
(a) 0
(b) 1
(c) 2
(d) ≤
Solution:
(a) 0
Hint:

Question 11.
The function sin4 x + cos4 x is increasing in the interval
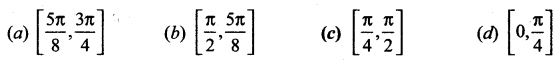
Solution:
(c) \(\left[\frac{\pi}{4}, \frac{\pi}{2}\right]\)
Hint:
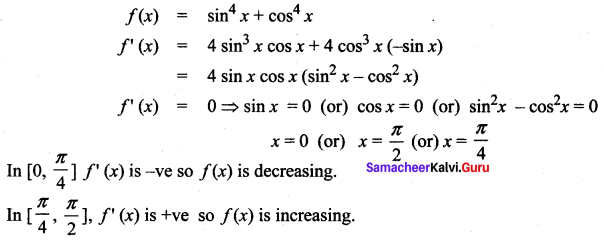
Question 12.
The number given by the Rolle’s theorem for the function x3 – 3x2, x ∈ [0, 3] is ………
(a) 1
(b) \(\sqrt{2}\)
(c) \(\frac{3}{2}\)
(d) 2
Solution:
(d) 2
Hint:
![]()
![]()
Question 13.
The number given by the Mean value theorem for the function \(\frac{1}{x}\), x ∈ [1, 9] is …..
(a) 2
(b) 2.5
(c) 3
(d) 3.5
Solution:
(c) 3
Hint:

Question 14.
The minimum value of the function |3 – x | + 9 is ………
(a) 0
(b) 3
(c) 6
(d) 9
Solution:
(d) 9
Hint:
f(x) = |3 – x| + 9
Minimum value of |3 – x| = 0
Minimum value of |3 – x| + 9 = 0 + 9 = 9
Question 15.
The maximum slope of the tangent to the curve y = ex sin x, x ∈ [0, 2n] is at …………
![]()
Solution:
(b) \(x=\frac{\pi}{2}\)
Hint:
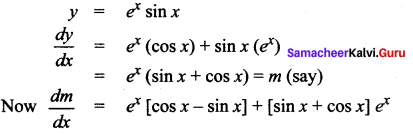
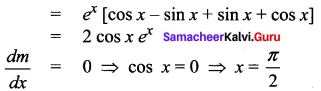
Question 16.
The maximum value of the function x2e-2x, x > 0 is ……..
![]()
Solution:
(c) \(\frac{1}{e^{2}}\)
Hint:

Question 17.
One of the closest points on the curve x2 – y2 = 4 to the point (6, 0) is ……..
![]()
Solution:
(c) \((3, \sqrt{5})\)
Hint:
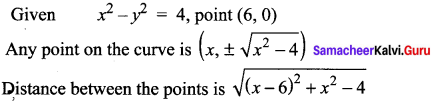
Substituting all the given options we get minimum distance point \((3, \sqrt{5})\)
Question 18.
The maximum product of two positive numbers, when their sum of the squares is 200, is ……..
(a) 100
(b) \(25 \sqrt{7}\)
(c) 28
(d) \(24 \sqrt{14}\)
Solution:
(a) 100
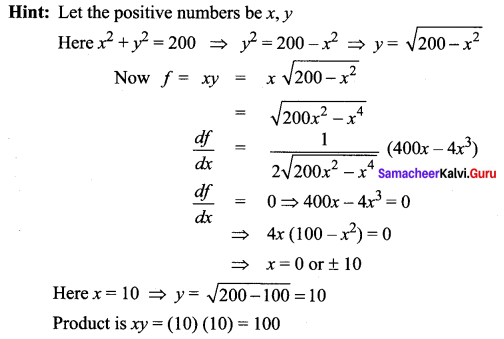
Question 19.
The curves = ax4 + bx2 with ab > 0
(a) has no horizontal tangent
(b) is concave up
(c) is concave down
(d) has no points of inflection
Solution:
(d) has no points of inflection
Question 20.
The point of inflection of the curve y = (x – 1)3 is ……….
(a) (0, 0)
(b) (0, 1)
(c) (1, 0)
(d) (1, 1)
Solution:
(c) (1, 0)
Hint:

Samacheer Kalvi 12th Maths Solutions Chapter 7 Applications of Differential Calculus Ex 7.10 Additional Questions Solved
Question 1.
The gradient of the curve y = – 2x3 + 3x + 5 at x = 2 is ………
(a) -20
(b) 27
(c) -16
(d) -21
Solution:
(d) -21
Hint:
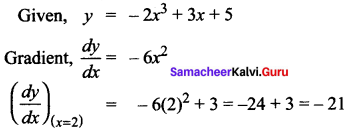
![]()
Question 2.
The rate of change of area A of a circle of radius r is ……..
![]()
Solution:
(b) \(2 \pi r \frac{d r}{d t}\)
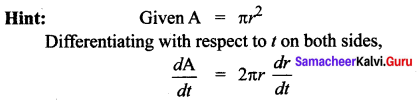
Question 3.
Aspherical snowball is melting in such a way that its volume is decreasing at a rate of 1 cm3/min. The rate at which the diameter is decreasing when the diameter is 10 cms is …………….
![]()
Solution:
(a) \(\frac{-1}{50 \pi} \mathbf{c m} / \mathbf{m i n}\)

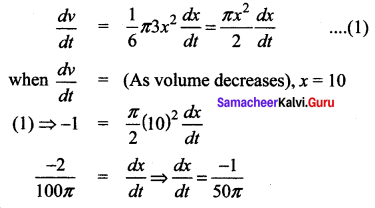
Question 4.
![]()

Solution:
(b) \(x=a \cos ^{3} \theta ; y=a \sin ^{3} \theta\)
Hint:
![]()
Question 5.
If the normal to the curve \(x^{2 / 3}+y^{2 / 3}=a^{2 / 3}\) makes an angle θ with the x-axis then the slope of the normal is ……..
(a) – cot θ
(b) tan θ
(c) – tan θ
(d) cot θ
Solution:
(b) tan θ
Hint:
Since the normal to the curve makes an angle θ with the x-axis.
The slope of the normal = tan θ
Question 6.
What is the surface area of a sphere when the volume is increasing at the same rate as its radius?
(a) 1
(b) \(\frac{1}{2 \pi}\)
(c) 4π
(d) \(\frac{4 \pi}{3}\)
Solution:
(a) 1
Hint:

Question 7.
For what values of x is the rate of increase of x3 – 2x2 + 3x + 8 is twice the rate of increase of x.
![]()
Solution:
(d) \(\left(\frac{1}{3}, 1\right)\)
Hint:

![]()
Question 8.
If the volume of an expanding cube is increasing at the rate of 4cm3/sec then the rate of change of surface area when the volume of the cube is 8 cubic cm is …….
(a) 8cm2/sec
(b) 16cm2/sec
(c) 2cm2/sec
(d) 4cm2/sec
Solution:
(a) 8cm2/sec
Hint:
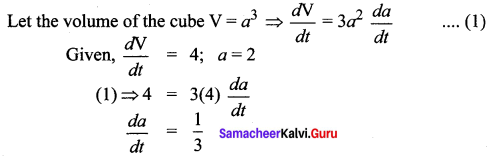
Let the surface area of the cube S = 6a2
Question 9.
If a normal makes an angle θ with a positive x-axis then the slope of the curve at the point where the normal is drawn is ……..
(a) -cot θ
(b) tan θ
(c) -tan θ
(d) cot θ
Solution:
(a) -cot θ
Hint:
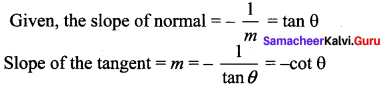
Question 10.
If the velocity of a particle moving along a straight line is directly proportional to the square of its distance from a fixed point on the line. Then its acceleration is proportional to …….
(a) s
(b) s2
(c) s3
(d) s4
Solution:
(c) s3
Hint:
Let s be the distance of the particle from a fixed point on the line at a time at t and V be the velocity.
Then V ∝ s2
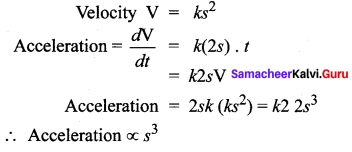
Question 11.
The Rolle’s constant for the function y = x2 on [-2, 2] is …………..

Solution:
(b) 0
Hint:
Let f(x) = y = x2
f'(x) = 2x = 0
By Rolle’s theorem there exists a ‘c’ such that
f'(c) = 0
⇒ 2c = 0
⇒ c = 0 ∈ (-2, 2)
Question 12.
The value ‘c’ of Lagranges Mean Value Theorem for f(x) = \(\sqrt{x}\) when a = 1 and b = 4 is ………
![]()
Solution:
(a) \(\frac{9}{4}\)
Hint:
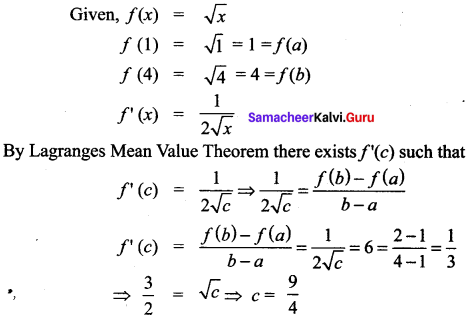
![]()
Question 13.
In a given semi circle of diameter 4 cm, a rectangle is to be inscribed. The maximum area of the rectangle is ……..
(a) 2
(b) 4
(c) 8
(d) 16
Solution:
(b) 4
Hint:
Let the side of the rectangle be ‘a’ cm
The maximum rectangle inscribed in a circle is a square.
The diagonal of the rectangle = 4 cm
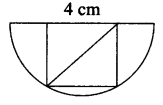
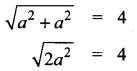
2a2 = 16
a2 = 8 cm
The maximum area = 8
Half of the area of the square = 4 cm
Question 14.
The least possible perimeter of a rectangle of area 100 m2 is ……..
(a) 10
(b) 20
(c) 40
(d) 60
Solution:
(c) 40
Hint:
Let the length of the rectangle = x m
Let the length of the breadth = y m

The least perimeter = 2(x + y) = 2(10 + 10) = 40 cm
Question 15.
Which of the following curves is concave down?
(a) y = -x2
(b) y = x2
(c) y = ex
(d) y = x2 + 2x – 3
Solution:
(a) y = -x2

![]()
Question 16.
The point of inflection of the curve y = x4 is at …….
(a) x = 0
(b) x = 3
(c) x = 12
(c) no where
Solution:
(a) x = 0
Hint:
