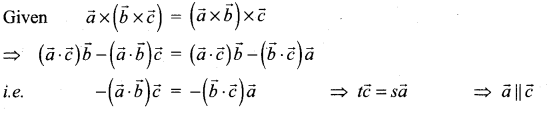You can Download Samacheer Kalvi 12th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 6 Applications of Vector Algebra Ex 6.10
Choose the correct or the most suitable answer from the given four alternatives:
Question 1.
If \(\vec{a}\) and \(\vec{b}\) are parallel vector, then \([\vec{a}, \vec{c}, \vec{b}]\) is equal to ………………..
(a) 2
(b) -1
(c) 1
(d) 0
Solution:
(d) 0
Hint:
\(\vec{a}\) and \(\vec{b}\) are parallel vectors, so \(\vec{a} \times \vec{b}\) = 0
then \([\vec{a} \vec{c} \vec{b}]=-[\vec{a} \vec{b} \vec{c}]=-(\vec{a} \times \vec{b}) \cdot \vec{c}\) = 0
Question 2.
If a vector \(\vec{\alpha}\) lies in the plane of \(\vec{\beta}\) and \(\vec{\gamma}\), then …………
![]()
Solution:
(c) \([\vec{\alpha}, \vec{\beta}, \vec{\gamma}]\) = 0
Hint:
Since \([\vec{\alpha}, \vec{\beta}, \vec{\gamma}]\) are lie in the same plane
so \([\vec{\alpha}, \vec{\beta}, \vec{\gamma}]\) = 0
Question 3.
If \(\vec{a} \cdot \vec{b}=\vec{b} \cdot \vec{c}=\vec{c} \cdot \vec{a}\)= 0, then the value of \(|[\vec{a}, \vec{b}, \vec{c}]|\) is ……………….
(a) \(|\vec{a}||\vec{b}||\vec{c}|\)
(b) \(\frac{1}{3}|\vec{a}||\vec{b}||\vec{c}|\)
(c) 1
(d) -1
Solution:
(a) \(|\vec{a}||\vec{b}||\vec{c}|\)
Hint:

![]()
Question 4.
If \(\vec{a}, \vec{b}, \vec{c}\) are three unit vectors such that \(\vec{a}\) is perpendicular to \(\vec{b}\), and is parallel to \(\vec{c}\) then \(\vec{a} \times(\vec{b} \times \vec{c})\)is equal to ………………….
(a) \(\vec{a}\)
(b) \(\vec{b}\)
(c) \(\vec{c}\)
(d) \(\vec{0}\)
Solution:
(b) \(\vec{b}\)
Hint:

Question 5.
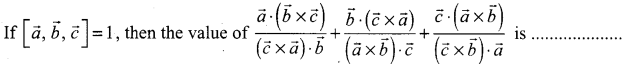
(a) 1
(b) -1
(c) 2
(d) 3
Solution:
(a) 1
Hint:

Question 6.
The volume of the parallelepiped with its edges represented by the vectors \(\hat{i}+\hat{j}, i+2 \hat{j}\), \(\hat{i}+\hat{j}+\pi \hat{k}\) is ……………

Solution:
(c) π
Hint:
Volume = \([\vec{a} \vec{b} \vec{c}]=\left|\begin{array}{ccc}{1} & {1} & {0} \\ {1} & {2} & {0} \\ {1} & {1} & {\pi}\end{array}\right|\)
= π(2 – 1) = π cubic units
![]()
Question 7.
If \(\vec{a}\) and \(\vec{b}\) are unit vectors such that \([\vec{a}, \vec{b}, \vec{a} \times \vec{b}]=\frac{\pi}{4}\) then the angle between \(\vec{a}\) and \(\vec{b}\) is …………

Solution:
(a) \(\frac{\pi}{6}\)
Hint:
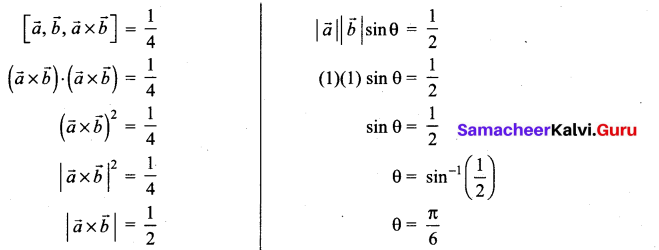
Question 8.
![]()
(a) 0
(b) 1
(c) 6
(d) 3
Solution:
(a) 0
Hint:
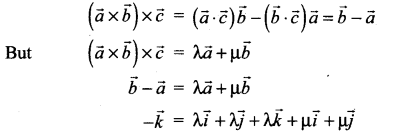
Equate corresponding coefficients on both sides
λ + µ = 0 and λ = -1 this gives µ = 1
∴ Then the value of λ + µ = 0.
Question 9.
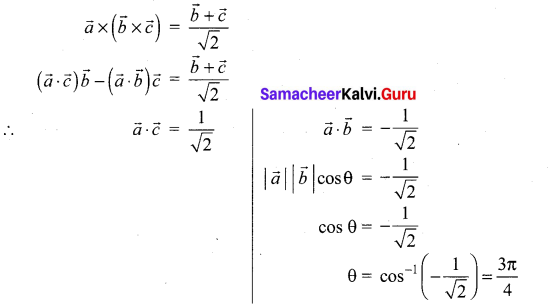
If \(\vec{a}, \vec{b}, \vec{c}\) are three non-coplanar vectors such that \(\vec{a} \times(\vec{b} \times \vec{c})=\frac{\vec{b}+\vec{c}}{\sqrt{2}}\), then the angle between \(\vec{a}\) and \(\vec{b}\) is …………
(a) 81
(b) 9
(c) 27
(d) 18
Solution:
(a) 81
Hint:
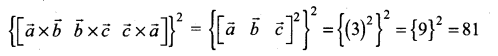
Question 10.
Solution:
(b) \(\frac{3 \pi}{4}\)
Hint:
Question 11.
If the volume of the parallelepiped with \(\vec{a} \times \vec{b}, \vec{b} \times \vec{c}, \vec{c} \times \vec{a}\) as coterminous edges is 8 cubic units, then the volume of the parallelepiped with \((\vec{a} \times \vec{b}) \times(\vec{b} \times \vec{c}),(\vec{b} \times \vec{c}) \times(\vec{c} \times \vec{a})\) and \((\vec{c} \times \vec{a}) \times(\vec{a} \times \vec{b})\) as coterminous edges is ………………
(a) 8 cubic units
(b) 512 cubic units
(c) 64 cubic units
(d) 24 cubic units
Solution:
(c) 64 cubic units
Hint:
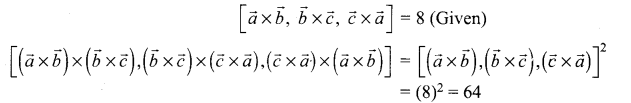
![]()
Question 12.
Consider the vectors \(\vec{a}, \vec{b}, \vec{c}, \vec{d}\) such that \((\vec{a} \times \vec{b}) \times(\vec{c} \times \vec{d})=\overrightarrow{0}\). Let P1 and P2 be the planes determined by the pairs of vectors \(\vec{a}, \vec{b}\) and \(\vec{c}, \vec{d}\) respectively. Then the angle between P1 and P2 is ……………..
(a) 0°
(b) 45°
(c) 60°
(d) 90°
Solution:
(a) 0°
Hint:
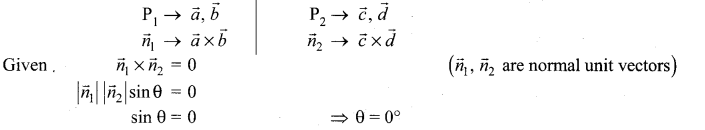
Question 13.
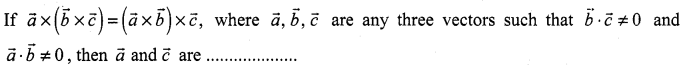
(a) perpendicular
(b) parallel
(c) inclined at an angle \(\frac{\pi}{3}\)
(d) inclined at an angle \(\frac{\pi}{6}\)
Solution:
(b) parallel
Hint:
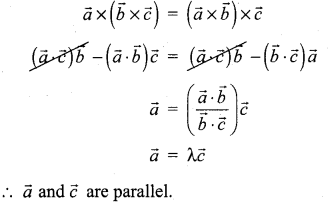
Question 14.
If ![]() , then a vector perpendicular to \(\vec{a}\) and lies in the plane containing \(\vec{b}\) and \(\vec{c}\) is
, then a vector perpendicular to \(\vec{a}\) and lies in the plane containing \(\vec{b}\) and \(\vec{c}\) is

Solution:
(d) \(-17 \hat{i}-21 \hat{j}-97 \hat{k}\)
Hint:

Question 15.
The angle between the lines ![]() is ………..
is ………..
![]()
Solution:
(d) \(\frac{\pi}{2}\)
Hint:
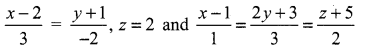

![]()
Question 16.
If the line ![]() lies in the plane x + 3 + αz + β = 0, then (α, β) is …………..
lies in the plane x + 3 + αz + β = 0, then (α, β) is …………..
(a) (-5, 5)
(b) (-6, 7)
(c) (5, -5)
(d) (6, -7)
Solution:
(d) (-6, 7)
Hint:
d.c.s of the first line = (3, -5, 2)
d.c.s of the line perpendicular to plane = (1, 3, -α)
a1a2 + b1b2 + c1c2 = 0
3 – 15 – 2α = 0 => -12 – 2α = 0
-2α =12 => α = -6
Plane passes through the point (2, 1, -2) so
2 + 3 + 6(-2) + β = 0 => β = 7
(α, β) = (-6, 7)
Question 17.
The angle between the line \(\vec{r}=(\hat{i}+2 \hat{j}-3 \hat{k})+t(2 \hat{i}+\hat{j}-2 \hat{k})\) and the plane \(\vec{r} \cdot(\hat{i}+\hat{j})+4\) = 0 is ……………
(a) 0°
(b) 30°
(c) 45°
(d) 90°
Solution:
(c) 45°
Hint:
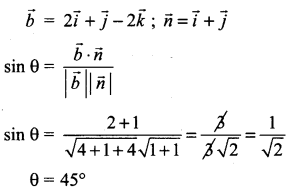
Question 18.
The coordinates of the point where the line \(\vec{r}=(6 \hat{i}-\hat{j}-3 \hat{k})+t(-\hat{i}+4 \hat{k})\) meets the plane \(\vec{r} \cdot(\hat{i}+\hat{j}-\hat{k})\) are
(a) (2, 1, 0)
(b) (7, -1, -7)
(c) (1, 2, -6)
(c) (5, -1, 1)
Solution:
(d) (5, -1, 1)
Hint:
Cartesian equation of the line
\(\frac{x-6}{-1}=\frac{y+1}{0}+\frac{z+3}{4}\) = λ
(-λ + 6, -1, 4λ – 3)
This meets the plane x + y – z = 3
-λ + 6 – 1 – 41 + 3 = 3 ⇒ -5λ = -5
λ = 1
The required point (5, -1, 1).
Question 19.
Distance from the origin to the plane 3x – 6y + 2z + 7 = 0 is ………………
(a) 0
(b) 1
(c) 2
(d) 3
Solution:
(b) 1
Hint:
Distance from the origin (0, 0, 0) to the plane
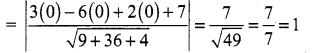
Question 20.
The distance between the planes x + 2y + 3z + 7 = 0 and 2x + 4y + 6z + 7 = 0 is ……………

Solution:
(a) \(\frac{\sqrt{7}}{2 \sqrt{2}}\)
Hint:
x + 2y + 3z + 1 = 0; 2x + 4y + 6z + 7 = 0
Multiplying 2 on both sides
2x + 4y + 6z + 14 = 0 .
a = 2, b = 4, c = 6, d1 = 14, d2 = ?
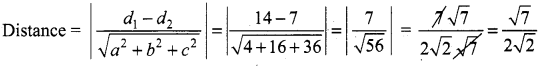
![]()
Question 21.
If the direction cosines of a line are \(\frac{1}{c}, \frac{1}{c}, \frac{1}{c}\), then ……………….
(a) c = ±3
(b) c = ± \(\sqrt{3}\)
(c) c > 0
(d) 0 < c < 1
Solution:
(b) c = ± \(\sqrt{3}\)
Hint:
We know that sum of the squares of direction cosines = 1
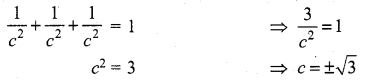
Question 22.
The vector equation \(\vec{r}=(\hat{i}-2 \hat{j}-\hat{k})+t(6 \vec{j}-\hat{k})\) represents a straight line passing through the points ……………. (a) (0, 6, -1) and (1, -2, -1) (b) (0, 6, -1) and (-1, -4, -2) (c) (1, -2, -1) and (1, 4, -2) (d) (1, -2, -1) and (0, -6, 1)
Solution:
(c) (1, -2, -1) and (1, 4, -2)
Hint:
The required vector equation is \(\vec{r}=\vec{a}+t(\vec{b}-\vec{a})\)
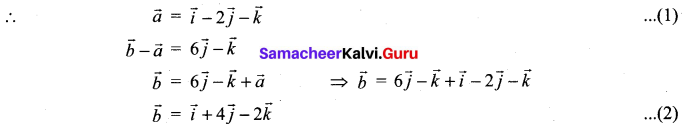
From (1) and (2) The points are (1, -2, -1) and (1, 4, -2)
Question 23.
If the distance of the point (1, 1, 1) from the origin is half of its distance from the plane x + y + z + k= 0, then the values of k are ………….. (a) ±3 (b) ±6 (c) -3, 9 (d) 3, -9
Solution:
(d) 3, -9
Hint:
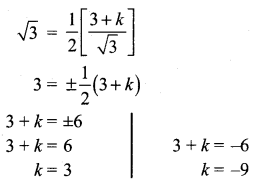
Question 24.
If the planes \(\vec{r} \cdot(2 \hat{i}-\lambda \hat{j}+\hat{k})=3 \text { and } \vec{r} \cdot(4 \hat{i}+\hat{j}-\mu \hat{k})\) = 5 are parallel, then the value of λ and µ are ……………
Solution:
(c) \(-\frac{1}{2}\), -2
Hint:
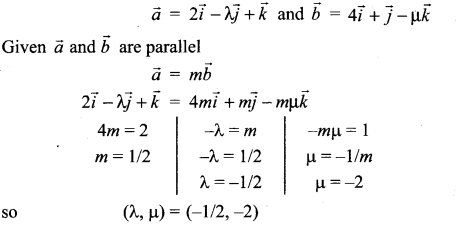
Question 25.
If the length of the perpendicular from the origin to the plane 2x + 3y + λz = 1, λ > 0 is \(-\frac{1}{5}\), then the value of λ is …………..
(a) \(2 \sqrt{3}\)
(b) \(3 \sqrt{2}\)
(c) 0
(d) 1
Solution:
(a) \(2 \sqrt{3}\)
Hint:
Given length of perpendicular from origin to the plane = \(-\frac{1}{5}\)
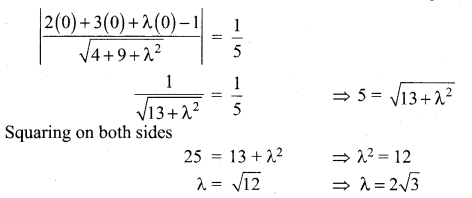
Samacheer Kalvi 12th Maths Solutions Chapter 6 Applications of Vector Algebra Ex 6.10 Additional Problems
Question 1.
![]()
(a) 6
(b) 10
(c) 12
(d) 24
Solution:
(c) 12
Hint:
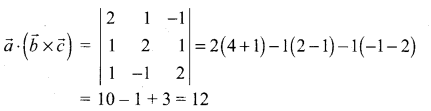
Question 2.
![]()
(a) only x
(b) only y
(c) Neither x nor y
(d) Both x and y
Solution:
(c) Neither x nor y
Hint:
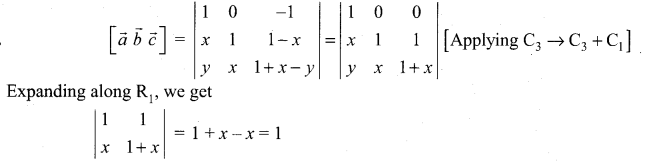
Question 3.
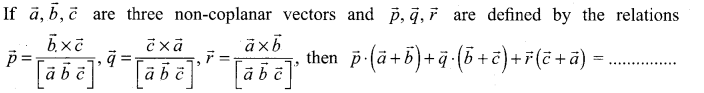
(a) 0
(b) 1
(c) 2
(d) 3
Solution:
(b) 3
Hint:
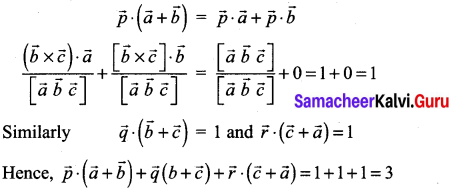
Question 4.
The value of ![]() = ………………
= ………………
(a) 1
(b) 3
(c) -3
(d) 0
Solution:
(b) 3
Hint:
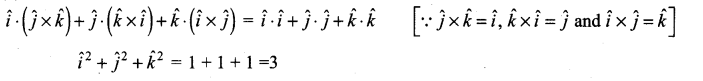
![]()
Question 5.
Let a, b, c be distinct non-negative numbers. If the vectors ![]() lie in a plane, then c is ……………..
lie in a plane, then c is ……………..
(a) the A.M. of a and b
(b) the G.M. of a and b
(c) the H.M. of a and b
(d) equal to zero.
Solution:
(b) the G.M. of a and b
Hint:

Question 6.
The value of \(\hat{i} \cdot(\hat{j} \times \hat{k})+(\hat{i} \times \hat{k}) \cdot \hat{j}\) ………….
(a) 1
(b) -1
(c) 0
(d) \(\hat{j}\)
Solution:
(c) 0
Hint:

Question 7.
The value of \((\hat{i}-\hat{j}, \hat{j}-\hat{k}, \hat{k}-\hat{i})\) is …………..
(a) 0
(b) 1
(c) 2
(d) 3
Solution:
(a) 0
Hint:
![]()
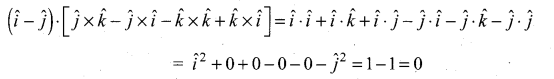
Question 8.
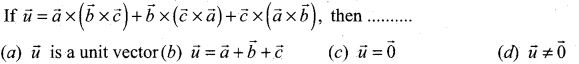
Solution:
(c) \(\vec{u}=\overrightarrow{0}\)
Hint:
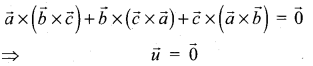
Question 9.
The area of the parallelogram having a diagonal \(3 \vec{i}+\vec{j}-\vec{k}\) and a side \(\vec{i}-3 \vec{j}+4 \vec{k}\) is ………………

Solution:
(d) \(3 \sqrt{30}\)
Solution:
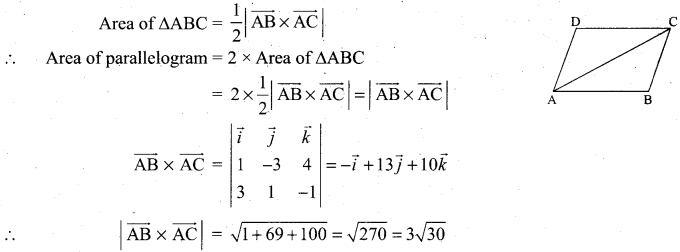
![]()
Question 10.
If ![]() , then ……………….
, then ……………….
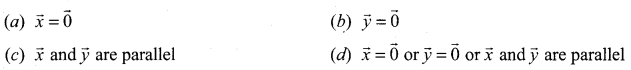
Solution:
(d) \(\vec{x}=\overrightarrow{0} \text { or } \vec{y}=\overrightarrow{0} \text { or } \vec{x} \text { and } \vec{y}\) are parallel
Hint:
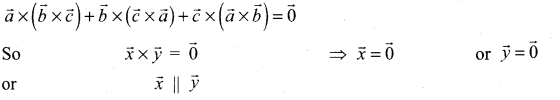
Question 11.
If \(\overrightarrow{\mathrm{PR}}=2 \vec{i}+\vec{j}+\vec{k}, \overrightarrow{\mathrm{Question}}=-\vec{i}+3 \vec{j}+2 \vec{k}\), then the area of the quadrilateral PQRS is ………………..

Solution:
(c) \(\frac{5 \sqrt{3}}{2}\)
Hint:

Question 12.

Solution:
(c) \(\vec{c}\) parallel to \(\vec{a}\)
Hint: