Samacheer Kalvi 12th Maths Solutions Chapter 5 Two Dimensional Analytical Geometry – II Ex 5.6

You can Download Samacheer Kalvi 12th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 5 Two Dimensional Analytical Geometry – II Ex 5.6

Choose the correct or the most suitable answer from the given four alternatives.
Question 1.
The equation of the circle passing through (1,5) and (4, 1) and touching y-axis is x² + y² – 5x – 6y + 9 + λ (4x + 3y – 19) = 0 where λ is equal to …………
(a) 0, \(-\frac{40}{9}\)
(b) 0
(c) \(\frac{40}{9}\)
(d) \(-\frac{40}{9}\)
Solution:
(a) 0, \(-\frac{40}{9}\)
Hint:
x² + y² – 5x – 6y + 9 + λ (4x + 3y -19) = 0
ie., x² + y² + x(4λ – 5) + y(3λ – 6) + 9 — 19λ = 0
Since it touches y axis x = 0
⇒ y² + y(3λ – 6) + 9 – 19λ = 0
It is a quadratic in y ,
Since the circle touches y axis the roots must be equal ⇒ b² – 4ac = 0
ie.,(3λ – 6)² – 4(1) (9 – 19λ) = 0
Solving we get λ = o or \(-\frac{40}{9}\)

Question 2.
The eccentricity of the hyperbola whose latus rectum is 8 and conjugate axis is equal to half the distance between the foci is ………..

Solution:
(c) \(\frac{2}{\sqrt{3}}\)
Hint:
Given \(\frac{2 b^{2}}{a}\) = 8 and 2b = ae

Question 3.
The circle x² + y² = 4x + 8y + 5 intersects the line 3x – 4y = m at two distinct points if …………..
(a) 15 < m < 65
(b) 35 < m < 85
(c) -85 < m < -35
(d) -35 < m < 15
Solution:
(d) -35 < m < 15
Hint:
x² + y² – 4x – 8y – 5 =0
3x – 4y = m Solving (1) and (2) we get
from (2) ⇒ 3x = 4y + m
x = \(\frac{4 y+m}{3}\)
Substituting x value in (1) we get
\(\left(\frac{4 y+m}{3}\right)^{2}\) + y² – \(4\left(\frac{4 y+m}{3}\right)\) – 8y – 5 = 0
It is a quadratic in y and given that the roots are distinct
⇒ b² – 4ac > 0
On simplifying we get
⇒ – 9m² – 18w + 4725 >0 ⇒ m² + 20m – 525 < 0
⇒ (m + 35) (m – 15) ≤ 0 ⇒ m lies between -35 and 15 ie„ – 35 < m < 15

Question 4.
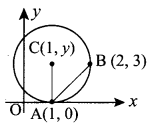
The length of the diameter of the circle which touches the x -axis at the point (1,0) and passes through the point (2, 3) …………

Solution:
(c) \(\frac{10}{3}\)
Hint:
Since radius is ⊥ r to tangent it passes through the centre (1, y)
AC = CB = radius
AC² = CB² ⇒ y² = 1 + (y – 3)²
6y = 10 ⇒ y = \(\frac{5}{3}\)
Diameter 2y = \(\frac{10}{3}\)

Question 5.
The radius of the circle 3x² + by² + 4bx – 6by + b² = 0 is ……………
(a) 1
(b) 3
(c) \(\sqrt{10}\)
(d) \(\sqrt{11}\)
Solution:
(c) \(\sqrt{10}\)
Hint:
Here b = 3
3x² + 3y² + 12x- 18y + 9 = 0
(÷ 3) zz> x² + y² + 4x – 6y + 3 = 0
Comparing with general form
g = 2,f = -3, c = 3
∴ radius = \(\sqrt{g^{2}+f^{2}-c}=\sqrt{4+9-3}=\sqrt{10}\)

Question 6.
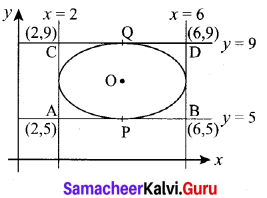
The centre of the circle inscribed in a square formed by the lines x² – 8x – 12 = 0 and y² – 14y + 45 = 0 is ………..
(a) (4, 7)
(b) (7, 4)
(c) (9, 4)
(d) (4, 9)

Solution:
(a) (4, 7)
Hint:
(x – 6) (x – 2) = 0 ⇒ x = 2 or 6
(y – 9) (y – 5) = 0 ⇒ y = 5 or 9

Question 7.
The equation of the normal to the circle x² + y² – 2x – 2y + 1 = 0 which is parallel to the line 2x + 4y = 3 is …………..
(a) x + 2y = 3
(b) x + 2y + 3 = 3
(c) 2x + 4y + 3 = 0
(d) x – 2y + 3 = 0
Solution:
(a) x + 2y = 3
Hint:
Centre of the circle = (1, 1) and radius = r = 1
Normal is parallel to 2x + 4y = 3
So equation of normal will be the form 2x + 4y = k
It passes throug the centre (1, 1) ⇒ 2 + 4 = 6 = k
So equation of the normal is x + 4y = 6
(÷ by 2) x + 2y = 3

Question 8.
If P(x, y) be any point on 16x² + 25y² = 400 with foci F₁(3, 0) and F₂(- 3, 0) then PF₁ + PF₂ is
(a) 8
(b) 6
(c) 10
(d) 12
Solution:
(c) 10
Hint:
F₁P + F₂P = 2a
Here the equation is 16x² + 25y² = 400
(÷ by 400) ⇒ \(\frac{16 x^{2}}{400}+\frac{25 y^{2}}{400}\) = 1 ⇒ \(\frac{x^{2}}{25}+\frac{y^{2}}{16}\) = 1
a² = 25 => a = 5
∴ 2a = 10

Question 9.
The radius of the circle passing through the point (6, 2) two of whose diameter are x + y = 6 and x + 2y = 4 is …………..
(a) 10
(b) \(2 \sqrt{5}\)
(c) 6
(d) 4
Solution:
(b) \(2 \sqrt{5}\)
Hint:
The point of intersection of the diameters is the centre.
Now solving x + y = 6 …………. (1)
x + 2y = 4 ………….. (2)
(1) – (2) ⇒ -y = 2 ⇒ y = -2
Substituting y = -6 in (1)
x – 2 = 6 ⇒ x = 8
Centre = (8, -2)
The circle passes through (6, 2)
∴ radius = \(\sqrt{(8-6)^{2}+(-2-2)^{2}}=\sqrt{4+16}\)
= \(\sqrt{20}=\sqrt{4 \times 5}=2 \sqrt{5}\)

Question 10.
The area of quadrilateral formed with foci of the hyperbolas \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}\) = 1 and \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}\) = -1 is ……………
(a) 4(a² + b²)
(b) 2(a² + b²)
(c) a² + b²
(d) \(\frac{1}{2}\)(a² + b²)
Solution:
(b) 2(a² + b²)
Hint:
The foci are (± ae, 0) and (0, ± ae)

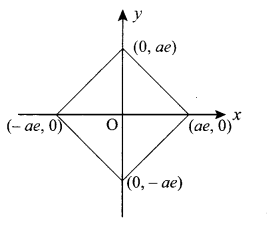
The above diagram is a rhombus.
Its area = \(\frac{1}{2}\)d₁d₂
= \(\frac{1}{2}\) (2ae) (2ae) = 2a² e²
But we know b² = a² (e² – 1)
i.e., b² = a² e² – a²
⇒ b² + a² = a² e²
So area = 2(a² + b²)

Question 11.
If the normals of the parabola y² = 4x drawn at the end points of its latus rectum are tangents to the circle (x – 3)² + (y + 2)² = r² , then the value of r² is ………………..
(a) 2
(b) 3
(c) 1
(d) 4
Solution:
(a) 2
Hint:
The normals are x ± y = 3
Distance from (3, -2) on both normal is r
(i.e.,) r = \(\left|\frac{3-2-3}{\sqrt{2}}\right|=\sqrt{2}\) ⇒ r² = 2

Question 12.
If x + y = k is a normal to the parabola y² = 12x, then the value of k is ……………
(a) 3
(b) -1
(c) 1
(d) 9
Solution:
(d) 9
Hint:
Slope of normal = -1 and Slope of tangent = -1
The condition for y = mx + c to be a tangent to the parabola
y² = 4ax is c = \(\frac{a}{m}\)
Here the parabola is y² = 12x ⇒ a = 3 and m = 1
∴ c = \(\frac{3}{1}\) = 3
∴ Equation of tangent is y = x + 3
Solving the parabola and tangent we get the points (3, 6) and (3,-6)
∴ k = -3 or k = 9

Question 13.
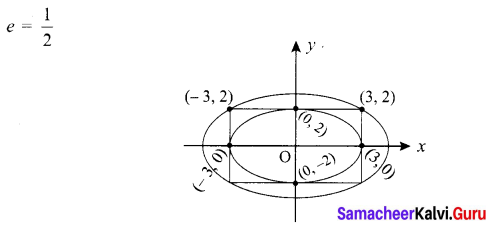
The ellipse E₁ : \(\frac{x^{2}}{9}+\frac{y^{2}}{4}\) = 1 is inscribed in a rectangle R whose sides are parallel to the coordinate axes. Another ellipse E₂ passing through the point (0, 4) circumscribes the rectangle R. The eccentricity of the ellipse is …………….

Solution:
(c) \(\frac{1}{2}\)
Hint:

Question 14.
Tangents are drawn to the hyperbola \(\frac{x^{2}}{9}-\frac{y^{2}}{4}\) = 1 parallel to the straight line 2x – y = 1. One of the points of contact of tangents on the hyperbola is ……………

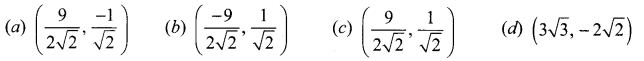
Solution:
(c) \(\left(\frac{9}{2 \sqrt{2}}, \frac{1}{\sqrt{2}}\right)\)
Hint:
The tangents are parallel to 2x – y = 1
So equation of tangents will be of the form
2x – y = k ⇒ y = 2x – k
Comparing this equation with y = mx + c we get m = 2 and c = -k
The given hyperbola is \(\frac{x^{2}}{9}-\frac{y^{2}}{4}\) = 1
⇒ a² = 9 and b² = 4
Now the condition for the line y = mx + c to be a tangent to

Question 15.
The equation of the circle passing through the foci of the ellipse \(\frac{x^{2}}{16}-\frac{y^{2}}{9}\) = 1 having centre at (0, 3) is ……………….
(a) x² + y² – 6y – 7 = 0
(b) x² + y² – 6y + 7 = 0
(c) x² + y² – 6y – 5 = 0
(d) x² + y² – 6y + 5 = 0
Solution:
(a) x² + y² – 6y – 7 = 0

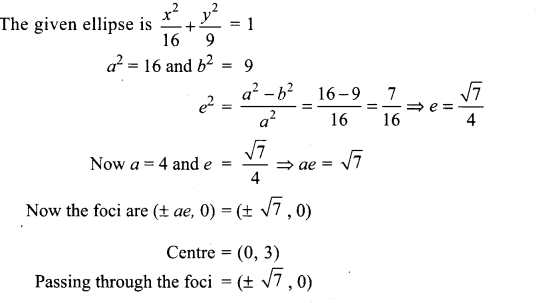
The distance between centre and foci = radius of the circle
ie., r = \(\sqrt{(0 \pm \sqrt{7})^{2}+(3-0)^{2}}=\sqrt{7+9}=\sqrt{16}\) = 4
Now Centre = (0, 3); r = 4
Equation of the circle is (x – 0)2 + (y -3)2 = 42
ie., x² + y² – 6y + 9 – 16 = 0
x² + y² – 6y – 7 = 0

Question 16.
Let C be the circle with centre at (1, 1) and radius = 1. If T is the circle centered at (0, y) passing through the origin and touching the circle C externally, then the radius of T is equal ……………..

Solution:
(d) \(\frac{1}{4}\)
Hint:
Equation of circle is x² + y² + 2gx + 2fy + c = 0
i.e., (1 + y²)² = (1 – y)² = 1
Solving we get y = \(\frac{1}{4}\)

Question 17.
Consider an ellipse whose centre is of the origin and its major axis is along x-axis. If its eccentricity is \(\frac{3}{5}\) and the distance between its foci is 6, then the area of the quadrilateral inscribed in the ellipse with diagonals as major and minor axis of the ellipse is ……………
(a) 8
(b) 32
(c) 80
(d) 40
Solution:
(d) 40
Hint:

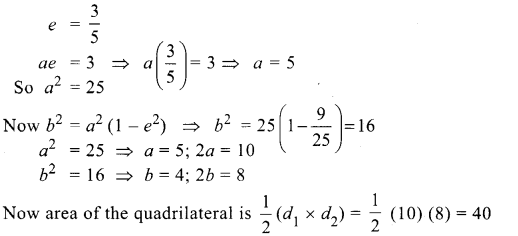
Question 18.
Area of the greatest rectangle inscribed in the ellipse \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}\) = 1 is …………….
(a) 2ab
(b) ab
(c) \(\sqrt{a b}\)
(d) \(\frac{a}{b}\)
Solution:
(a) 2ab
Hint:
Area of the greatest rectangle is (\(\sqrt{2}\) a) (\(\sqrt{2}\) b) = 2ab

Question 19.
An ellipse has OB as semi minor axes, F and F’ its foci and the angle FBF’ is a right angle. Then the eccentricity of the ellipse is …………..

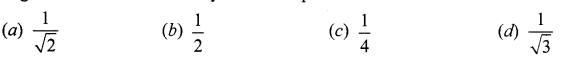
Solution:
(a) \(\frac{1}{\sqrt{2}}\)
Hint:

Question 20.
The eccentricity of the ellipse (x – 3)² + (y – 4)² = \(\frac{y^{2}}{9}\) is ……………

Solution:
(b) \(\frac{1}{3}\)
Hint:
The given equation is of the form FP² = e²PM²
i.e., (x – 3)² + (y – 4)² = \(\frac{1}{9}\)(y²)
⇒ e² = \(\frac{1}{9}\) ⇒ e = \(\frac{1}{3}\)

Question 21.
If the two tangents drawn from a point P to the parabola y² = 4x are at right angles then the locus of P is ………………….
(a) 2x + 1 = 0
(b) x = -1
(c) 2x – 1 = 0
(d) x = 1
Solution:
(b) x = -1
Hint:
When the tangents at drawns from a point on the directrix are at right angles.
So equation of directrix to y² = 4x is x = -1

Question 22.
The circle passing through (1, -2) and touching the axis of x at (3, 0) passing through the point …………..
(a) (-5, 2)
(b) (2, -5)
(c) (5, -2)
(d) (-2, 5)
Solution:
(c) (5, -2)
Hint:

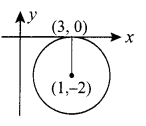
Let the centre be (3, h)
r = k
Equation of the circle is
(x – 3)² + (y – h)² = r² = (k)²
It passes through (1, -2) ⇒ k² = 8
Substituting (5, -2) the equation satisfies.

Question 23.
The locus of a point whose distance from (-2, 0) is \(\frac{2}{3}\) times its distance from the line x = \(\frac{-9}{2}\) is ……….
(a) a parabola
(b) a hyperbola
(c) an ellipse
(d) a circle
Solution:
(c) an ellipse
Hint:
Here e = \(\frac{2}{3}\) < 1
So the conic is an ellipse

Question 24.
The values of m for which the line y = mx + 2\(\sqrt{5}\) touches the hyperbola 16x² – 9y² = 144 are the roots of x² – (a + b)x -4 = 0, then the value of (a + b) is
(a) 2
(b) 4
(c) 0
(d) -2
Solution:
(c) 0
Hint:

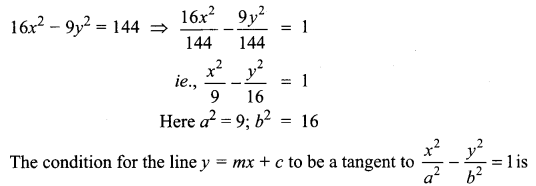
c² = a² m² – b²
Here the given line is y = mx + 2 \(\sqrt{5}\)
⇒ m = m and c = 2\(\sqrt{5}\)
The condition is c² = a²m² – b²
ie., (2\(\sqrt{5}\))²= 9(m²)- 16
⇒ 9m² = 20 + 16 = 36 ⇒ m² = 4
i.e., m = ± 2
a = 2, b = -2 (say)
So a + b = 2 – 2 = 0

Question 25.
If the coordinates at one end of a diameter of the circle x² + y² – 8x – 4y + c = 0 are (11, 2), the coordinates of the other end are ……………
(a) (-5, 2)
(b) (-3, 2)
(c) (5, -2)
(d) (-2, 5)
Solution:
(b) (-3, 2)
Hint:

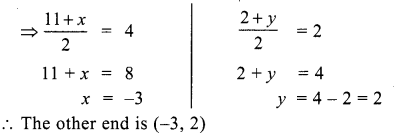
Samacheer Kalvi 12th Maths Solutions Chapter 5 Two Dimensional Analytical Geometry – II Ex 5.6 Additional Problems

Choose the most appropriate answer:
Question 1.
The parabola y² = 4ax passes through the point (2, -6), the the length of its latus rectum is …………..
(a) 9
(b) 16
(c) 18
(d) 6
Solution:
(c) 18
Hint:
The given parabola is y² = 4ax
Since it passes through (2, -6)
∴ (-6)² = 4a(2)
⇒ 36 = 8a a = \(\frac{36}{8}=\frac{9}{2}\)
Length of the latus rectum = 4a = \(4\left(\frac{9}{2}\right)\) = 18

Question 2.
The vertex of the parabola x² + 12x – 9y = 0 is …………
(a) (6, -1)
(b) (-6, 4)
(c) (6, 4)
(d) (-6, -4)
Solution:
(d) (-6, -4)
Hint:
Given parabola is x² + 12x – 9y = 0
⇒ (x² + 12x + 36) – 36 – 9y = 0
⇒ (x + 6)² = 9y + 36 ⇒ (x + 6)² = 9 (y + 4)
∴ Vertex = (-6, -4)

Question 3.
The length of the major axis of an ellipse is three times the length of minor axis, its eccentricity is ……………

Solution:
(d) \(\frac{2 \sqrt{2}}{3}\)
Hint:
Length of major axis = 2a and Length of minor axis = 2b
2a = 3(2b) ⇒ a = 3b

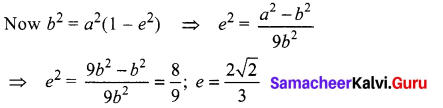
Question 4.
The eccentricity of the ellipse 9x² + 4y² = 36 is …………..

Solution:
(d) \(\frac{\sqrt{5}}{3}\)
Hint:
Given equation of the ellipse 9x² + 4y² = 36
On dividing both the sides by 36, we get

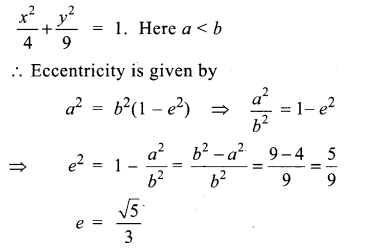
Question 5.
S and T are the foci of the ellipse \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}\) = 1 and B is an end of the minor axis. If STB is an equilateral triangle, the eccentricity of the ellipse is …………..

Solution:
(c) \(\frac{1}{2}\)
Hint:

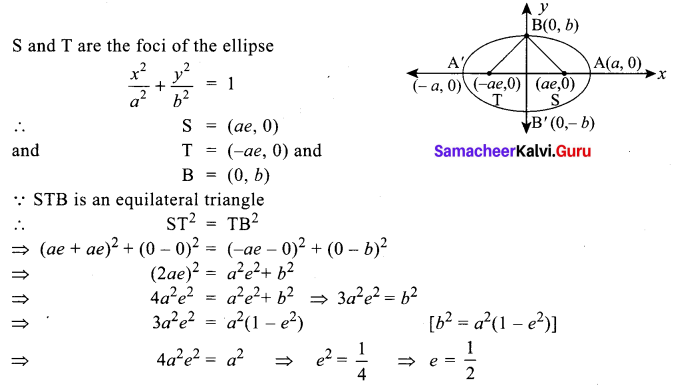
Question 6.
The sum of the focal distances from any point of the ellipse 9x² + 16y² = 144 is …………….
(a) 32
(b) 18
(c) 16
(d) 8
Solution:
(d) 8
Hint:
We have, 9x² + 16y² = 144
⇒ \(\frac{x^{2}}{16}+\frac{y^{2}}{9}\) = 1 (Dividing both sides by 144)
Here a² = 16, b² = 9 ⇒ a = 4, b = 3
Length of major axis = 2a = 2(4) = 8
Since the sum of the focal distances from any point on the ellipse is equal to its major axis
∴ Required sum = 8

Question 7.
If the eccentricities of two ellipse \(\frac{x^{2}}{169}+\frac{y^{2}}{25}\) = 1 and \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}\) = 1 are equal then \(\frac{a}{b}\) = ………………

Solution:
(c) \(\frac{13}{5}\)
Hint:

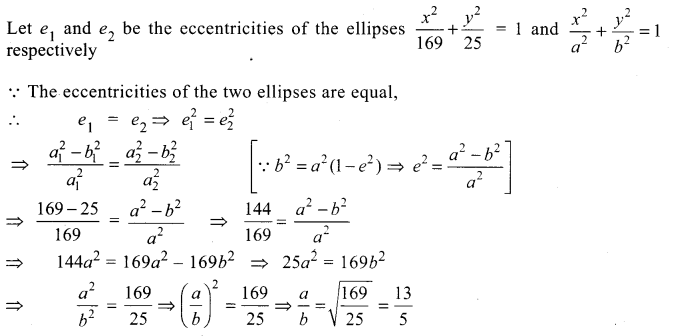
Question 8.
Equation of the hyperbola, whose eccentricity \(\frac{3}{2}\) and foci at (±2, 0) is ……………

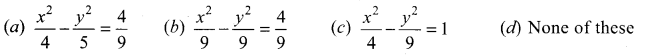
Solution:
(a) \(\frac{x^{2}}{4}-\frac{y^{2}}{5}=\frac{4}{9}\)
Hint:
Eccentricity e = \(\frac{c}{a}=\frac{3}{2}\)
Foci are (± c, 0) = (± 2, 0) (Given c = 2)

Question 9.
If e₁ is the eccentricity of the ellipse \(\frac{x^{2}}{25}+\frac{y^{2}}{9}\) = 1 and if e₂ is the eccentricity of the hyperbola 9x² – 16y² = 144, then e₁e₂ is …………….
(a) \(\frac{16}{25}\)
(b) 1
(c) Greater than 1
(d) Less than \(\frac{1}{2}\)
Solution:
(b) 1
Hint:

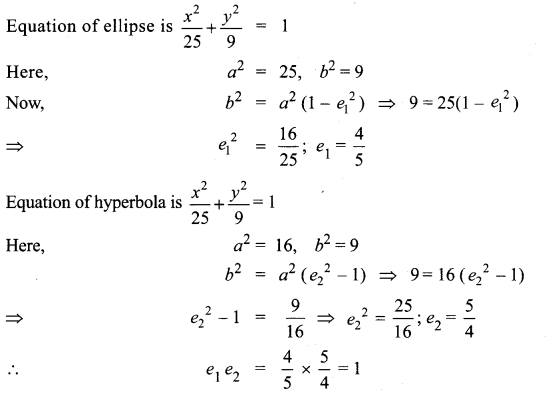
Question 10.
The point of intersection of the tangents at t₁ = t and t₂ = 3 t to the parabola y² = 8x is ………….
(a) (6t², 8t)
(b) (8t, 6t²)
(c) (t², 4t)
(d) (4t, t²)
Solution:
(a) (6t², 8t)
Hint:
Point of intersection of the tangents at t₁ and t₂ to y² = 4ax is [a t₁ t₂, a(t₁ + t₂)]
Here, t₁ = t, t₂ = 3t, a = latex]\frac{8}{4}[/latex] = 2
So a t₁ t₂ = 2(t) (3t) = 6t²
a(t₁ + t₂) = 2(t + 3t) = 8t
∴ Point = (6t², 8t²)