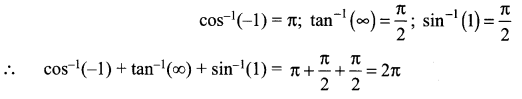You can Download Samacheer Kalvi 12th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 4 Inverse Trigonometric Functions Ex 4.6
Choose the correct or the most suitable answer from the given four alternatives.
Question 1.
The value of sin-1(cos x), 0 ≤ x ≤ π is …………
(a) π – x
(b) x – \(\frac{\pi}{2}\)
(c) \(\frac{\pi}{2}\) – x
(d) π – x
Solution:
(c) \(\frac{\pi}{2}\) – x
Hint:
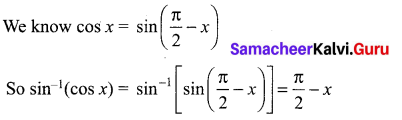
Question 2.
If sin-1 + sin-1 y = \(\frac{2 \pi}{3}\); then cos-1x + cos-1y is equal to ………….
(a) \(\frac{2 \pi}{3}\)
(b) \(\frac{\pi}{3}\)
(c) \(\frac{\pi}{6}\)
(d) π
Solution:
(b) \(\frac{\pi}{3}\)
Hint:

![]()
Question 3.
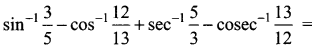 ……………
……………
(a) 2π
(b) π
(c) 0
(d) tan-1\(\frac{12}{65}\)
Solution:
(c) 0
Hint:
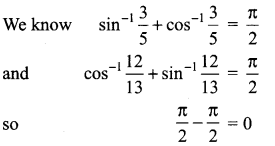
Question 4.
If sin-1x = 2 sin-1 α has a solution, then ……………

Solution:
(a) |α| ≤ \(\frac{1}{\sqrt{2}}\)
Hint:
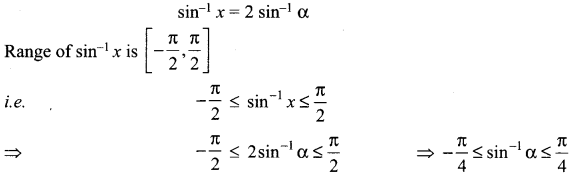
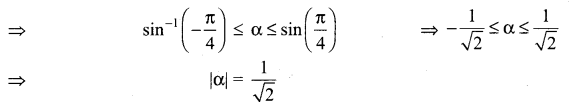
Question 5.
sin-1 (cos x) = \(\frac{\pi}{2}\) – x is valid for ……………..
(a) -π ≤ x ≤ 0
(b) 0 ≤ x ≤ π
(c) \(-\frac{\pi}{2}\) ≤ x ≤ \(\frac{\pi}{2}\)
(d) \(-\frac{\pi}{4}\) ≤ x ≤ \(\frac{3 \pi}{4}\)
Solution:
(b) 0 ≤ x ≤ π
Question 6.
If sin-1 x + sin-1 y + sin-1 z = \(\frac{3 \pi}{2}\), the value of x2017 + y2018 + z2019 – \(\frac{9}{x^{101}+y^{101}+z^{101}}\) is ……………….
(a) 0
(b) 1
(c) 2
(d) 3
Solution:
(a) 0
Hint:
The maximum value of sin-1 x is \(\frac{\pi}{2}\) and sin-1 1 = \(\frac{\pi}{2}\)
Here it is given that
sin-1 x + sin-1 y + sin-1 z = \(\frac{3 \pi}{2}\)
⇒ x = y = z = 1
and so 1 + 1 + 1 – \(\frac{9}{1+1+1}\) = 3 – 3 = 0
Question 7.
If cot-1 x = \(\frac{2 \pi}{5}\) for some x ∈ R, the value of tan-1 x is …………
(a) \(-\frac{\pi}{10}\)
(b) \(\frac{\pi}{5}\)
(c) \(\frac{\pi}{10}\)
(d) \(-\frac{\pi}{5}\)
Solution:
(c) \(\frac{\pi}{10}\)
Hint:

Question 8.
The domain of the function defined by f(x) = sin-1 \(\sqrt{x-1}\) is …………….
(a) [1, 2]
(b) [-1, 1]
(c) [0, 1]
(d) [-1, 0]
Solution:
(a) [1, 2]
Hint:
The domain for sin-1 x is [0, 1]
So \(\sqrt{x-1}\) = 0 ⇒ x – 1 = 0 ⇒ x = 1
\(\sqrt{x-1}\) = 1 ⇒ x – 1 = 0 ⇒ x = 2
∴ The domain is [1, 2]
![]()
Question 9.
If x = \(\frac{1}{5}\), the value of cos(cos-1 x + 2 sin-1 x) is …………….

Solution:
(d) \(-\frac{1}{5}\)
Hint:
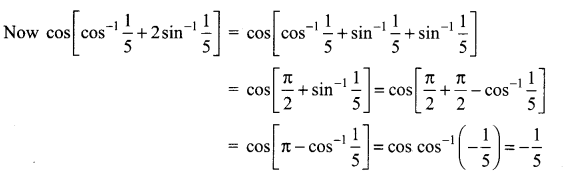
Question 10.
\(\tan ^{-1}\left(\frac{1}{4}\right)+\tan ^{-1}\left(\frac{2}{9}\right)\) is equal to …………

Solution:
(d) tan-1\(\frac{1}{2}\)
Hint:
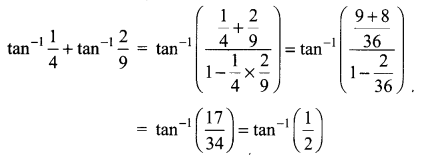
Question 11.
If the function f(x) = sin-1(x2 – 3), then x belongs to …………..
(a) [1, -1]
(b) [\(\sqrt{2}\), 2]
(c) \([-2,-\sqrt{2}] \cup[\sqrt{2}, 2]\)
(d) \([-2,-\sqrt{2}] \cap[\sqrt{2}, 2]\)
Solution:
(c) \([-2,-\sqrt{2}] \cup[\sqrt{2}, 2]\)
Hint:
f(x) = sin-1(x2 – 3)
Domain of sin-1 (x) is [-1, 1]
⇒ -1 ≤ x2 – 3 ≤ 1 ⇒ 2 ≤ x2 ≤ 4
⇒ \(\sqrt{2}\) ≤ x ≤ 2 ⇒ \(\sqrt{2}\) ≤ |x| ≤ 2
x ∈ \([-2,-\sqrt{2}] \cup[\sqrt{2}, 2]\)
Question 12.
If cot-1 2 and cot-1 3 are two angles of a triangle, then the third angle is …………..

Solution:
(b) \(\frac{3 \pi}{4}\)
Hint:

Question 13.
\(\sin ^{-1}\left(\tan \frac{\pi}{4}\right)-\sin ^{-1}(\sqrt{\frac{3}{x}})=\frac{\pi}{6}\). Then x is a root of the equation …………..
(a) x2 – x – 6 = 0
(b) x2 – x – 12 = 0
(c) x2 + x – 12 = 0
(d) x2 + x – 6 = 0
Solution:
(b) x2 – x – 12 = 0
Hint:
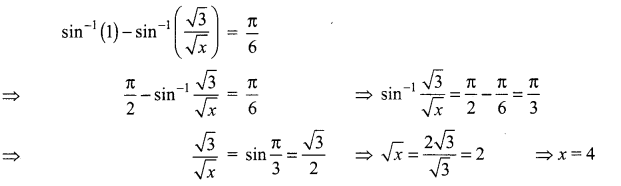
Question 14.
sin-1(2 cos2 x – 1) + cos-1(1 – 2 sin2 x) = ……………
![]()
Solution:
(a) \(\frac{\pi}{2}\)
Hint:
2 cos2x – 1 = cos 2x
1 – 2 sin2 x = cos 2x
∴ sin-1 x(cos 2x) + cos-1(cos 2x) = \(\frac{\pi}{2}\) (∵ sin-1 x + cos-1 x = \(\frac{\pi}{2}\))
Question 15.
If \(\cot ^{-1}(\sqrt{\sin \alpha})+\tan ^{-1}(\sqrt{\sin \alpha})\) = u, then cos 2u is equal to …………..
(a) tan2 α
(b) 0
(c) -1
(d) tan 2α
Solution:
(c) -1
Hint:
cot-1 x + tan-1 x = \(\frac{\pi}{2}\) ⇒ u = \(\frac{\pi}{2}\) so 2u = π
∴ cos 2u = cos π = -1
Question 16.
If |x| ≤ 1, then 2tan-1 x – sin-1 \(\frac{2 x}{1+x^{2}}\) is equal to ………….
(a) tan-1 x
(b) sin-1 x
(c) 0
(d) π
Solution:
(c) 0
Hint:
Let x = tan θ so \(\frac{2 x}{1+x^{2}}\) = sin 2θ.
Now 2 tan-1(tanθ) – sin-1(sin 2θ) = 2θ – 2θ = 0
Question 17.
The equation tan-1 x – cot-1 x = tan-1 \(\left(\frac{1}{\sqrt{3}}\right)\) has …………..
(a) no solution
(b) unique solution
(c) two solutions
(d) infinite number of solutions
Solution:
(b) unique solution
Hint:

![]()
Question 18.
If sin-1 x + cot-1 \(\left(\frac{1}{2}\right)=\frac{\pi}{2}\), then x is equal to …………

Solution:
(b) \(\frac{1}{\sqrt{5}}\)
Hint:
sin-1 x + cot-1 \(\left(\frac{1}{2}\right)=\frac{\pi}{2}\)
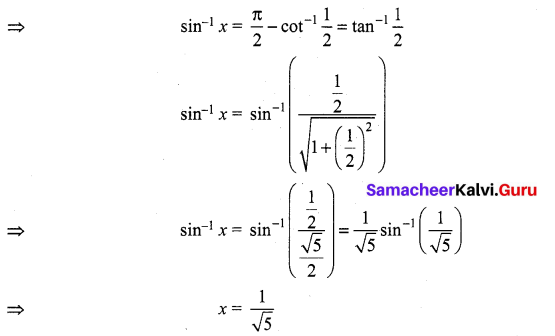
Question 19.
If sin-1\(\frac{x}{5}\) + cosec-1\(\frac{5}{4}\) = \(\frac{\pi}{2}\), then the value of x is ………
(a) 4
(b) 5
(c) 2
(d) 3
Solution:
(d) 3
Hint:

Question 20.
sin(tan-1), |x| < 1 is equal to ………….

Solution:
(d) \(\frac{x}{\sqrt{1+x^{2}}}\)
Hint:
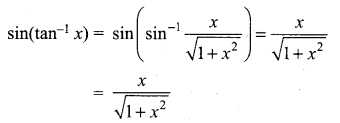
Samacheer Kalvi 12th Maths Solutions Chapter 4 Inverse Trigonometric Functions Ex 4.6 Additional Questions
Question 1.
Find the principal value of 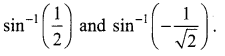
Solution:
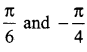
Question 2.
Find the principal value of 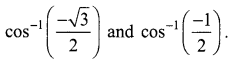
Solution:
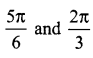
Question 3.
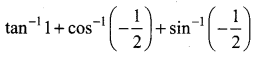
Solution:
![]()
Question 4.
Evaluate
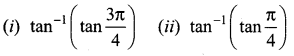
Solution:
![]()
![]()
Question 5.
Evaluate
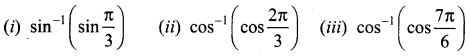
Solution:
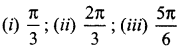
Question 6.
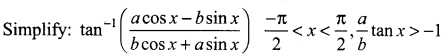
Question 7.

Solution:
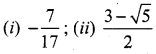
Question 8.
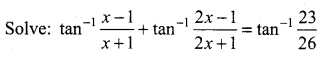
Solution:
x = \(\frac{1}{6}\)
Question 9.
Find the values of each of the following:
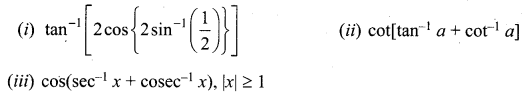
Solution:
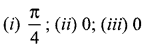
Question 10.
Solve for x:

Solution:
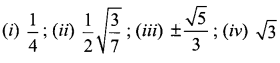
Question 11.
Prove:

![]()
Question 12.
Evaluate: sin(tan-1 x + cot-1 x)
Question 13.
The value of sin-1(1) + sin-1(0) is …….
![]()
Solution:
(a) \(\frac{\pi}{2}\)
Hint:
![]()
Question 14.
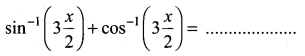

Solution:
(d) \(\frac{\pi}{2}\)
Hint:
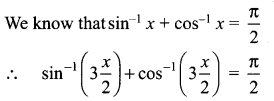
Question 15.
tan-1x + cot-1x = ……..
(a) 1
(b) – π
(c) \(\frac{\pi}{2}\)
(d) π
Solution:
(c) \(\frac{\pi}{2}\)
Hint:
![]()
Question 16.
![]()

Solution:
(a) \(\frac{-\pi}{2}\)
Hint:
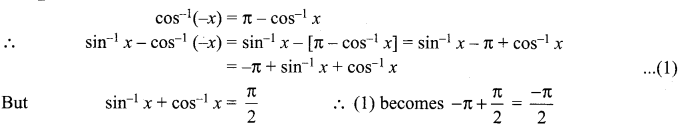
Question 17.
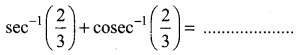
![]()
Solution:
(b) \(\frac{\pi}{2}\)
Hint:
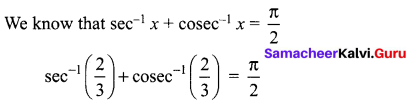
![]()
Question 18.
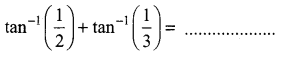
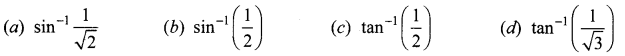
Solution:
(a) \(\sin ^{-1} \frac{1}{\sqrt{2}}\)
Hint:
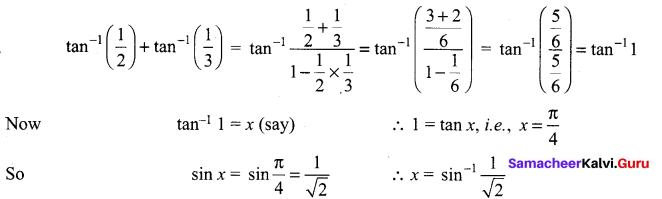
Question 19.
![]()
![]()
Solution:
(d) 2π
Hint:
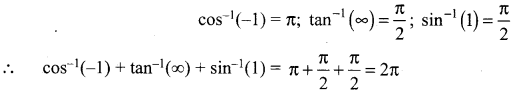
Question 20.
![]()
![]()
Solution:
(c) 2π
Hint: