You can Download Samacheer Kalvi 12th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 2 Complex Numbers Ex 2.2
Question 1.
Evaluate the following if z = 5 – 2i and w = -1 + 3i
(i) z + w
(ii) z – iw
(iii) 2z + 3w
(iv) zw
(v) z2 + 2zw+ w2
(vi) (z + w)2
Solution:
(i) z + w = (5 – 2i) + (-1 + 3i)
= 4 + i
(ii) z – iw= (5 – 2i) -i (-1 + 3i)
= 5 – 2i + i + 3i² (∵ i² = -1)
= 5 – 2i + i – 3(-1)
= 5 – 2i + i + 3
= 8 – i
(iii) 2z + 3w = 2 (5 – 2i) + 3 (- 1 +3i)
= 10 – 4i – 3 + 9i
= 7 + 5i
(iv) zw = (5 – 2i) (- 1 + 3i)
= -5 + 2i + 15i – 6i²
= -5 + 17i + 6
= 1 + 17i
(v) z2 + 2zw + w2
= (z + w)²
= (4 + i)²
= (4) + 2(4)(i) + (i)²
= 16 + 8i + i²
= 15 + 8i
(vi) (z + w)2 = z² + 2zw + w²
= (z + w)² = (4 + i)²
= 16 + 8i + i²
= 15 + 8i
![]()
Question 2.
Given the complex number z = 2 + 3i, represent the complex numbers in the Argand diagram.
(i) z, iz, and z + iz
(ii) z, -iz, and z – iz
Solution:
(i) z, iz and z + iz.
z = 2 + 3i
iz = i(2 + 3i) = -3 + 2i
z + iz = 2 + 3i – 3 + 2i = -1 + 5i
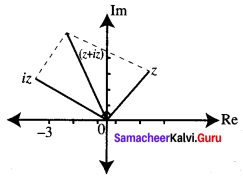
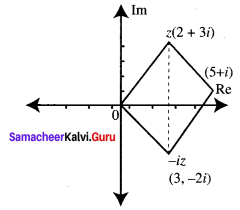
(ii) z = 2 + 3i
-iz = -i(2 + 3i)
= -2i – 3i2
= (3 – 2i)
z – iz = (2 + 3i) + (3 – 2i)
= 5 + i
Question 3.
Find the values of the real numbers x and y, if the complex numbers.
(3 – i) x – (2 – i) y + 2i + 5 and 2x + (-1 + 2i) y + 3 + 2i are equal
Solution:
Given that the complex numbers are equal
(3 – i) x -(2 – i) y + 3 + 2i + 5
= 2x + (-1 + 2i)y + 3 + 2i
3x – ix – 2y + iy + 2i +5
= 2x – y + 2iy + 3 + 2i
(3x – 2y + 5) + i(y – x + 2)
= (2x – y + 3) + i(2y + 2)
Equating real and imaginary parts separately
3x – 2y + 5 = 2x – y + 3
x – y = -2 ………. (1)
y – x + 2 = 2y +
-x – y = 0 ………. (2)
solving 1 and 2
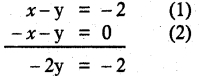
y = 1
Substituting y = 1 in (1)
x – 1 = -2
x = -2 + 1 = -1
values of x and y are -1, 1
![]()
Samacheer Kalvi 12th Maths Solutions Chapter 2 Complex Numbers Ex 2.2 Additional Problems
Question 1.
Find the real values of x and y, if
(i) (3x – 7) + 2 iy = -5y + (5 + x)i
(ii) (1 – i)x + (1 + i)y = 1 – 3i
(iii) (x + iy)(2 – 3i) = 4 + i
(iv) ![]()
Solution:
(i) We have (3x – 7) + 2 iy = 5y + (5 + x)i
⇒ 3x – 7 = 5y and 2y = 5 + x
⇒ 3x + 5y = 7 and x – 2y = -5
⇒ x = -1 y = 2
(ii) We have, (1 – i) x + (1 + i)y = 1 – 3i
⇒ (x + y) + i(-x + y) = 1 – 3i
⇒ x + y = 1
and -x + y = 3 [On equating real and imaginary parts]
⇒ x = 2 and y = -1

⇒ x + y – 2 = 0 and y – x = 10
⇒ x = -4 , y = 6.
![]()
Question 2.
Find the real values of x and y for which the complex numbers -3 + ix2y and x2 + y + 4i are conjugate of each other.
Solution:
Since -3 + ix2y and x2 + y + 4i are complex conjugates.
∴ -3 + ix2y = x2 + y + 4i ….. (i) and, x2 y = -4 …… (ii)
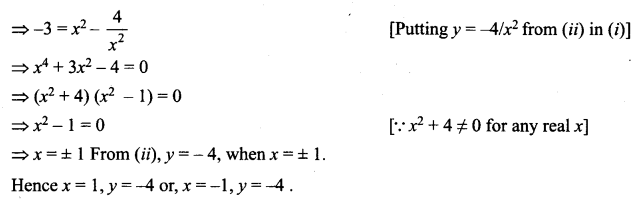
Question 3.
Given x = 2 – 3i and y = 4 + i
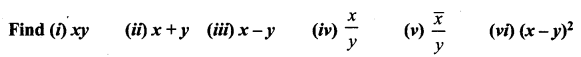
Solution:
Do it yourself