Students can Download Physics Chapter 5 Motion of System of Particles and Rigid Bodies Questions and Answers, Notes Pdf, Samacheer Kalvi 11th Physics Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 11th Physics Solutions Chapter 5 Motion of System of Particles and Rigid Bodies
Samacheer Kalvi 11th Physics Motion of System of Particles and Rigid Bodies Textual Questions Solved
Samacheer Kalvi 11th Physics Motion of System of Particles and Rigid Bodies Multiple Choice Questions
Question 1.
The center of mass of a system of particles does not depend upon,
(a) position of particles
(b) relative distance between particles
(c) masses of particles
(d) force acting on particle
Answer:
(d) force acting on particle
Question 2.
A couple produces, [AIPMT 1997, AIEEE 2004]
(a) pure rotation
(b) pure translation
(c) rotation and translation
(d) no motion [AIPMT 1997]
Answer:
(a) pure rotation
Question 3.
A particle is moving with a constant velocity along a line parallel to positive X – axis. The magnitude of its angular momentum with respect to the origin is –
(a) zero
(b) increasing with x
(c) decreasing with x
(d) remaining constant [IIT 2002]
Answer:
(d) remaining constant
Question 4.
A rope is wound around a hollow cylinder of mass 3 kg and radius 40 cm. What is the angular acceleration of the cylinder if the rope is pulled with a force 30 N?
(a) 0.25 rad s-2
(b) 25 rad s-2
(c) 5 m s-2
(d) 25 m s-2
[NEET 2017]
Answer:
(b) 25 rad s-2
Question 5.
A closed cylindrical container is partially filled with water. As the container rotates in a horizontal plane about a perpendicular bisector, its moment of inertia,
(a) increases
(b) decreases
(c) remains constant
(d) depends on direction of rotation. [IIT 1998]
Answer:
(a) increases
![]()
Use this kinetic energy calculator to help you find out the energy of an object in motion. This KE calculator makes use of the kinetic energy formula
Question 6.
A rigid body rotates with an angular momentum L. If its kinetic energy is halved, the angular momentum becomes,
(a) L
(b) L / 2
(c) 2 L
(d) L / 2 [AFMC 1998, AIPMT 2015]
Answer:
(d) L / 2
Question 7.
A particle undergoes uniform circular motion. The angular momentum of the particle remain conserved about –
(a) the center point of the circle.
(b) the point on the circumference of the circle
(c) any point inside the circle.
(d) any point outside the circle. [IIT 2003]
Answer:
(a) the center point of the circle.
Question 8.
When a mass is rotating in a plane about a fixed point, its angular momentum is directed along –
(a) a line perpendicular to the plane of rotation
(b) the line making an angle of 45° to the plane of rotation
(c) the radius
(d) tangent to the path [AIPMT 2012]
Answer:
(a) a line perpendicular to the plane of rotation
Question 9.
Two discs of same moment of inertia rotating about their regular axis passing through center and perpendicular to the plane of disc with angular velocities ω1 and ω1. They are brought in to contact face to face coinciding the axis of rotation. The expression for loss of energy during this process is-
(a) \(\frac {1}{4}\) I(ω1 – ω2)ω2
(b) I(ω1 – ω2)ω2
(c) \(\frac {1}{8}\) I(ω1 – ω2)ω2
(d) \(\frac {1}{2}\) I(ω1 – ω2)ω2
Answer:
(a) \(\frac {1}{4}\) I(ω1 – ω2)ω2
Question 10.
A disc of moment of inertia Ia is rotating in a horizontal plane about its symmetry axis with a constant angular speed to. Another disc initially at rest of moment of inertia Ib is dropped coaxially on to the rotating disc. Then, both the discs rotate with same constant angular speed. The loss of kinetic energy due to friction in this process is-
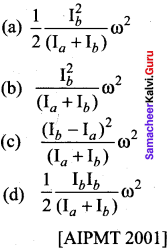
Answer:
![]()
![]()
Question 11.
The ratio of the acceleration for a solid sphere (mass m and radius R) rolling down an incline of angle 0 without slipping and slipping down the incline without rolling is –
(a) 5 : 7
(b) 2 : 3
(c) 2 : 5
(d) 7 : 5
[AIPMT 2014]
Answer:
(a) 5 : 7
Question 12.
From a disc of radius R a mass M, a circular hole of diameter R, whose rim passes through the center is cut. What is the moment of inertia of the remaining part of the disc about a perpendicular axis passing through it?
(a) 15MR2/32
(b) 13MR2/32
(c) 11MR2/32
(d) 9MR2/32 [NEET 2016]
Answer:
(b) 13MR2/32
Question 13.
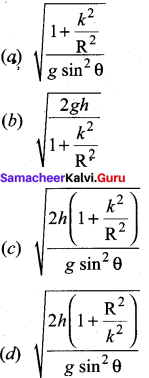
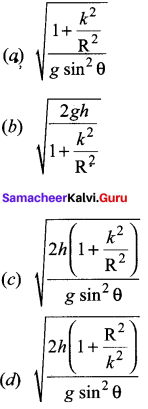
The speed of a solid sphere after rolling down from rest without sliding on an inclined plane of vertical height h is,
(a) \(\sqrt{\frac{4}{3} g h}\)
(b) \(\sqrt{\frac{10}{7} g h}\)
(c) \(\sqrt{2gh}\)
(d) \(\sqrt{\frac{1}{2} g h}\)
Answer:
(a) \(\sqrt{\frac{4}{3} g h}\)
Question 14.
The speed of the center of a wheel rolling on a horizontal surface is vQ. A point on the rim in level with the center will be moving at a speed of speed of,
(a) zero
(b) v0
(c) \(\sqrt{2}\)v0
(d) 2 v0
[PMT 1992, PMT 2003, IIT 2004]
Answer:
(c) \(\sqrt{2}\)v0
![]()
Question 15.
A round object of mass m and radius r rolls down without slipping along an inclined plane. The fractional force,
(a) dissipates kinetic energy as heat.
(b) decreases the rotational motion.
(c) decreases the rotational and transnational motion ,
(d) converts transnational energy into rotational energy [PMT 2005]
Answer:
(d) converts transnational energy into rotational energy
Samacheer Kalvi 11th Physics Motion of System of Particles and Rigid Bodies Short Answer Questions
Question 1.
Define center of mass.
Answer:
The center of mass of a body is defined as a point where the entire mass of the body appears to be concentrated.
Question 2.
Find out the center of mass for the given geometrical structures.
(a) Equilateral triangle
(b) Cylinder
(c) Square
Answer:
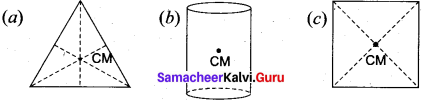
(a) For equilateral triangle, center of mass lies at its centro-id.
(b) For cylinder, center of mass lies at its geometrical center.
(c) For square, center of mass lies at the point where the diagonals meet.
Question 3.
Define torque and mention its unit.
Answer:
Torque is defined as the moment of the external applied force about a point or axis of rotation. The expression for torque is,
\(\vec{\tau}\) = \(\vec{r}\) x \(\vec{F}\)
Question 4.
What are the conditions in which force cannot produce torque?
Answer:
The forces intersect (or) passing through the axis of rotation cannot produce torque as the perpendicular distance between the forces is 0 i.e. r = 0.
∴ \(\vec{\tau}\) = \(\vec{r}\) x \(\vec{F}\) = 0
Question 5.
Give any two examples of torque in day – to – day life.
Answer:
- The opening and closing of a door about the hinges.
- Turning of a nut using a wrench.
Question 6.
What is the relation between torque and angular momentum?
Answer:
We have the expression for magnitude of angular momentum of a rigid body as, L = I ω. The expression for magnitude of torque on a rigid body is, τ = I α.
We can further write the expression for torque as,
τ = I\(\frac {dω}{dt}\) (∴ α = \(\frac {dω}{dt}\))
Where, ω is angular velocity and α is angular acceleration. We can also write equation,
τ = \(\frac {d(Iω)}{dt}\)
τ = \(\frac {dL}{dt}\)
![]()
Question 7.
What is equilibrium?
Answer:
A rigid body is said to be in mechanical equilibrium where both its linear momentum and angular momentum remain constant.
Question 8.
How do you distinguish between stable and unstable equilibrium?
Answer:
Stable Kquilibrium:
- The body tries to come back to equilibrium if slightly disturbed and released.
- The center of mass of the body shifts slightly higher if disturbed from equilibrium.
- Potential energy of the body is minimum and it increases if disturbed.
Unstable Equilibrium:
- The body cannot come back to equilibrium if slightly disturbed and released.
- The center of mass of the body shifts slightly lower if disturbed from equilibrium.
- Potential energy of the body is not minimum and it decreases if disturbed.
Question 9.
Define couple.
Answer:
A pair of forces which are equal in magnitude but opposite in direction and separated by a perpendicular distance so that their lines of action do not coincide that causes a turning effect is called a couple.
Question 10.
State principle of moments.
Answer:
Principle of moment states that when an object is in equilibrium the sum of the anticlockwise moments about a point is equal to the sum of the clockwise moments.
![]()
Question 11.
Define center of gravity.
Answer:
The center of gravity of a body is the point at which the entire weight of the body acts, irrespective of the position and orientation of the body.
Question 12.
Mention any two physical significance of moment of inertia
Answer:
Moment of inertia for point mass,
I = \(m_{i} r_{i}^{2}\)
Moment of inertia for bulk object,
I = ∑\(m_{i} r_{i}^{2}\)
Question 13.
What is radius of gyration?
Answer:
The radius of gyration of an object is the perpendicular distance from the axis of rotation to an equivalent point mass, which would have the same mass as well as the same moment of inertia of the object.
Question 14.
State conservation of angular momentum.
Answer:
The law of conservation of angular momentum states that when no external torque acts on the body the net angular momentum of a rotating rigid body remains constant.
Question 15.
What are the rotational equivalents for the physical quantities, (i) mass and (ii) force?
Answer:
The rotational equivalents for (i) mass and (ii) force are moment of inertia and torque respectively.
![]()
Question 16.
What is the condition for pure rolling?
Answer:
In pure rolling, there is no relative motion of the point of contact with the surface when the rolling object speeds up or shows down. It must accelerate or decelerate respectively.
Question 17.
What is the difference between sliding and slipping?
Sliding:
- Velocity of center of mass is greater than Rω i.e. VCM > Rω.
- Velocity of transnational motion is greater than velocity of rotational motion.
- Resultant velocity acts in the forward direction.
Slipping:
- Velocity of center of mass is lesser than Rω. i.e. VCM < Rω
- Velocity of translation motion is lesser than velocity of rotational motion.
- Resultant velocity acts in the backward direction.
Samacheer Kalvi 11th Physics Motion of System of Particles and Rigid Bodies Long Answer Questions
Question 1.
Explain the types of equilibrium with suitable examples.
Answer:
- Transnational motion – A book resting on a table.
- Rotational equilibrium – A body moves in a circular path with constant velocity.
- Static equilibrium – A wall – hanging, hanging on the wall.
- Dynamic equilibrium – A ball decends down in a fluid with its terminal velocity.
- Stable equilibrium – A table on the floor
- Unstable equilibrium – A pencil standing on its tip.
- Neutral equilibrium – A dice rolling on a game board.
Question 2.
Explain the method to find the center of gravity of a irregularly shaped lamina.
Answer:
There is also another way to determine the center of gravity of an irregular lamina. If we suspend the lamina from different points like P, Q, R as shown in figure, the vertical lines I PP’, QQ’, RR’ all pass through the center of gravity. Here, reaction force acting at the point of suspension and the gravitational force acting at the center of gravity cancel each other and the torques caused by them also cancel each other.
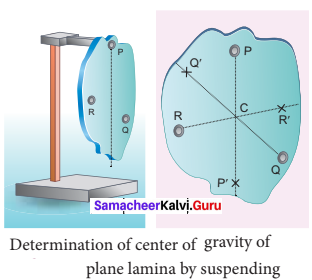
Determination of center of gravity of plane lamina by suspending
Question 3.
Explain why a cyclist bends while negotiating a curve road? Arrive at the expression for angle of bending for a given velocity.
Answer:
Let us consider a cyclist negotiating a circular level road (not banked) of radius r with a speed v. The cycle and the cyclist are considered as one system with mass m. The center gravity of the system is C and it goes in a circle of radius r with center at O. Let us choose the line OC as X – axis and the vertical line through O as Z – axis as shown in Figure.
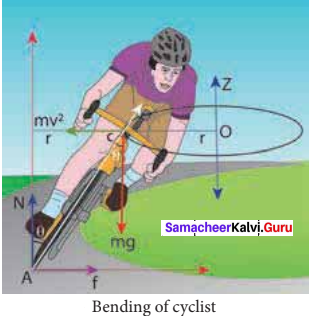
The system as a frame is rotating about Z – axis. The system is at rest in this rotating frame. To solve problems in rotating frame of reference, we have to apply a centrifugal force (pseudo force) on the system which will be \(\frac{m v^{2}}{r}\) This force will act through the center of gravity. The forces acting on the system are,
- gravitational force (mg)
- normal force (N)
- frictional force (f)
- centrifugal force (\(\frac{m v^{2}}{r}\)).
As the system is in equilibrium in the rotational frame of reference, the net external force and net external torque must be zero. Let us consider all torques about the point A in Figure.
For rotational equilibrium,
τnet = 0
The torque due to the gravitational force about point A is (mg AB) which causes a clockwise turn that is taken as negative. The torque due to the centripetal force is I BC which causes an (\(\frac{m v^{2}}{r}\) BC) Which causes an anticlockwise turn that is taken as positive.
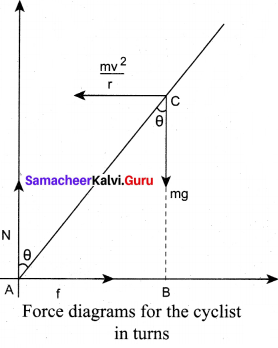

While negotiating a circular level road of radius r at velocity v, a cyclist has to bend by an angle 0 from vertical given by the above expression to stay in equilibrium (i.e. to avoid a fall).
![]()
Question 4.
Derive the expression for moment of inertia of a rod about its center and perpendicular to the rod.
Answer:
Let us consider a uniform rod of mass (M) and length (l) as shown in figure. Let us find an expression for moment of inertia of this rod about an axis that passes through the center of mass and perpendicular to the rod. First an origin is to be fixed for the coordinate system so that it coincides with the center of mass, which is also the geometric center of the rod. The rod is now along the x axis. We take an infinitesimally small mass (dm) at a distance (x) from the origin. The moment of inertia (dI) of this mass (dm) about the axis is, dI = (dm) x2
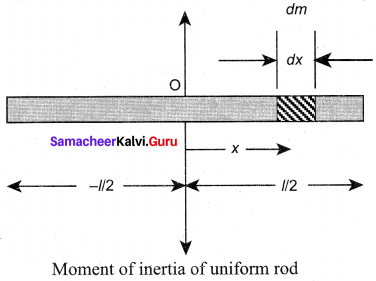
As the mass is uniformly distributed, the mass per unit length (λ) of the rod is, λ = \(\frac {M}{l}\)
The (dm) mass of the infinitesimally small length as, dm = λ dx = \(\frac {M}{l}\) dx
The moment of inertia (I) of the entire rod can be found by integrating dl,

As the mass is distributed on either side of the origin, the limits for integration are taken from to – l/2 to l/2.

Question 5.
Derive the expression for moment of inertia of a uniform ring about an axis passing through the center and perpendicular to the plane.
Answer:
Let us consider a uniform ring of mass M and radius R. To find the moment of inertia of the ring about an axis passing through its center and perpendicular to the plane, let us take an infinitesimally small mass (dm) of length (dx) of the ring. This (dm) is located at a distance R, which is the radius of the ring from the axis as shown in figure.
The moment of inertia (dl) of this small mass (dm) is,
dI = (dm)R2
The length of the ring is its circumference (2πR). As the mass is uniformly distributed, the mass per unit length (λ) is,
λ = \(\frac {mass}{lengh}\) = \(\frac {M}{2πR}\)
The mass (dm) of the infinitesimally small length is,
dm = λ dx = \(\frac {M}{2πR}\) dx
Now, the moment of inertia (I) of the entire ring is,
 To cover the entire length of the ring, the limits of integration are taken from 0 to 2πR.
To cover the entire length of the ring, the limits of integration are taken from 0 to 2πR.

Question 6.
Derive the expression for moment of inertia of a uniform disc about an axis passing through the center and perpendicular to the plane.
Answer:
Consider a disc of mass M and radius R. This disc is made up of many infinitesimally small rings as shown in figure. Consider one such ring of mass (dm) and thickness (dr) and radius (r). The moment of inertia (dl) of this small ring is,
dI = (dm)R2
As the mass is uniformly distributed, the mass per unit area (σ) is σ = \(\frac {mass}{area}\) = \(\frac{M}{\pi R^{2}}\)
The mass of the infinitesimally small ring is,
dm = σ 2πr dr = \(\frac{\mathrm{M}}{\pi \mathrm{R}^{2}}\) 2πr dr
where, the term (2πr dr) is the area of this elemental ring (2πr is the length and dr is the thickness), dm = \(\frac{2 \mathrm{M}}{\mathrm{R}^{2}}\) r dr
dI = \(\frac{2 \mathrm{M}}{\mathrm{R}^{2}}\) r3 dr
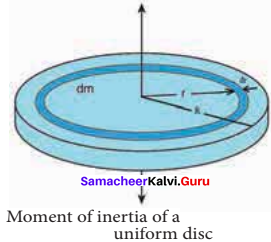 The moment of inertia (I) of the entire disc is,
The moment of inertia (I) of the entire disc is,

Question 7.
Discuss conservation of angular momentum with example.
Answer:
When no external torque acts on the body, the net angular momentum of a rotating rigid body remains constant. This is known as law of conservation of angular momentum.
τ = \(\frac {dL}{dt}\)
If τ = 0 then, L = constant.
As the angular momentum is L = Iω, the conservation of angular momentum could further be written for initial and final situations as,
Iiωi = Iiωi (or) Iω = constant
The above equations say that if I increases ω will decrease and vice – versa to keep the angular momentum constant.
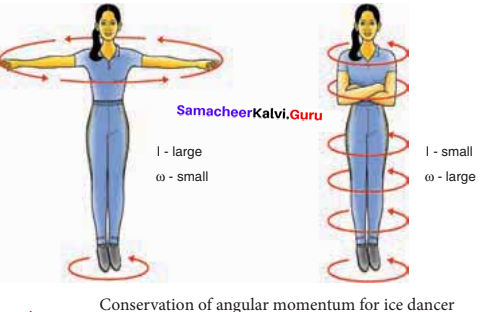
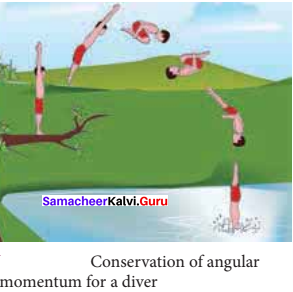
There are several situations where the principle of conservation of angular momentum is applicable. One striking example is an ice dancer as shown in Figure A. The dancer spins slowly when the hands are stretched out and spins faster when the hands are brought close to the body.
Stretching of hands away from body increases moment of inertia, thus the angular velocity decreases resulting in slower spin. When the hands are brought close to the body, the moment of inertia decreases, and thus the angular velocity increases resulting in faster spin. A diver while in air as in Figure B curls the body close to decrease the moment of inertia, which in turn helps to increase the number of somersaults in air.
Question 8.
State and prove parallel axis theorem.
Answer:
Parallel axis theorem:
Parallel axis theorem states that the moment of inertia of a body about any axis is equal to the sum of its moment of inertia about a parallel axis through its center of mass and the product of the mass of the body and the square of the perpendicular distance between the two axes.
If IC is the moment of inertia of the body of mass M about an axis passing through the center of mass, then the moment of inertia I about a parallel axis at a distance d from it is – given by the relation,
I = IC + M d2
Let us consider a rigid body as shown in figure. Its moment of inertia about an axis AB passing through the center of mass is IC. DE is another axis parallel to AB at a perpendicular distance d from AB. The moment of inertia of the body about DE is I. We attempt to get an expression for I in terms of IC. For this, let us consider a point mass m on the body at position x from its center of mass.
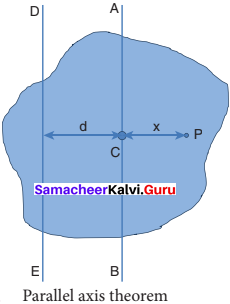
The moment of inertia of the point mass about the axis DE is, m (x + d)2. The moment of inertia I of the whole body about DE is the summation of the above expression.
I = ∑ m (x + d)2
This equation could further be written as,
I = ∑ m(x2 + d2 + 2xd)
1= ∑ (mx2 + md2 + 2 dmx)
l = ∑ mx2 + md2 + 2d ∑ mx
Here, ∑ mx2 is the moment of inertia of the body about the center of mass. Hence,IC = ∑ mx2
The term, ∑ mx = 0 because, x can take positive and negative values with respect to the axis AB. The summation (∑ mx) will be zero.
Thus, I = IC + ∑ m d2 = IC + (∑m) d2
Here, ∑ m is the entire mass M of the object (∑ m = M).
I = IC + Md2
![]()
Question 9.
State and prove perpendicular axis theorem.
Answer:
Perpendicular axis theorem:
This perpendicular axis theorem holds good only for plane laminar objects. The theorem states that the moment of inertia of a plane laminar body about an axis perpendicular to its plane is equal to the sum of moments of inertia about two perpendicular axes lying in the plane of the body such that all the three axes are mutually perpendicular and have a common point.
Let the X and Y – axes lie in the plane and Z – axis perpendicular to the plane of the laminar object. If the moments of inertia of the body about X and Y-axes are IX and IY respectively – and IZ is the moment of inertia about Z-axis, then the perpendicular axis theorem could be expressed as,
IZ = IX + IY
To prove this theorem, let us consider a plane laminar object of negligible thickness on which lies the origin (O). The X and Y – axes lie on the plane and Z – axis is perpendicular to it as shown in figure. The lamina is considered to be made up of a large number of particles of mass m. Let us choose one such particle at a point P which has coordinates (x, y) at a distance r from O.
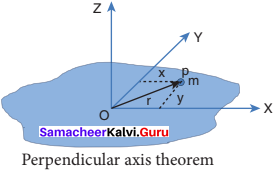
The moment of inertia of the particle about Z – axis is, mr2.
The summation of the above expression gives the moment of inertia of the entire lamina about Z – axis as, IZ = ∑ mr2
Here, r2 = x2 + y2
Then, IZ = ∑ m (x2 + y2)
IZ = ∑ m x2 + ∑ m y2
In the above expression, the term ∑ m x2 is the moment of inertia of the body about the Y-axis and similarly the term ∑ m y2is the moment of inertia about X- axis. Thus,
IX = ∑ m y2 and IY = ∑ m x2
Substituting in the equation for Iz gives,
IZ = IX + IY
Thus, the perpendicular axis theorem is proved.
Question 10.
Discuss rolling on inclined plane and arrive at the expression for the acceleration.
Answer:
Let us assume a round object of mass m and radius R is rolling down an inclined plane without slipping as shown in figure. There are two forces acting on the object along the inclined plane. One is the component of gravitational force (mg sin θ) and the other is the static frictional force (f). The other component of gravitation force (mg cos θ) is cancelled by the normal force (N) exerted by the plane. As the motion is happening along the incline, we shall write the equation for motion from the free body diagram (FBP) of the object.
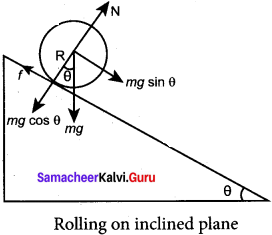
For transnational motion, mg sin θ is the supporting force and f is the opposing force, mg sin θ f = ma
For rotational motion, let us take the torque with respect to the center of the object. Then mg sin 0 cannot cause torque as it passes through it but the frictional force f can set torque of Rf = Iα
By using the relation, a = rα, and moment of inertia I = mK2 we get,
Rf = mK2 \(\frac {a}{R}\); f = ma \(\left(\frac{\mathrm{K}^{2}}{\mathrm{R}^{2}}\right)\)
Now equation becomes,
mg sin θ – ma \(\left(\frac{\mathrm{K}^{2}}{\mathrm{R}^{2}}\right)\) = ma
mg sin θ = ma + ma \(\left(\frac{\mathrm{K}^{2}}{\mathrm{R}^{2}}\right)\)
a \(\left(1+\frac{\mathrm{K}^{2}}{\mathrm{R}^{2}}\right)\) = g sin θ
After rewriting it for acceleration, we get,
a = \(\frac{g \sin \theta}{\left(1+\frac{K^{2}}{R^{2}}\right)}\)
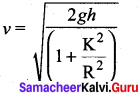
We can also find the expression for final velocity of the rolling object by using third equation of motion for the inclined plane.
v2 = u2 + 2as. If the body starts rolling from rest, u = 0. When h is the vertical height of the incline, the length of the incline s is, s = \(\frac {h}{sin θ}\)
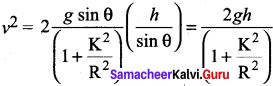 By taking square root,
By taking square root,
The time taken for rolling down the incline could also be written from first equation of motion as, v = u + at. For the object which starts rolling from rest, u = 0. Then,
t = \(\frac {v}{a}\)
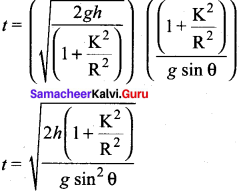
The equation suggests that for a given incline, the object with the least value of radius of gyration K will reach the bottom of the incline first.
Samacheer Kalvi 11th Physics Motion of System of Particles and Rigid Bodies Conceptual Questions
Question 1.
When a tree is cut, the cut is made on the side facing the direction in which the tree is required to fall. Why?
Answer:
A cut on the tree is made on the side facing the direction in which the tree is required to fall because that side will no longer be supported by the normal force from the bottom, therefore the gravitational force tries to rotate it. So the torque given by the gravity to the tree makes the tree fall on the side as anticipated.
![]()
Question 2.
Why does a porter bend forward while carrying a sack of rice on his back?
Answer:
When a porter carries a sack of rice, the line of action of his center of gravity will go away from the body. It affects the balance, to avoid this he bends. By which center of gravity will realign within the body again. So balance is maintained.
Question 3.
Why is it much easier to balance a meter scale on your finger tip than balancing on a match stick?
Answer:
A meter scale is larger then a match stick. So the center of gravity for meter scale is higher than a matchstick when we keep it vertically. It is easier to balance the object whose center of gravity is higher than the object whose centro of gravity is lower. So, it is hard to balance a match stick than a meter scale.
Question 4.
Two identical water bottles one empty and the other filled with water are allowed to roll down an inclined plane. Which one of them reaches the bottom first? Explain your answer.
Answer:
Mass of the empty water bottle mostly concentrated on its surface. So moment of inertia of empty water bottle is more than the bottle filled with water. As we know, moment of inertia is inversely proportional to angular velocity. Therefore, the bottle filled with water whirls with greater speed and reaches the ground first.
Question 5.
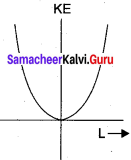
Write the relation between angular momentum and rotational kinetic energy. Draw a graph for the same. For two objects of same angular momentum, compare the moment of inertia using the graph.
Answer:
Let a rigid body of moment of inertia I rotate with angular velocity ω.
The angular momentum of a rigid body is, L = Iω
The rotational kinetic energy of the rigid body is, KE = \(\frac { 1 }{ 2 }\) Iω2.
By multiplying the numerator and denominator of the above equation with I, we get a relation between L and KE as,

It resembles with y = Kx2. If angular momentum is same for two objects, kinetic energy is inversely proportional to moment of inertia.
Moment of inertia of the object whose kinetic energy is lesser will have greater magnitude.
Question 6.
Three identical solid spheres move down through three inclined planes A, B and C all same dimensions. A is without friction, B is undergoing pure rolling and C is rolling with slipping. Compare the kinetic energies EA, EB and EC at the bottom.
Answer:
Even though, the three identical solid spheres of same dimensions move down through three different inclined plane, according to the law of conservation of energy, the potential energy possessed by these three solid spheres will be converted into kinetic energies. So the kinetic energies EA, EB and EC are equal at the bottom.
![]()
Question 7.
Give an example to show that the following statement is false. Any two forces acting on a body can be combined into single force that would have same effect.
Answer:
A single force i.e. resultant of two forces acting on a body depends upon the angle between them also. The simple example for this is if two forces 5 N and 5 N acting on the object in the opposite direction, the single resultant force acting on the body is zero. But, if two forces acting on the object along the same direction, then the resultant i.e. the single force is 5 + 5 = 10 N. Hence the given statement “any two forces acting on a body can be combined into single force that would leave same effect” is wrong.
Samacheer Kalvi 11th Physics Motion of System of Particles and Rigid Bodies Numerical Problems
Question 1.
A uniform disc of mass 100 g has a diameter of 10 cm. Calculate the total energy of the disc when rolling along a horizontal table with a velocity of 20 cm s-2.
Answer:
Given,
Mass of the disc = 100 g = 100 x 10-3 kg = \(\frac { 1 }{ 10 }\)kg
Velocity of disc = 20 cm s-1 = 20 x 10-2 ms-1 = 0.2 ms-1
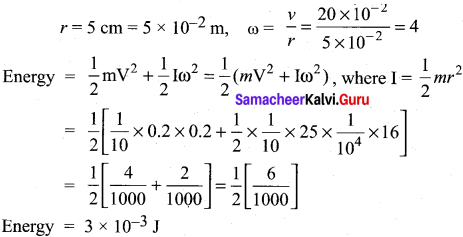
Question 2.
A particle of mass 5 units is moving with a uniform speed of v = \(3 \sqrt{2}\) units in the XOY plane along the line y = x + 4. Find the magnitude of angular momentum.
Answer:
Given,
Mass = 5 units
Speed = v = \(3 \sqrt{2}\) units
Y = X + 4
Angular momentum = L = m(\(\bar{r} \times \bar{v}\))
= m(x\(\hat{i}\) +y\(\hat{j}\))x(v\(\hat{i}\) + v\(\hat{j}\)) = m[xv\(\hat{k}\)-vy\(\hat{k}\)] = m[xv\(\hat{k}\)– v(x + 4)\(\hat{k}\)]
L = -mv\(\hat{k}\) = -4 x 5 x \(3 \sqrt{2}\)\(\hat{k}\) = – 60\(\sqrt{2}\)\(\hat{k}\)
L = 60\(\sqrt{2}\) units.
Question 3.
A fly wheel rotates with a uniform angular acceleration. If its angular velocity increases from 20π rad/s to 40π rad/s in 10 seconds, find the number of rotations in that period.
Answer:
Given,
Initial angular velocity ω0 = 20 π rad/s
Final angular velocity ω = 40 π rad/s
Time t = 10 s
Solution:
Angular acceleration α = \(\frac{\omega-\omega_{0}}{t}\) = \(\frac {40π – 20π }{ 10 }\)
α = 2π rad/s2
According to equation of motion for rotational motion
![]()
The number of rotations = n = \(\frac {θ}{ 2π }\)
n = \(\frac {300π}{ 2π }\) = 150 rotations.
![]()
Question 4.
A uniform rod of mass m and length / makes a constant angle 0 with an axis of rotation which passes through one end of the rod. Find the moment of inertia about this gravity is.
Answer:
Moment of inertia of the rod about the axis which is passing through its center of gravity is
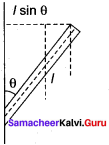
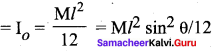
Moment of inertia of a uniform rod of mass m and length l about one axis which passes through one end of the rod
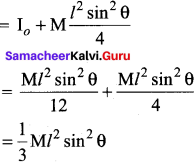
Question 5.
Two particles P and Q of mass 1 kg and 3 kg respectively start moving towards each other from rest under mutual attraction. What is the velocity of their center of mass?
Answer:
Given,
Mass of particle P = 1 kg Mass of particle Q = 3 kg
Solution:
Particles P and Q forms a system. Here no external force is acting on the system,
We know that M = \(\frac {d}{dt}\) (VCM ) = f
It means that, C.M. of an isolated system remains at rest when no external force is acting and internal forces do not change its center of mass.
Question 6.
Find the moment of inertia of a hydrogen molecule about an axis passing through its center of mass and perpendicular to the inter-atomic axis.
Given: mass of hydrogen atom 1.7 x 1027kg and inter atomic distance is equal to 4 x 10-10m.
Answer:
Given,
Inter-atomic distance : 4 x 10-10 m
Mass of H2 atom : 1.7 x 10-27 kg
Moment of inertia of H2 =


Question 7.
On the edge of a wall, we build a brick tower that only holds because of the bricks’ own weight. Our goal is to build a stable tower whose overhang d is greater than the length l of a single brick. What is the minimum number of bricks you need?
(Hint: Find the center of mass for each brick and add.)
Answer:
Given:
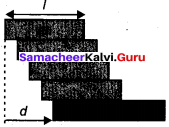
Length of the brick = l
Length of the overhang = d
The mono of bricks can be decided only by using the concept of position of center of gravity. The first brick is in contact with the ground and it will not fall over.
Let one end of brick 2 is coinciding with the center of brick 1 i.e. x = 0.
∴ The position of n brick is
xn = (n – 1) \(\frac {L}{4}\)
The center of gravity is in the midway between the center of brick 2 and the center of brick n.
position of G =

brick tower will fall when G >\(\frac {L}{4}\) it shows that n > 4.
Question 8.
The 747 boing plane is landing at a speed of 70 m s-1. Before touching the ground, the wheels are not rotating. How long a skid mark do the wing wheels leave (assume their mass is 100 kg which is distributed uniformly, radius is 0.7 m, and the coefficient of friction with the ground is 0.5)?
Answer:
The types of the plane will leave a skid mark if the speed of the types in contact with ground is lesser than the velocity of the plane. The condition for this is –
v > ω
(When the type attained an angular velocity of V/R)
The types will stop the skidding and starts the rolling.
The forces acting on the wheel after the plane touches down are,
N – P Normal force W – weight
The wheel is not accelerating means
N = ω
The torque about the center of the wheel is
τ = RF = µωR
The angular acceleration is

According to equation of motion, time taken to stop the skidding by the wheel is,

The six mark will have a length of
l = vt = 70 x 0.03 = 2.1 m
Note:
The 747 is resting on the runway, supported by 16 wheels under the wing, and 2 under the nose total length is 68.63 m. The normal force experienced by plane through its 16 wheels is ω = 232 KN.
Samacheer Kalvi 11th Physics Motion of System of Particles and Rigid Bodies Additional Questions Solved
Samacheer Kalvi 11th Physics Motion of System of Particles and Rigid Bodies Multiple Choice Questions
Question 1.
The changes produced by the deforming forces in a rigid body are –
(a) very large
(b) infinity
(c) negligibly small
(d) small
Answer:
(c) negligibly small
Question 2.
When a rigid body moves all particles that constitute the body follows-
(a) same path
(b) different paths
(c) either same or different path
(d) circular path
Answer:
(b) different path
Question 3.
For bodies of regular shape and uniform mass distribution, the center of mass is at –
(a) the comers
(b) inside the objects
(c) the point where the diagonals meet
(d) the geometric center
Answer:
(d) the geometric center
![]()
Question 4.
For square and rectangular objects center of mass lies at –
(a) the point where the diagonals meet
(b) at the comers
(c) on the center surface
(d) any point
Answer:
(a) the point where the diagonals meet
Question 5.
Center of mass may lie –
(a) within the body
(b) outside the body
(c) both (a) and (b)
(d) only at the center
Answer:
(c) both (a) and (b)
Question 6.
The dimension of point mass is –
(a) positive
(b) negative
(c) zero
(d) infinity
Answer:
(c) zero
Question 7.
The motion of center of mass of a system of two particles is unaffected by their internal forces –
(a) irrespective of the actual directions of the internal forces
(b) only if they are along the line joining the particles
(c) only if acts perpendicular to each other
(d) only if acting opposite
Answer:
(a) irrespective of the actual directions of the internal forces
Question 8.
A circular plate of diameter 10 cm is kept in contact with a square plate of side 10 cm. The density of the material and the thickness are same everywhere. The center of mass of the system will be
(a) inside the circular plate
(b) inside the square plate
(c) At the point of contact
(d) outside the system
Answer:
(6) inside the square plate
Question 9.
The center of mass of a system of particles does not depend on
(a) masses of particles
(b) position of the particles
(c) distribution of masses
(d) forces acting on the particles
Answer:
(d) forces acting on the particles
![]()
Question 10.
The center of mass of a solid cone along the line from the center of the base to the vertex is at –
(a) \(\frac { 1 }{ 2 }\) th of its height
(b) \(\frac { 1 }{ 3 }\) of its height
(c) \(\frac { 1 }{ 4 }\) th of its height
(d) \(\frac { 1 }{ 5 }\) th of its height
Answer:
(d) \(\frac { 1 }{ 5 }\) th of its height
Question 11.
All the particles of a body are situated at a distance of X from origin. The distance of the center of mass from the origin is –
(a) ≥ r
(b) ≤ r
(c) = r
(d) > r
Question
A free falling body breaks into three parts of unequal masses. The center of mass of the three parts taken together shifts horizontally towards –
(a) heavier piece
(b) lighter piece
(c) does not shift horizontally
(d) depends on vertical velocity
Answer:
(c) does not shift horizontally
Question 13.
The distance between the center of carbon and oxygen atoms in the gas molecule is 1.13 A. The center of mass of the molecule relative to oxygen atom is –
(a) 0.602 Å
(b) 0.527 Å
(c) 1.13 Å
(d) 0.565 Å
Answer:
(b) 0.527 Å
Given,
Inter atomic distance = 1.13 Å
Mass of carbon atom = 14
Mass of oxygen atom = 16
Let C.M. of molecule lies at a distance of X from oxygen atom-
i.e. m1r1 = m2r2
16 X = 14(1.13 – X)
30 X = 15.82
X = 0.527 Å
Question 14.
The unit of position vector of center of mass is-
(a) kg
(b) kg m2
(c) m
(d) m2
Answer:
(c) m
Question 15.
The sum of moments of masses of all the particles in a system about the center of mass is-
(a) minimum
(b) maximum
(c) zero
(d) infinity
Answer:
(c) zero
Question 16.
The motion of center of mass depends on-
(a) external forces acting on it
(b) internal forces acting within it
(c) both (a) and (b)
(d) neither (a) nor (b)
Answer:
(a) external forces acting on it
![]()
Question 17.
Two particles P and Q move towards with each other from rest with the velocities of 10 ms-1 and 20 ms-1 under the mutual force of attraction. The velocity of center of mass is-
(a) 15 ms-1
(b) 20 ms-1
(c) 30 ms-1
(d) zero
Answer:
(d) zero
Question 18.
The reduced mass of the system of two particles of masses 2 m and 4 m will be –
(a) 2 m
(b) \(\frac {2 }{ 3 }\)y m
(c) \(\frac {3}{ 2 }\)y m
(d) \(\frac { 4 }{ 3 }\)m
Answer:
(d) \(\frac { 4 }{ 3 }\)m
Question 19.
The motion of the center of mass of a system consists of many particles describes its –
(a) rotational motion
(b) vibratory motion
(c) oscillatory motion
(d) translator y motion
Answer:
(c) oscillatory motion
Question 20.
The position of center of mass can be written in the vector form as –

Answer:
![]()
Question 21.
The positions of two masses m1 and m2 are x1 and x2. The position of center of mass is –

Answer:
![]()
Question 22.
In a two particle system, one particle lies at origin another one lies at a distance of X. Then the position of center of mass of these particles of equal mass is –

Answer:
(a) \(\frac {X}{2}\)
Question 23.
Principle of moments is –

Answer:
![]()
Question 24.
Infinitesimal quantity means –
(a) collective particles
(b) extremely small
(c) nothing
(d) extremely larger
Answer:
(b) extremely small
![]()
Question 25.
In the absence of external forces the center of mass will be in a state of –
(a) rest
(b) uniform motion
(c) may be at rest or in uniform motion
(d) vibration
Answer:
(c) may be at rest or in uniform motion
Question 26.
The activity of the force to produce rotational motion in a body is called as –
(a) angular momentum
(b) torque
(c) spinning
(d) drive force
Answer:
(b) torque
Question 27.
The moment of the external applied force about a point or axis of rotation is known as –
(a) angular momentum
(b) torque
(c) spinning
(d) drive force
Answer:
(b) torque
Question 28.
Torque is given as –
(a) \(\vec{r}\) . \(\vec{F}\)
(b) \(\vec{r}\) x \(\vec{F}\)
(c) \(\vec{F}\) x \(\vec{r}\)
(d) r F cos θ
Answer:
(b) \(\vec{r}\) x \(\vec{F}\)
Question 29.
The magnitude of torque is –
(a) rF sin θ
(b) rF cos θ
(c) rF tan θ
(d) rF
Answer:
(a) rF sin θ
Question 30.
The direction of torque ácts –
(a) along \(\vec{F}\)
(b) along \(\vec{r}\) & \(\vec{F}\)
(c) Perpendicular to \(\vec{r}\)
(d) Perpendicular to both \(\vec{r}\) & \(\vec{F}\)
Answer:
(d) Perpendicular to both \(\vec{r}\) & \(\vec{F}\)
![]()
Question 31.
The unit of torque is –
(a) is
(b) Nm-2
(c) Nm
(d) Js-1
Answer:
(c) Nm
Question 32.
The direction of torque is found using –
(a) left hand rule
(b) right hand rule
(c) palm rule
(d) screw rule
Answer:
(b) right hand rule
Question 33.
if the direction of torque is out of the paper then the rotation produced by the torque is –
(a) clockwise
(b) anticlockwise
(c) straight line
(d) random direction
Answer:
(a) clockwise
Question 34.
If the direction of the torque is inward the paper then the rotation is –
(a) clockwise
(b) anticlockwise
(c) straight line
(d) random direction
Answer:
(a) clockwise
Question 35.
if \(\vec{r}\) and \(\vec{F}\) are parallel or anti parallel, then the torque is –
(a) zero
(b) minimum
(c) maximum
(d) infinity
Answer:
(a) zero
Question 36.
The maximum possible value of torque is –
(a) zero
(b) infinity
(c) \(\vec{r}\) + \(\vec{F}\)
(d) rF
Answer:
(d) rF
![]()
Question 37.
The relation between torque and angular acceleration is –
(a) \(\vec{τ}\) = \(\frac{1}{\alpha}\)
(b) \(\vec{α}\) = \(\frac{\vec{\tau}}{\mathrm{I}}\)
(c) \(\vec{α}\) = I \(\vec{τ}\)
(d) \(\vec{τ}\) = \(\frac{\vec{\alpha}}{\mathrm{I}}\)
Answer:
(b) \(\vec{α}\) = \(\frac{\vec{\tau}}{\mathrm{I}}\)
Question 38.
Angular momentum is –
(a) \(\vec{P}\) x \(\vec{r}\)
(b) \(\vec{r}\) x \(\vec{P}\)
(c) \(\overrightarrow{\frac{r}{\vec{p}}}\)
(d) \(\vec{r}\) . \(\vec{P}\)
Answer:
(b) \(\vec{r}\) x \(\vec{P}\)
Question 39.
The magnitude of angular momentum is given by –
(a) rp
(b) rp sin θ
(c) rp cos θ
(d) rp tan θ
Answer:
(b) rp sin θ
Question 40.
Angular momentum is associated with –
(a) rotational motion
(b) linear motion
(c) both (a) and (b)
(d) circular motion only
Answer:
(c) both (a) and (b)
Question 41.
Angular momentum acts perpendicular to –
(a) \(\vec{r}\)
(b) \(\vec{P}\)
(c) both \(\vec{r}\) and \(\vec{P}\)
(d) plane of the paper
Answer:
(c) both \(\vec{r}\) and \(\vec{P}\)
Question 42.
Angular momentum is given by –
(a) \(\frac {I}{ω}\)
(b) τω
(c) Iω
(d) \(\frac {ωI}{2}\)
Answer:
(c) Iω
![]()
Question 43.
The rate of change of angular momentum is –
(a) Torque
(b) angular velocity
(c) centripetal force
(d) centrifugal force
Answer:
(a) Torque
Question 44.
The forces acting on a body when it is at rest –
(a) is gravitational force
(b) Normal force
(c) both gravitational as well as normal force
(d) No force is acting
Answer:
(c) both gravitational as well as normal force
Question 45.
The net force acting on a body when it is at rest is –
(a) gravitational force
(b) Normal force
(c) Sum of gravitational and normal force
(d) zero
Answer:
(d) zero
Question 46.
If net force acting on a body is zero, then the body is in –
(a) transnational equilibrium
(b) rotational equilibrium
(c) both (a) and (b)
(d) none
Answer:
(a) transnational equilibrium
Question 47.
If the net torque acting on the body is zero, then the body is in –
(a) transnational equilibrium
(b) rotational equilibrium
(c) mechanical equilibrium
(d) none
Answer:
(b) rotational equilibrium
![]()
Question 48.
when the net force and net torque acts on the body is zero then the body is in –
(a) transnational equilibrium
(b) rotational equilibrium
(c) mechanical equilibrium
(d) none
Answer:
(d) none
Question 49.
When the net force and net torque acts on the body is zero then the body is in –
(a) static equilibrium
(b) Dynamic equilibrium
(c) both (a) and (b)
(d) transnational equilibrium
Answer:
(c) both (a) and (b)
Question 50.
When two equal and opposite forces acting on the body at two different points, it may give –
(a) net force
(b) torque
(c) stable equilibrium
(d) none
Answer:
(b) torque
Question 51.
The torque in rotational motion is analogous to in transnational motion –
(a) linear momentum
(b) mass
(c) couple
(d) force
Answer:
(d) force
Question 52.
Which of the following example does not constitute a couple?
(a) steering a car
(b) turning a pen cap
(c) ball rolls on the floor
(d) closing the door
Answer:
(c) ball rolls on the floor
Questioner 53.
If the linear momentum and angular momentum are zero, then the object is said to be in –
(a) stable equilibrium
(b) unstable equilibrium
(c) neutral equilibrium
(d) all the above
Answer:
(d) all the above
Question 54.
When the body is disturbed, the potential energy remains same, then the body is in –
(a) stable equilibrium
(b) unstable equilibrium
(c) neutral equilibrium
(d) all the above
Answer:
(c) neutral equilibrium
![]()
Question 55
The point where the entire weight of the body acts is called as –
(a) center of mass
(b) center of gravity
(c) both (a) and (b)
(d) pivot
Answer:
(b) center of gravity
Question 56.
The forces acting on a cyclist negotiating a circular Level road is /are –
(a) gravitational force
(b) centrifugal force
(c) frictional force
(d) all the above
Answer:
(d) all the above
Question 57.
While negotiating a circular level road a cyclist has to bend by an angle θ from vertical to stay in an equilibrium is-
(a) \(\tan \theta=\frac{r g}{r^{2}}\)
(b) θ = \(\tan ^{-1}\left(\frac{v^{2}}{r g}\right)\)
(c) θ = \(\sin ^{-1}\left(\frac{r g}{r^{2}}\right)\)
(d) zero
Answer:
(b) θ = \(\tan ^{-1}\left(\frac{v^{2}}{r g}\right)\)
Question 58.
Moment of inertia for point masses –
(a) m2r
(b) rw2
(c) mr2
(d) zero
Answer:
(c) mr2
Question 59.
Moment of inertia for bulk object –
(a) rm2
(b) rw2
(c) \(m_{i} r_{i}^{2}\)
(d) \(\Sigma m_{i} r_{i}^{2}\)
Answer:
(d) \(\Sigma m_{i} r_{i}^{2}\)
Question 60.
For rotational motion, moment of inertia is a measure of –
(a) transnational inertia
(b) mass
(c) rotational inertia
(d) invariable quantity
Answer:
(c) rotational inertia
![]()
Question 61.
Unit of moment of inertia –
(a) kgm
(b) mkg-2
(c) kgm2
(d) kgm-1
Answer:
(c) kgm2
Question 62.
Dimensional formula for moment of inertia is –
(a) [ML-2]
(b) [M2L-1]
(c) [M-2]
(d) [ML2]
Answer:
(d) [ML2]
Question 63.
Moment of inertia of a body is a –
(a) variable quantity
(b) invariable quantity
(c) constant quantity
(d) measure of torque
Answer:
(a) variable quantity
Question 64.
Moment of inertia of a thin uniform rod about an axis passing through the center of mass and perpendicular to the length is –
(a) \(\frac { 1 }{ 3 }\)Ml2
(b) \(\frac { 1 }{ 12 }\)Ml2
(c) \(\frac { 1 }{ 2 }\)M(l2 + b2 )
(d) Ml2
Answer:
(b) \(\frac { 1 }{ 12 }\)Ml2
Question 65.
Moment of inertia ofa thin uniform rod about an axis passing through one end and perpendicular to the length is-
(a) \(\frac { 1 }{ 3 }\)Ml2
(b) \(\frac { 1 }{ 12 }\)Ml2
(c) \(\frac { 1 }{ 2 }\)M(l2 + b2 )
(d) Ml2
Answer:
(a) \(\frac { 1 }{ 3 }\)Ml2
Question 66.
Moment of inertia of a thin uniform rectangular sheet about an axis passing through the center of mass and perpendicular to the plane of the sheet is-
(a) \(\frac { 1 }{ 3 }\)Ml2
(b) \(\frac { 1 }{ 12 }\)Ml2
(c) \(\frac { 1 }{ 2 }\)M(l2 + b2 )
(d) Ml2
Answer:
(c) \(\frac { 1 }{ 2 }\)M(l2 + b2 )
![]()
Question 67.
Moment of inertia of a thin uniform ring about an axis passing through the center of gravity and perpendicular to the plane is –
(a) MR2
(b) 2 MR2
(c) \(\frac { 1 }{ 2 }\)MR2
(d) \(\frac { 3 }{ 2 }\)MR2
Answer:
(a) MR2
Question 68.
Moment of inertia of a thin uniform ring about an axis passing through the center and lying on the plane (along diameter) is –
(a) MR2
(b) 2 MR2
(c) \(\frac { 1 }{ 2 }\) MR2
(d) \(\frac { 2 }{ 3 }\)MR2
Answer:
(c) \(\frac { 1 }{ 2 }\) MR2
Question 69.
Moment of inertia of a thin uniform disc about an axis passing through the center and perpendicular to the plane is –
(a) MR2
(b) 2 MR2
(c) \(\frac { 1 }{ 2 }\) MR2
(d) \(\frac { 2 }{ 3 }\)MR2
Answer:
(c) \(\frac { 1 }{ 2 }\) MR2
Question 70.
Moment of inertia of a thin uniform disc about an axis passing through the center lying on the plane (along diameter is)
(a) MR2
(b) \(\frac { 1 }{ 2 }\) MR2
(c) \(\frac { 3 }{ 2 }\) MR2
(d) \(\frac { 1 }{ 4 }\) MR2
Answer:
(d) \(\frac { 1 }{ 4 }\) MR2
Question 71.
Moment of inertia of a thin uniform hollow cylinder about an axis of the cylinder is –
(a) MR2
(b) \(\frac { 1 }{ 2 }\) MR2
(c) \(\frac { 3 }{ 2 }\) MR2
(d) \(\frac { 1 }{ 4 }\) MR2
Answer:
(a) MR2
Question 72.
Moment of inertia of a thin uniform hollow cylinder about an axis of the cylinder is –
(a) MR2
(b) M\(\left(\frac{\mathrm{R}^{2}}{2}+\frac{l^{2}}{12}\right)\)
(c) \(\frac { 1 }{ 2 }\) MR2
(d) M\(\left(\frac{\mathrm{R}^{2}}{4}+\frac{l^{2}}{12}\right)\)
Answer:
(b) M\(\left(\frac{\mathrm{R}^{2}}{2}+\frac{l^{2}}{12}\right)\)
Question 73.
Moment of inertia of a uniform solid cylinder about an axis passing through the center and along the axis of the cylinder is –
(a) MR2
(b) M\(\left(\frac{\mathrm{R}^{2}}{2}+\frac{l^{2}}{12}\right)\)
(c) \(\frac { 1 }{ 2 }\) MR2
(d) M\(\left(\frac{\mathrm{R}^{2}}{4}+\frac{l^{2}}{12}\right)\)
Answer:
(c) \(\frac { 1 }{ 2 }\) MR2
![]()
Question 74.
Moment of inertia of a uniform solid cylinder about as axis passing perpendicular to the length and passing through the center is –
(a) MR2
(b) M\(\left(\frac{\mathrm{R}^{2}}{2}+\frac{l^{2}}{12}\right)\)
(c) \(\frac { 1 }{ 2 }\) MR2
(d) M\(\left(\frac{\mathrm{R}^{2}}{4}+\frac{l^{2}}{12}\right)\)
Answer:
(d) M\(\left(\frac{\mathrm{R}^{2}}{4}+\frac{l^{2}}{12}\right)\)
Question 75.
Moment of inertia of a thin hollow sphere about an axis passing through the center along its diameter is
(a) \(\frac { 2 }{ 3 }\)MR2
(b) \(\frac { 5 }{ 3 }\)MR2
(c) \(\frac { 7 }{ 5 }\)MR2
(d) \(\frac { 2 }{ 5 }\)MR2
Answer:
(a) \(\frac { 2 }{ 3 }\)MR2
Question 76.
Moment of inertia of a thin hollow sphere about an axis passing through the edge along its tangent is –
(a) \(\frac { 2 }{ 3 }\)MR2
(b) \(\frac { 5 }{ 3 }\)MR2
(c) \(\frac { 7 }{ 5 }\)MR2
(d) \(\frac { 2 }{ 5 }\)MR2
Answer:
(b) \(\frac { 5 }{ 3 }\)MR2
Question 77.
torment of inertia of a uniform solid sphere about an axis passing through the center along its diameter is –
(a) \(\frac { 2 }{ 3 }\)MR2
(b) \(\frac { 5 }{ 3 }\)MR2
(c) \(\frac { 7 }{ 5 }\)MR2
(d) \(\frac { 2 }{ 5 }\)MR2
Answer:
(d) \(\frac { 2 }{ 5 }\)MR2
Question 78.
Moment of inertia of a uniform solid sphere about an axis passing through the edge along its tangent is –
(a) \(\frac { 2 }{ 3 }\)MR2
(b) \(\frac { 5 }{ 3 }\)MR2
(c) \(\frac { 7 }{ 5 }\)MR2
(d) \(\frac { 2 }{ 5 }\)MR2
Answer:
(c) \(\frac { 7 }{ 5 }\)MR2
Question 79.
The ratio of K2/R2 of a thin uniform ring about an axis passing through the center and perpendicular to the plane is-
(a) 1
(b) 2
(c) \(\frac { 7 }{ 5 }\)
(d) \(\frac { 3 }{ 2 }\)
Answer:
(a) 1
![]()
Question 80.
The ratio of K2/ R2 of a thin uniform disc about an axis passing through the center and perpendicular to the plane is –
(a) 1
(b) 2
(c) \(\frac {1}{ 2 }\)
(d) \(\frac { 3 }{ 2 }\)
Answer:
(c) \(\frac {1}{ 2 }\)
Question 81.
When no external torque acts on the body, the net angular momentum of a rotating body.
(a) increases
(b) decreases
(c) increases or decreases
(d) remains constant
Answer:
(d) remains constant
Question 82.
Moment of inertia of a body is proportional to –
(a) ω
(b) \(\frac { 1 }{ ω }\)
(c) ω2
(d) \(\frac{1}{\omega^{2}}\)
Answer:
(b) \(\frac { 1 }{ ω }\)
Question 83.
When the hands are brought closer to the body, the angular velocity of the ice dancer –
(a) decreases
(b) increases
(c) constant
(d) may decrease or increase
Answer:
(b) increases
Question 84.
When the hands are stretched out from the body, the moment of inertia of the ice dancer –
(a) decreases
(b) increases
(c) constant
(d) may decrease or increase
Answer:
(b) increases
Question 85.
The work done by the torque is –
(a) F. ds
(b) F. dθ
(c) τ dθ
(d) r.dθ
Answer:
(c) τ dθ
Question 86.
Rotational Kinetic energy of a body is –
(a) \(\frac { 1 }{ 2 }\)mr
(b) \(\frac { 1 }{ 2 }\) Iω2
(c) \(\frac { 1 }{ 2 }\)Iv2
(d) \(\frac { 1 }{ 2 }\)mω2
Answer:
(b) \(\frac { 1 }{ 2 }\) Iω2
![]()
Question 87.
Rotational kinetic energy is given by –
(a) \(\frac { 1 }{ 2 }\)mr
(b) \(\frac { 1 }{ 2 }\)Iv2
(c) \(\frac{\mathrm{L}^{2}}{2 \mathrm{I}}\)
(d) \(\frac{2 \mathrm{I}}{\mathrm{L}^{2}}\)
Answer:
(c) \(\frac{\mathrm{L}^{2}}{2 \mathrm{I}}\)
Question 88.
If E is a rotational kinetic energy then angular momentum is-
(a) \(\sqrt{2 \mathrm{IE}}\)
(b) \(\frac{\mathrm{E}^{2}}{2 \mathrm{I}}\)
(c) \(\frac{2 \mathrm{I}}{\mathrm{E}^{2}}\)
(d) \(\frac{E}{I^{2} \omega^{2}}\)
Answer:
(a) \(\sqrt{2 \mathrm{IE}}\)
Question 89.
The product of torque acting on a body and angular velocity is –
(a) Energy
(b) power
(c) work done
(d) kinetic energy
Answer:
(b) power
Question 90.
The work done per unit time in rotational motion is given by –
(a) \(\vec{F}\) .v
(b) \(\frac {dθ}{dt}\)
(c) τ ω
(d) I ω
Answer:
(c) τ ω
Question 91.
While rolling, the path of center of mass of an object is –
(a) straight line
(b) parabola
(c) hyperbola
(d) circle
Answer:
(a) straight line
Question 92.
In pure rolling, the velocity of the point of the rolling object which comes in contact with the surface is –
(a) maximum
(b) minimum
(c) zero
(d) 2 VCM
Answer:
(c) zero
Question 93.
In pure rolling velocity of center of mass is equal to –
(a) zero
(b) Rω
(c) \(\frac { ω }{ R }\)
(d) \(\frac { R }{ ω }\)
Answer:
(b) Rω
![]()
Question 94.
In pure rolling, rotational velocity of points at its edges is equal to-
(a) Rω
(b) velocity of center of mass
(c) transnational velocity
(d) all the above
Answer:
(a) Rω
Question 95.
Sliding of the object occurs when –
(a) Vtrans < Vrot
(b) Vtrans = Vrot
(c) Vtrans > Vrot
(d) Vtrans = 0
Answer:
(c) Vtrans > Vrot
Question 96.
Sliding of the object occurs while –
(a) Vtrans = Vrot
(b) VCM = Rω
(c) VCM < Rω
(d) VCM > Rω
Answer:
(d) VCM > Rω
Question 97.
Slipping of the object occurs when –
(a) Vtrans < Vrot
(b) Vtrans = Vrot
(c) Vtrans > Vrot
(d) Vtrans = 0
Answer:
(a) Vtrans < Vrot
Question 98.
Slipping of the object occurs when –
(a) Vtrans = Vrot
(b) VCM = Rω
(c) VCM < Rω
(d) VCM > Rω
Answer:
(c) VCM < Rω
Question 99.
In sliding, the resultant velocity of a point of contact acts along –
(a) forward direction
(b) backward direction
(c) either (a) or (b)
(d) tangential direction
Answer:
(a) forward direction
Question 100.
In slipping, the resultant velocity of a point of contact acts along –
(a) forward direction
(b) backward direction
(c) either (a) or (b)
(d) tangential direction
Answer:
(b) backward direction
![]()
Question 101.
When a solid sphere is undergoing pure rolling, the ratio of transnational kinetic energy to rotational kinetic – energy is –
(a) 2 : 5
(b) 5 : 2
(c) 1 : 5
(d) 5 : 1
Answer:
(b) 5 : 2
Question 102.
Time taken by the rolling object in inclined plane to reach its bottom is –
Answer:
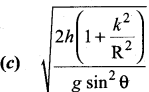
Question 103.
The velocity of the rolling object on inclined plane at the bottom of inclined plane is –
Answer:
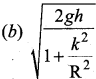
Question 104.
Moment of inertia of an annular disc about an axis passing through the centre and perpendicular to the plane of disc is –

Answer:
![]()
Question 105.
Moment of inertia of a cube about an axis passing through the center of mass and perpendicular to face is –
(a) \(\frac{\mathrm{Ma}^{2}}{6}\)
(b) \(\frac {1}{3}\) Ma2
(c) \(\frac {Ma}{6}\)
(d) \(\frac{\mathrm{Ma}^{2}}{12}\)
Answer:
(a) \(\frac{\mathrm{Ma}^{2}}{6}\)
![]()
Question 106.
Moment of inertia of a rectangular plane sheet about an axis passing through center of mass and perpendicular to side b in its plane is –
(a) \(\frac{\mathrm{Ml}^{2}}{12}\)
(b) \(\frac{\mathrm{Ma}^{2}}{12}\)
(c) \(\frac{\mathrm{Mb}^{2}}{12}\)
(d) \(\frac{\mathrm{Ml}^{2}}{6}\)
Answer:
(c) \(\frac{\mathrm{Mb}^{2}}{12}\)
Question 107.
Rotational kinetic energy can be calculated by using –
(a) \(\frac{1}{2}\) I ω2
(b) \(\frac{\mathrm{L}^{2}}{2I}\)
(c) \(\frac{1}{2}\) Lω
(d) all the above
Answer:
(b) \(\frac{\mathrm{L}^{2}}{2I}\) )
Question 108.
The radius of gyration of a solid sphere of radius r about a certain axis is r. The distance of that axis from the center of the sphere is –
(a) \(\frac{2}{5}\)r
(b) \(\sqrt{\frac{2}{5}}\)r
(c) \(\sqrt{0.6r}\)
(d) \(\sqrt{\frac{5}{3}}\)
Answer:
(c) \(\sqrt{0.6r}\)
From parallel axis theorem
I = IG + Md2
mr2 = \(\frac{2}{5}\) mr2 + md2
d = \(\sqrt{\frac{3}{5}}\)r = \(\sqrt{0.6r}\)
Question 109.
A wheel is rotating with angular velocity 2 rad/s. It is subjected to a uniform angular acceleration 2 rad/s2 then the angular velocity after 10 s is
(a) 12 rad/s
(b) 20 rad/s
(c) 22 rad/s
(d) 120 rad/s
Answer:
(c) 22 rad/s
ω = ω0 + αt
Here ω0 = 2 rad/s,
α = 2 rad/s2
ω = 10 s
ω = 2 + 2 x 10 = 22 rad/s
![]()
Question 110.
Two rotating bodies A and B of masses m and 2m with moments of inertia IA and IB (Ib > IA) have equal kinetic energy of rotation. If LA and LB be their angular momenta respectively,
then,
(a) LB > LA
(b) LA > LB
(c) LA = \(\frac{L_{B}}{2}\)
(d) LA = 2LB
Answer:
(a) LB > LA
Question 111.
Three identical particles lie in x, y plane. The (x, y) coordinates of their positions are (3, 2), (1, 1), (5, 3) respectively. The (x, y) coordinates of the center of mass are –
(a) (a, b)
(b) (1, 2)
(c) (3, 2)
(d) (2, 1)
Answer:
(c) The X and Y coordinates of the center of mass are

Question 112.
A solid cylinder of mass 3 kg and radius 10 cm is rotating about its axis with a frequency of 20/π. The rotational kinetic energy of the cylinder
(a) 10 π J
(b) 12 J
(c) \(\frac{6 \times 10^{2}}{\pi}\) J
(d) 3 J
Answer:
(b) 12 J
Given,
M = 3 kg
R = 0.1 m
v = 20 / π
Angular frequency ω = 2πv = \(\frac{2π x 20}{π}\) = 40 rad/s-1
Moment of inertia of the cylinder about its axis = I = \(\frac{1}{2}\) mR2 = \(\frac{1}{2}\) x 3 x (0.1)2 = 0.015 kg m2
K.E. = \(\frac{1}{2}\) Iω2 = \(\frac{1}{2}\) x 0.015 x (40)2 = 12 J
Question 113.
A circular disc is rolling down in an inclined plane without slipping. The percentage of rotational energy in its total energy is
(a) 66.61%
(b) 33.33%
(c) 22.22%
(d) 50%
Answer:
(b) 33.33%
Rotational K.E. = \(\frac{1}{2}\)Iω2 \(\frac{1}{2}\)(\(\frac{1}{2}\)MR2)ω2 = \(\frac{1}{4}\) MR2ω2
Transnational K.E. = \(\frac{1}{2}\)MV2 = \(\frac{1}{2}\)M(Rω)2 = \(\frac{1}{2}\) MR2ω2
Total kinetic energy = Erot + Etrans = \(\frac{1}{4}\) MR2ω2\(\frac{1}{2}\)M(Rω)2 = \(\frac{3}{4}\) MR2ω2
% of Erot = \(\frac{E_{\text {rot }}}{E_{\text {Tot }}}\) x 100% = 33.33%
![]()
Question 114.
A sphere rolls down in an inclined plane without slipping. The percentage of transnational energy in its total energy is
(a) 29.6%
(b) 33.4%
(c) 71.4%
(d) 50%
Answer:
(c) 71.4%
Rotational K.e. Erot =
![]()

Question 115.
Two blocks of masses 10 kg and 4 kg are connected by a spring of negligible mass and placed on a frictionless horizontal surface. An impulse gives a velocity of 14 m/s to the heavier block in the direction of the lighter block. The velocity of the center of mass is –
(a) 30 m/s
(b) 20 m/s
(c) 10 m/s
(d) 5 m/s
Answer:
(c) According to law of conservation of linear momentum
MV = (M + M) VCM
VCM = \(\frac{MV}{M + M}\) = \(\frac{10 × 10}{10 + 4}\) = 10 ms-1
Question 116.
A mass is whirled in a circular path with constant angular velocity and its angular momentum is L. If the string is now halved keeping the angular velocity the same, the angular momentum is –
(a) \(\frac{L}{4}\)
(b) \(\frac{L}{2}\)
(c) L
(d) 2L
Answer:
(a) \(\frac{L}{4}\)
We know that
angular momentum L = Mr2
Here, m and co are constants L α r2
If r becomes \(\frac{r}{2}\) angular momentum becomes \(\frac{1}{4}\) th of its initial value.
Question 117.
The moment of inertia of a thin uniform ring of mass 1 kg and radius 20 cm rotating about the axis passing through the center and perpendicular to the plane of the ring is –
(a) 4 x 10-2 kg m2
(b) 1 x 10-2 kg m2
(c) 20 x 10-2 kg m2
(d) 10 x 10-2 kg m2
Answer:
(b) Moment of inertia I = MR2 = 1 x (10 x 10-2)2 = 1 x 10-2 kg m2.
![]()
Question 118.
A solid sphere is rolling down in the inclined plane, from rest without slipping. The angle of inclination with horizontal is 30°. The linear acceleration of the sphere is –
(a) 28 ms-2
(b) 3.9 ms-2
(c) \(\frac{25}{7}\)ms-2
(d) \(\frac{1}{20}\)ms-2
Answer:
(c) \(\frac{25}{7}\)ms-2
We know that,a =

Question 119.
An electron is revolving in an orbit of radius 2 A with a speed of 4 x 105 m /s. The angular momentum of the electron is [Me = 9 x 10-31 kg]
(a) 2 x 10-35 kg m2 s-1
(b) 72 x 10-36 kg m2 s-1
(c) 7.2 x 10-34 kg m2 s-1
(d) 0.72 x 10-37 kg m2 s-1
Answer:
(b) Angular momentum L = mV x r = 9 x 10-31 x 4 x 105 x 2 x 10-10 = 72 x 10-36kg m2 s-1
Question 120.
A raw egg and hard boiled egg are made to spin on a table with the same angular speed about the same axis. The ratio of the time taken by the eggs to stop is –
(a) =1
(b) < 1
(c) > 1
(d) none of these
Answer:
(d) When a raw egg spins, the fluid inside comes towards its side.
∴ “1” will increase in – turn it decreases ω. Therefore it takes lesser time than boiled egg.
∴\(\frac {time fìr raw egg}{time for boiled egg}\) < 1
Samacheer Kalvi 11th Physics Motion of System of Particles and Rigid Bodies Short Answer Questions (1 Mark)
Question 1.
What is a rigid body?
Answer:
A rigid body is the one which maintains its definite and fixed shape even when an external force acts on it.
Question 2.
When an object will have procession? Give one example.
Answer:
The torque about the axis will rotate the object about it and the torque perpendicular to the axis will turn the axis of rotation when both exist simultaneously on a rigid body the body will have a procession.
Example:
The spinning top when it is about to come to rest.
![]()
Question 3.
Define angular momentum. Give an expression for it.
Answer:
The angular momentum of a point mass is defined as the moment of its linear momentum.
\(\vec{L}\) = \(\vec{r}\) x \(\vec{p}\) or L = rp sin θ
Question 4.
When an angular momentum of the object will be zero?
Answer:
If the straight path of the particle passes through the origin, then the angular momentum is zero, which is also a constant.
Question 5.
When an object be in-mechanical equilibrium?
Answer:
A rigid body is said to be in mechanical equilibrium when both its linear momentum and angular momentum remain constant.
Question 6.
Derive an expression for the power delivered by torque.
Answer:
Power delivered is the work done per unit time. IF we differentiate the expression for work done with respect to time, we get the instantaneous
power (P).
p = \(\frac{dw}{dt}\) = τ \(\frac{dθ}{dt}\)
p = τ dω
Question 7.
A boy sits near the edge of revolving circular disc
- What will be the change in the motion of a disc?
- If the boy starts moving from edge to the center of the disc, what will happen?
Answer:
- As we know L = Iω = constant if the boy sits on the edge of revolving disc, its I will be increased in turn it reduces angular velocity.
- If the boy starts moving towards the center of the disc, its I will decrease in turn that increases its angular velocity.
Question 8.
Are moment of inertia and radius of gyration of a body constant quantities?
Answer:
No, moment of inertia and radius of gyration depends on axis of rotation and also on the distribution of mass of the body about its axis.
![]() .
.
Question 9.
A cat is able to land on its feet after a fall. Which principle of physics is being used? Explain.
Answer:
A cat is able to land on its feet after a fall. This is based on law of conservation of angular ~ momentum. When the cat is about to fall, it curls its body to decrease the moment of inertia and increase its angular velocity. When it lands it stretches out its limbs. By which it increases its moment of inertia and inturn it decreases its angular velocity. Hence, the cat lands safety.
Question 10.
About which axis a uniform cube will have minimum moment of inertia ?
Answer:
It will be about an axis passing through the center of the cube and connecting the opposite comers.
Question 11.
State the principle of moments of rotational equilibrium.
Answer:
∑ =\(\bar{\tau}\) = 0
Question 12.
Write down the moment of inertia of a disc of radius R and mass m about an axis in its plane at a distance R / 2 from its center.
Answer:
\(\frac { 1 }{ 2 }\) MR2
Question 13.
Can the couple acting on a rigid body produce translator motion ?
Answer:
No. It can produce only rotatory motion.
Question 14.
Which component of linear momentum does not contribute to angular momentum?
Answer:
Radial Component.
Question 15.
A system is in stable equilibrium. What can we say about its potential energy ?
Answer:
PE. is minimum.
Question 16.
Is radius of gyration a constant quantity ?
Answer:
No, it changes with the position of axis of rotation.
Question 17.
Two solid spheres of the same mass are made of metals of different densities. Which of them has a large moment of inertia about the diameter?
Answer:
Sphere of smaller density will have larger moment of inertia.
Question 18.
The moment of inertia of two rotating bodies A and B are IA and IB (IA > IB) and their angular momenta are equal. Which one has a greater kinetic energy ?
Answer:
K = \(\frac{\mathrm{L}^{2}}{2 \mathrm{I}}\) ⇒ KA > KA
Question 19.
A particle moves on a circular path with decreasing speed. What happens to its angular momentum?
Answer:
As \(\vec{L}\) = \(\vec{r}\) x m\(\vec{v}\) i.e., \(\vec{L}\) magnitude decreases but direction remains constant.
Question 20.
What is the value of instantaneous speed of the point of contact during pure rolling ?
Answer:
Zero.
Question 21.
Which physical quantity is conserved when a planet revolves around the sun ?
Answer:
Angular momentum of planet.
Question 22.
What is the value of torque on the planet due to the gravitational force of sun ?
Answer:
Zero.
Question 23.
If no external torque acts on a body, will its angular velocity be constant ?
Answer:
No.
![]()
Question 24.
Why there are two propellers in a helicopter ?
Answer:
Due to conservation of angular momentum.
Question 25.
A child sits stationary at one end of a long trolley moving uniformly with speed V on a smooth horizontal floor. If the child gets up and runs about on the trolley in any manner, then what is the effect of the speed of the centre of mass of the (trolley + child) system ?
Answer:
No change in speed of system as no external force is working.
Samacheer Kalvi 11th Physics Motion of System of Particles and Rigid Bodies Short Answer Questions (2 Marks)
Question 26.
State the factors on which the moment of inertia of a body depends.
Answer:
- Mass of body
- Size and shape of body
- Mass distribution w.r.t. axis of rotation
- Position and orientation of rotational axis
Question 27.
On what factors does radius of gyration of body depend?
Answer:
Mass distribution.
Question 28.
Why the speed of whirl wind in a Tornado is alarmingly high?
Answer:
In this, air from nearly regions get concentrated in a small space, so I decreases considerably. Since Iω = constant so ω increases so high.
Question 29.
Can a body be in equilibrium while in motion? If yes, give an example.
Answer:
Yes, if body has no linear and angular acceleration then a body in uniform straight line of motion will be in equilibrium.
Question 30.
There is a stick half of which is wooden and half is of steel, (i) it is pivoted at the wooden end and a force is applied at the steel end at right angle to its length (ii) it is pivoted at the steel end and the same force is applied at the wooden end. In which case is the angular acceleration more and why?
Answer:
I (first case) > 1 (Second case)
∴ τ r = l α
⇒ α (first case) < α (second case)
![]()
Question 31.
If earth contracts to half of its present radius what would be the length of the day at equator?
Answer:

Question 32.
An internal force cannot change the state of motion of center of mass of a body. Flow does the internal force of the brakes bring a vehicle to rest?
Answer:
In this case the force which bring the vehicle to rest is friction, and it is an external force.
Question 33.
When does a rigid body said to be in equilibrium? State the necessary condition for a body to be in equilibrium.
Answer:
For translation equilibrium
∑ Fext = 0
For rotational equilibrium
∑ \(\overline{\mathrm{τ}}\)ext = 0
Question 34.
How will you distinguish between a hard boiled egg and a raw egg by spinning it on a table top’
Answer:
For same external torque, angular acceleration of raw egg will be small than that of Hard boiled egg.
Question 35.
Equal torques are applied on a cylinder and a sphere. Both have same mass and radius. Cylinder rotates about its axis and sphere rotates about one of its diameter. Which will acquire greater speed and why?
Answer:
τ = I α α = \(\frac { τ }{ I }\)
α in cylinder, αC = \(\frac{\tau}{I_{C}}\)
α in sphere, αS = \(\frac{\tau}{I_{S}}\)
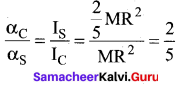
Question 36.
In which condition a body lying in gravitational field is in stable equilibrium?
Answer:
When vertical line through center of gravity passes through the base of the body.
![]()
Question 37.
Give the physical significance of moment of inertia. Explain the need of fly wheel in Engine.
Answer:
It plays the same role in rotatory motion as the mass does in translator y motion.
Samacheer Kalvi 11th Physics Motion of System of Particles and Rigid Bodies Short Answer Questions (3 Marks)
Question 38.
Three mass point m1, m2, m3 are located at the vertices of equilateral A of side ‘a’. What is the moment of inertia of system about an axis along the altitude of A passing through mi?
Answer:

Question 39.
A disc rotating about its axis with angular speed ω0 is placed lightly (without any linear push) on a perfectly friction less table. The radius of the disc is R. What are the linear velocities of the points A, B and C on the disc shown in figure. Will the disc roll?
Answer:
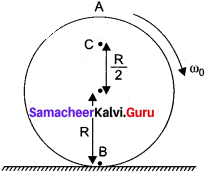
For A VA = R ω0 in forward direction
For B = VB = R ω0 in backward direction R
For C, VC = \(\frac {R}{2}\) ω0 in forward direction disc will not roll.
Question 40.
Find the torque of a force 7\(\hat{i}\) – 3\(\hat{j}\) – 5\(\hat{k}\) about the origin which acts on a particle whose position vector is \(\hat{j}\) +\(\hat{j}\) – \(\hat{j}\)
Answer:

Samacheer Kalvi 11th Physics Motion of System of Particles and Rigid Bodies Numericals
Question 41.
Three masses 3 kg, 4 kg and 5 kg are located at the comers of an equilateral triangle of side 1 m. Locate the center of mass of the system.
Answer:
(x,y) = (0.54 m, 0.36 m)
Question 42.
Two particles mass 100 g and 300 g at a given time have velocities 10\(\hat{j}\) – 7\(\hat{j}\) – 3\(\hat{j}\) and 7\(\hat{i}\) – 9 \(\hat{j}\) + 6\(\hat{k}\) ms-1 respectively. Determine velocity of center of mass.
Answer:
Velocity of center of mass = \(\frac{31 \hat{i}-34 \hat{j}+15 \hat{k}}{2}\) ms-1
![]()
Question 43.
From a uniform disc of radius R, a circular disc of radius R / 2 is cut out. The center of the hole is at R / 2 from the center of original disc. Locate the center of gravity of the resultant flat body.
Answer:
Center of mass of resulting portion lies at R/6 from the center of the original disc in a direction opposite to the center of the cut out portion.
Question 44.
The angular speed of a motor wheel is increased from 1200 rpm to 3120 rpm in 16 seconds,
- What is its angular acceleration (assume the acceleration to be uniform)
- How many revolutions does the wheel make during this time ?
Answer:
a = 4π rad s-2
n = 576
Question 45.
A meter stick is balanced on a knife edge at its center. When two coins, each of mass 5 g are put one on top of the other at the 12.0 cm mark, the stick is found to be balanced at 45.0 cm, what is the mass of the meter stick?
Answer:
m = 66.0 gm.
Question 46.
A solid sphere is rolling op a friction less plane surface about its axis of symmetry. Find ratio of its rotational energy to its total energy.
Answer:

Question 47.
Calculate the ratio of radii of gyration of a circular ring and a disc of the same radius with respect to the axis passing through their centers and perpendicular to their planes.
Answer:
2 : 1
Question 48.
Two discs of moments of inertia I1 and I2 about their respective axes (normal to the disc and passing through the center), and rotating with angular speed col and ω2 are brought into contact face to face with their axes of rotation coincident,
- What is the angular speed of the two – disc system ?
- Show that the kinetic energy of the combined system is less than the sum of the initial kinetic energies of the two discs. How do you account for this loss in energy ? Take ω1 ≠ ω2.
Answer:
- Let co be the angular speed of the two-disc system. Then by conservation of angular momentum
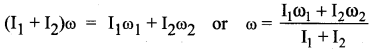
- Initial K.E. of the two discs.

Hence there is a loss of rotational K.E. which appears as heat.
When the two discs are brought together, work is done against friction between the two discs.
Question 49.
In the HCL molecule, the separating between the nuclei of the two atoms is about 1.27 Å (1Å = 10-10m). Find the approximate location of the CM of the molecule, given that the chlorine atom is about 35.5 times as massive as a hydrogen atom and nearly all the mass of an atom is concentrated in all its nucleus.
Answer:
As shown in Fig. suppose the H nucleus is located at the origin. Then,
x1 = 0, x2 = 1.27 Å, m1 = 1, m2 = 35.5
The position of the CM of HCl molecule is
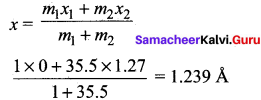
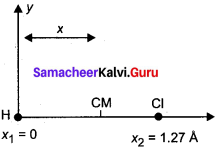
Thus the CM of HCl is located on the line joining H and Cl nuclei at a distance of 1.235 Å from the H nucleus.
Question 50.
A child stands at the center of turn table with his two arms out stretched. The turn table is set rotating with an angular speed of 40 rpm. How much is the angular speed of the child if he folds his hands back and thereby reduces his moment of inertia to 2/3 times the initial value?
- Assume that the turn table rotates without friction
- Show that the child’s new kinetic energy of rotation is more than the initial kinetic energy of rotation.
How do you account for this increase in kinetic energy ?
Answer:
Here ω = 40 rpm, I2 = \(\frac { 1 }{ 2 }\) I1
By the principle of conservation of angular momentum,
I1ω1 = I2ω2 or I1 x 4o = \(\frac {2}{5}\) I1 ω1 or ω2 = 100 rpm
(ii) Initial kinetic energy of rotation –
![]()
new kinetic energy of rotation –
Thus the child’s new kinetic energy of rotation is 2.5 times its initial kinetic energy of rotation. This increase in kinetic energy is due to the internal energy of the child which he uses in folding his hands back from the out stretched position.
![]()
Question 51.
To maintain a rotor at a uniform angular speed of 200 rad s-1 an engine needs to transmit a torque of 180 N m. What is the power required by the engine? Assume that the engine is 100% efficient.
Here ω = 200 rad s-1, τ = 180 N m
Power, P = τω = 180 x 200 = 36,000 W = 36 kW.
Question 52.
A car weighs 1800 kg. The distance between its front and back axles is 1.8 m. Its center of gravity is 1.05 m behind the front axle. Determine the force exerted by the level ground on each front and back wheel.
Answer:
For transnational equilibrium of car
NF + NB = W = 1800 x 9.8 = 17640 N
For rotational equilibrium of car
1.05 NF = 0.75 NB
1.05 NF = 0.75(17640 – NF )
1.8 NF = 13230
NF = 13230 / 1.8 = 7350 N
NB = 17640 – 7350 = 10290 N
Force on each front wheel = \(\frac {7350}{ 2 }\) = 3675 N
Force on each back wheel = \(\frac {10290}{ 2 }\) = 5145 N
Samacheer Kalvi 11th Physics Motion of System of Particles and Rigid Bodies Long Answer Questions (5 Marks)
Question 1.
Derive an expression for center of mass for distributed point masses.
Answer:
A point mass is a hypothetical point particle which has nonzero mass and no size or shape. To find the center of mass for a collection of n point masses, say,m1 , m2, m3 ….. mn we have to first choose an origin and an appropriate coordinate system as shown in Figure. Let, x1, x2, x3 …….. xn be the X – coordinates of the positions of these point masses in the X direction from the origin.
The equation for the X coordinate of the center of mass is,
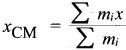
where, ∑ mi ¡s the total mass M of all the particles. ( ∑ mi = M).Hence,
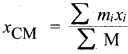
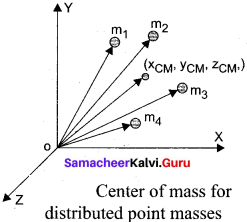
Similarly, we can also find y and z coordinates of the center of mass for these distributed point masses as indicated in figure.
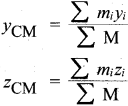
Hence, the position of center of mass of these point masses in a Cartesian coordinate system is (xCM, yCM zCM). in general, the position of center of mass can be written in a vector form as,
![]()
where, is the position vector of the center of mass and \(\vec{r}_{i}\) = xi \(\hat{j}\) + yi\(\hat{j}\) + zi\(\hat{k}\) is the position vector of the distributed point mass; where, \(\hat{i}\), \(\hat{j}\), and \(\hat{j}\) are the unit vectors along X, Y and Z-axis respectively.
Question 2.
Discuss the center of mass of two point masses with pictorial representation.
Answer:
With the equations for center of mass, let us find the center of mass of two point masses m1 and m2, which are at positions x1 and x2 respectively on the X – axis. For this case, we can express the position of center of mass in the following three ways based on the choice of the coordinate system.
![]()
(1) When the masses are on positive X-axis:
The origin is taken arbitrarily so that the masses m1 and m2 are at positions x1 and x2 on the positive X-axis as shown in figure (a). The center of mass will also be on the positive X- axis at xCM as given by the equation,
\(x_{\mathrm{CM}}=\frac{m_{1} x_{1}+m_{2} x_{2}}{m_{1}+m_{2}}\)
(2) When the origin coincides with any one of the masses:
The calculation could be minimized if the origin of the coordinate system is made to coincide with any one of the masses as shown in figure (b). When the origin coincides with the point
mass m1, its position x1 is zero, (i.e. x1 = 0). Then,
\(x_{\mathrm{CM}}=\frac{m_{1}(0)+m_{2} x_{2}}{m_{1}+m_{2}}\)
The equation further simplifies as,
xCM = \(\frac{m_{2} x_{2}}{m_{1}+m_{2}}\)
(3) When the origin coincides with the center of mass itself:
If the origin of the coordinate system is made to coincide with the center of mass, then, xCM = O and the mass rn1 is found to be on the negative X- axis as shown in figure (c). Hence, its position x1 is negative, (i.e. – x1).
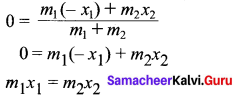
The equation given above is known as principle of moments.
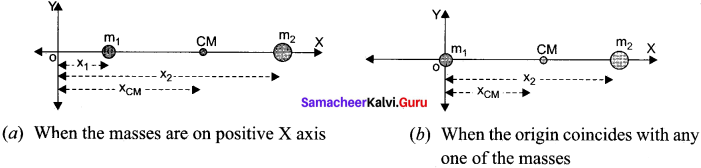
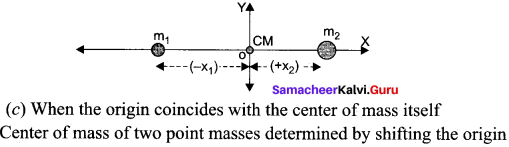
Question 3.
Derive an expression for kinetic energy in rotation and establish the relation between rotational kinetic energy and angular momentum.
Answer:
Let us consider a rigid body rotating with angular velocity ω about an axis as shown in figure. Every particle of the body will have the same angular velocity ω and different tangential velocities v based on its positions from the axis of rotation. Let us choose a particle of mass mi situated at distance ri from the axis of rotation. It has a tangential velocity vi given by the relation, vi = ri ω. The kinetic energy KEi. of the particle is,
KEi = \(\frac{1}{2} m_{i} v_{i}^{2}\)
Writing the expression with the angular velocity,
KE = \(\frac{1}{2}\) mi(riω)2 = \(\frac{1}{2} m_{i} r_{i}^{2}\)ω2
For the kinetic energy of the whole body, which is made up of large number of such particles, the equation is written with summation as,
KE = \(\frac{1}{2}\left(\sum m_{i} r_{i}^{2}\right)\)ω2
where, the term ∑ mirir is the moment of inertia I of the whole body. ∑ mirir
Hence, the expression for KE of the rigid body in rotational motion is –
KE = \(\frac{1}{2}\) Iω2
This is analogous to the expression for kinetic energy in transnational motion.
KE = \(\frac{1}{2}\) Mv2
Relation between rotational kinetic energy and angular momentum
Let a rigid body of moment of inertia I rotate with angular velocity ω.
The angular momentum of a rigid body is, L = Iω
The rotational kinetic energy of the rigid body is, KE = \(\frac{1}{2}\) Iω2
By multiplying the numerator and denominator of the above equation with I, we get a relation between L and KE as,
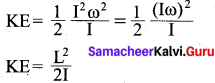
Question 4.
Discuss how the rolling is the combination of transnational and rotational and also be possibilities of velocity of different points in pure rolling.
Answer:
The rolling motion is the most commonly observed motion in daily life. The motion of wheel is an example of rolling motion. Round objects like ring, disc, sphere etc. are most suitable for rolling. Let us study the rolling of a disc on a horizontal surface. Consider a point P on the edge of the disc. While rolling, the point undergoes transnational motion along with its center of mass and rotational motion with respect to its center of mass.
Combination of Translation and Rotation:
We will now see how these transnational and rotational motions arc related in rolling. If the radius of the rolling object is R, in one full rotation, the center of mass is displaced by 2πR (its circumference). One would agree that not only the center of mass. but all the points Of l the disc are displaced by the same 2πR after one full rotation. The only difference is that the center of mass takes a straight path; but, all the other points undergo a path which has a combination of the transnational and rotational motion. Especially the point on the edge undergoes a path of a cyclonic as shown in the figure.
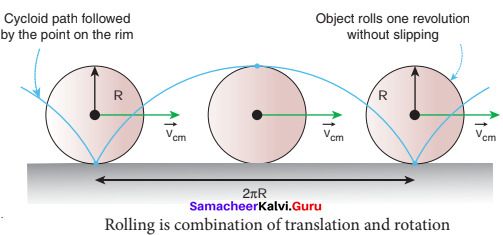
As the center of mass takes only a straight line path. its velocity vCM is only transnational velocity vTRANS (vCM = vTRANS). All the other points have two velocities. One is the transnational velocity vTRANS (which is also the velocity of center of mass) and the other is the rotational velocity vROT (vROT = rω). Here, r ¡s the distance of the point from the center of mass and o is the angular velocity. The rotational velocity vROT is perpendicular to the instantaneous position vector from the center of mass as shown in figure (a). The resultant of these two velocities is v. This resultant velocity y is perpendicular to the position vector from the point of contact of the rolling object with the surface on which it is rolling as shown in figure (b).
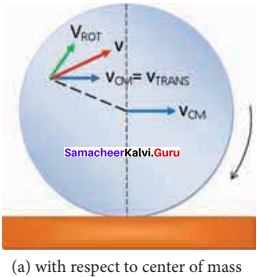
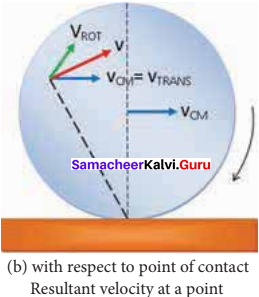
We shall now give importance to the point of contact. In pure rolling, the point of the rolling object which comes in contact with the surface is at momentary rest. This is the case with every point that is on the edge of the rolling object. As the rolling proceeds, all’the points on the edge, one by one come in contact with the surface; remain at momentary rest at the time of contact and then take the path of the cycloid as already mentioned.
Hence, we can consider the pure rolling in two different ways.
(i) The combination of transnational motion and rotational motion about the center of mass.
(or)
(ii) The momentary rotational motion about the point of contact.
As the point of contact is at momentary rest in pure rolling, its resultant velocity v is zero (v = o). For example, in figure, at the point of contact, vTRANS is forward (to right) and vROT is backwards (to the left).
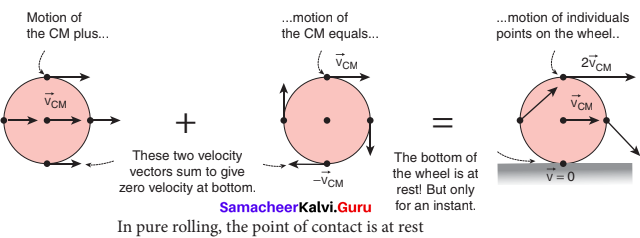
That implies that, vTRANS and vROT are equal in magnitude and opposite in direction (v = vTRANS – vROT = 0). Hence, we conclude that in pure rolling, for all the points on the edge, the magnitudes of vTRANS and vROT are equal (vTRANS = vROT) As vTRANS = vCM and vROT = Rω, in pure rolling we have,
vCM = Rω
We should remember the special feature of the above equation. In rotational motion, as per the relation v = rω, the center point will not have any velocity as r is zero. But in rolling motion, it suggests that the center point has a velocity vCM given by above equation vCM – Rω. For the topmost point, the two velocities vTRANS and vROT are equal in magnitude and in the same direction (to the right). Thus, the resultant velocity v is the sum of these two velocities, v = vTRANS + vROT In other form, v = 2 vCM as shown in figure below.
![]()
Question 5.
Derive an expression for kinetic energy in pure rolling.
Answer:
As pure is the combination of transnational and rotational motion, we can write the total kinetic energy (KE) as the sum of kinetic energy due to transnational motion (KETRANS) and kinetic energy due to rotational motion (KEROT).
KE = KETRANS + KEROT ………(i)
If the mass of the rolling object is M, the velocity of center of mass is vCM, its moment of inertia about center of mass is ICM and angular velocity is ω, then
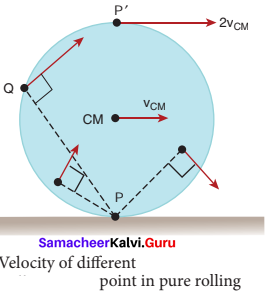
With center of mass as reference:
The moment of inertia (ICM) of a rolling object about the center of mass is, ICM = MK2 and vCM = Rω. Here, K is radius of gyration.

With point of contact as reference:
We can also arrive at the same expression by taking the momentary rotation happening with respect to the point of contact (another approach to rolling). If we take the point of contact as o, then,
KE = \(\frac {1}{2}\) I0ω2
Here, I0 is the moment of inertia of the object about the point of contact. By parallel axis
theorem, I0 = ICM + MK2 Further we can write, I0 MK2 + MR2. With vCM = Rω or ω = \(\frac{v_{\mathrm{CM}}}{\mathrm{R}}\)

As the two equations (v) and (vi) are the same, it ¡s once again confirmed that the pure tolling problems could be solved by considering the motion as any one of the following two cases.
(i) The combination of transnational motion and rotational motion about the center of mass.
(or)
(ii) The momentary rotational motion about the point of contact.
Question 6.
- Can a body in translator y motion have angular momentum? Explain.
- Why is it more difficult to revolve a stone by tying it to a longer string than by tying it to a shorter string?
Answer:
(1) Yes, a body in translatory motion shall have angular momentum unless fixed point about which angular momentum is taken lies on the line of motion of body
\(|\overrightarrow{\mathrm{L}}|\) = rp sin θ
= 0 only when θ = O° or 180°
(2) MI of stone I = ml2 (l – length of string) l is large, a is very small
τ = Iα
α = \(\frac {τ}{I}\) = \(\frac{\tau}{m l^{2}}\)
if l is large a is very small.
∴ more difficult to revolve.
![]()