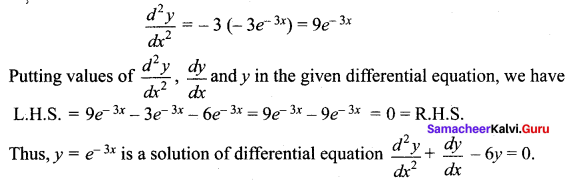Samacheer Kalvi 12th Maths Solutions Chapter 10 Ordinary Differential Equations Ex 10.4

You can Download Samacheer Kalvi 12th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 10 Ordinary Differential Equations Ex 10.4

Question 1.
Show that each of the following expressions is a solution of the corresponding given differential equation.
(i) y = 2x² ; xy’ = 2y
Solution:
y = 2x‘; xy’ = 2y
Given y = 2x²
Differentiating with respect to ‘x’, we get
\(\frac { dy }{ dx }\) = 2.2 x
multiply by x on both sides, we get
x\(\frac { dy }{ dx }\) = 2.2 x²
xy’ = 2y is a given differential equation.
Thus y = 2x² satisfies the differential equation
xy’ = 2y
Hence y = 2x² is a solution of the differential equation xy’ = 2y

(ii) y = ae^x + be^-x ; y” – y = 0
Solution:
Given y = ae^x + be^-x
differentiating with respect to x, we get
\(\frac { dy }{ dx }\) = ae^x – be^-x [∵ \(\frac { d }{ dx }\) e^-x = e^-x (-1)]
Again differentiating, we get
\(\frac { d^2y }{ dx^2 }\) = ae^x + be^-x
\(\frac { d^2y }{ dx^2 }\) = y
\(\frac { d^2y }{ dx^2 }\) – y = 0 is a required differential equation.
Thus y = ae^x + be^-x satisfies the differential equation y”- y = 0.
Hence y = ae^x + be^-x is a solution of the differential I equation y” – y = 0

Question 2.
Find the value of m so that the function y = e^mx is a solution of the given differential equation.
(i) y + 2y = 0
Solution:
Given solution y = e^mx
Differentiate with respect to ‘x’

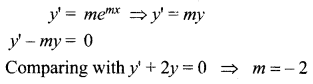
(ii) y” – 5y’ + 6y = 0

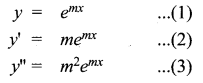
Given differential equation is y” – 5y’ + 6y = 0
Substitute (1), (2) and (3) in this

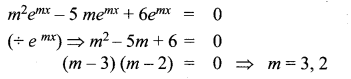
Question 3.
The slope of the tangent to the curve at any point is the reciprocal of four times the ordinate at that point. The curve passes through (2, 5). Find the equation of the curve.
Solution:
The slope of the tangent is the reciprocal of four times the ordinate

Question 4.

Solution:

Question 5.
Show that y = ax + \(\frac{b}{x}\), x ≠ 0, is a solution of the differential equation x²y”+ xy’ – y = 0.
Solution:

Here ‘a’ and ‘b’ are arbitrary constants

Differentiate with respect to ‘x’
xy’ + y . 1 = a (2x) = 2ax ……….. (2)
Differentiate again with respect to ‘x’ .
xy” + y’ . 1 + y = 2a ⇒ xy” + 2y’ = 2a …….. (3)
Substitute (3) in (2)
xy’ + y = (xy” + 2y’)x
xy’ + y = x²y” + 2xy’ ⇒ x²y” + xy’ – y = 0
Hence proved.

Question 6.
Show that y = ae^-3x + b, where a and b are arbitrary constants, is a solution of the differential equation

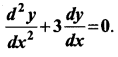
Solution:

Question 7.
Show that the differential equation representing the family of curves 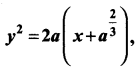where a is a positive parameter is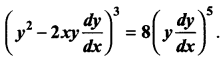
Solution:

Question 8.
Show that, y = a cos bx is a solution of the differential equation .
Solution:
y = a cos bx …(1) (a is an arbitrary constant)
Differentiating with respect to ‘x’

Again, differentiating with respect to ‘x’

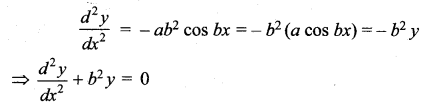
Hence proved

Samacheer Kalvi 12th Maths Solutions Chapter 10 Ordinary Differential Equations Ex 10.4 Additional Problems

Question 1.
Verify that the function y = a cos x + b sin x is a solution of the differential equation cos \(\frac{d y}{d x}\) + y sin x = b. dx
Solution:
The given function is y = a cos x + b sin x
Differentiating both sides with respect to x, we have

Putting values of \(\frac{d y}{d x}\) and y in the given differential equation, we have
L.H.S. = cos x (- a sin x + b cos x) + {a cos x + b sin x) sin x
= – a sin x cos x + b cos2 x + a sin x cos x + b sin2 x = b (cos2 x + sin2 x)
= b × 1 = b = R.H.S
Thus, y = a cos x + b sin x is a solution of differential equation

Question 2.
Verify that the function y = 4 sin 3x is a solution of the differential equation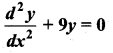
Solution:
The given function is y = 4 sin 3x
Differentiating both sides with respect to x, we have

Again, differentiating both sides with respect to x, we have

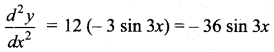
Putting values of \(\frac{d^{2} y}{d x^{2}}\) and y in the given differential equation, we have
L.H.S. = – 36 sin 3x + 9 (4 sin 3x) = – 36 sin 3x + 36 sin 3x = 0 = R.H.S.
Thus, y = 4 sin 3x is a solution of differential equation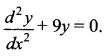

Question 3.
Verify that the function y = ax² + bx + c is a solution of the differential equation   .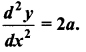
Solution:
The given function is y = ax² + bx + c
Differentiating both sides with respect to x, we have

Again differentiating both sides with respect to x, we have

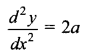
Which is the given differential equation.
Thus, y = ax² + bx + c is a solution of differential equation \(\frac{d^{2} y}{d x^{2}}\)= 2a.

Question 4.
Verify that the function y = e^-3x is a solution of the differential equation
Solution:
The given function is y = e^-3x
Differentiating both sides with respect to x, we have

Again, differentiating both sides with respect to x, we have