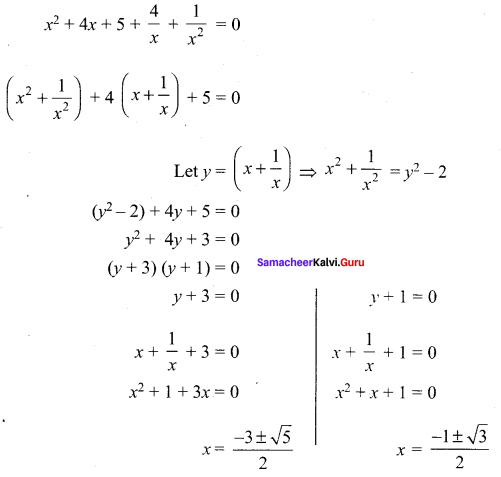You can Download Samacheer Kalvi 12th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 3 Theory of Equations Ex 3.5
Question 1.
Solve the following equations:
(i) sin2x – 5sinx + 4 = 0
(ii) 12x3 + 8x = 29x2 – 4
Solution:
(i) sin² x – 5 sin x + 4 = 0
Put sin x = t
t² – 5t + 4 = 0
(t – 1) (t – 4) = 0
t = 1 or t = 4
sin x = 4 or sin x = 1
(is not possible) sin x = sin \(\frac{π}{2}\)
x = nπ + (-1l)n \(\frac{π}{2}\) ∀ n ∈ z.
(ii) 12x3 + 8x = 29x2 – 4
12x3 – 29x2 + 8x + 4 = 0 ….. (1)
By Trail and error method, (x – 2) is a factor of (1)
The other factor is 12x2 – 5x – 2
The roots is 12x2 – 5x – 2 = 0
(3x – 2) (4x + 1) = 0
x = \(\frac{2}{3}\), x = \(-\frac{1}{4}\)
The roots are 2, \(\frac{2}{3}\), \(-\frac{1}{4}\)
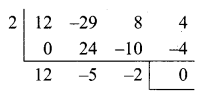
[Here an = 12, a0 = 4; Let \(\frac{p}{q}\) be the root of the equation (1)
The factors of a0 : ±1, ±2, ±4 (P must divisible by 4)
The factor of an : ±1, ±2, ±3, ±4, ±6, ±12
q must divide as (12)
Using these p and q we can form \(\pm 1, \pm 2, \pm \frac{1}{2}, \pm \frac{2}{3}, \pm \frac{1}{6}, \pm \frac{1}{4}, \pm \frac{3}{4}, \pm 3\) are the possible roots of equation. (1)]
Question 2.
Examine for the rational roots of:
(i) 2x3 – x2 – 1 = 0
(ii) x8 – 3x + 1 = 0
Solution:
(i) 2x3 – x2 – 1 = 0
Sum of the co-efficients = 0
∴ (x – 1) is a factor
The other factor is 2x2 + x + 1.
The root is (2x2 + x + 1) = 0
Here ∆ = b2 – 4ac = (1)2 – 4(2) (1) = 1 – 8 = -7 < 0
The remaining roots are imaginary.
The only rational root is x = 1
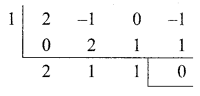
(ii) x8 – 3x + 1 = 0 …. (1)
Here an = 1, a0 = 1
If \(\frac{p}{q}\) is a rational root of (1)
Then q is a factor an, p is a factor of a0
The possible values of p and q are ± 1.
Among the possible values 1, -1, [(p, q) = 1]
None of them satisfies the equation (1)
The above equation has no rational roots.
![]()
Question 3.
Solve: \(8 x^{\frac{3}{2 n}}-8 x^{\frac{-3}{2 n}}=63\)
Solution:

Squaring on both sides
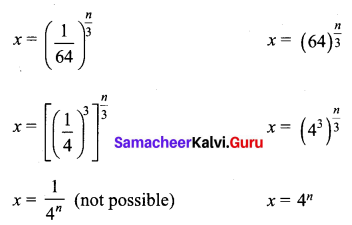
only possible solution is x = 4n
Question 4.
Solve: \(2 \sqrt{\frac{x}{a}}+3 \sqrt{\frac{a}{x}}=\frac{b}{a}+\frac{6 a}{b}\)
Solution:


Question 5.
Solve the equations:
(i) 6x4 – 35x3 + 62x2 – 35x + 6 = 0
(ii) x4 + 3x3 – 3x – 1 = 0
Solution:
(i) 6x4 – 35x3 + 62x2 – 35x + 6 = 0 ….. (1)
It is a even degree reciprocal equation as p(x) = \(x^{n} p\left(\frac{1}{x}\right)\)
Dividing equation (1) by x2,

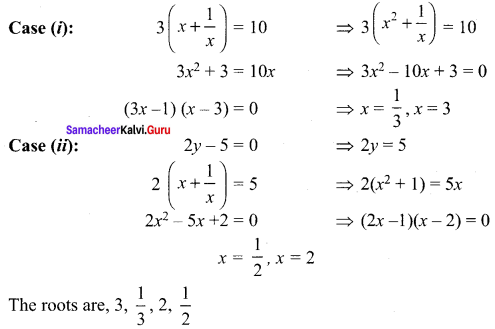
(ii) x4 + 3x3 – 3x – 1 = 0 …… (1)
It is an even degree reciprocal function of type II.
1, -1 are the solution of equation (1)
(x – 1), (x + 1) are the factor of (1)
(x2 – 1) is a factor of (1)
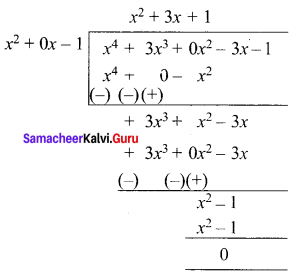
Dividing (1) by (x2 – 1)
we get, x2 + 3x + 1 = 0 is the other factor.
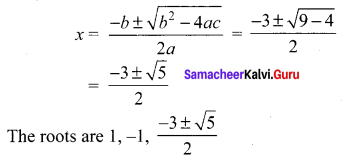
Question 6.
Find all real numbers satisfying 4x – 3(2x+2) + 25 = 0
Solution:
4x – 3(2x+2) + 25 = 0.
(2x)² – 3.(2x 2²) + 25 = 0
(2x)² – 12(2x) + 32 = 0
Put 2x = t
(t² – 12t + 32 = 0)
(y – 4)(y – 8) = 0
y = 4 or y = 8
t = 8 (or) t = 4
2x = 8 = 2³ (or) 2x = 4 = (2)²
x = 3 (or) x = 2
Roots are 3, 2
![]()
Question 7.
Solve the equation 6x4 – 5x3 – 38x2 – 5x + 6 = 0 if it is known that \(\frac{1}{3}\) is a solution.
Solution:
6x4 – 5x3 – 38x2 – 5x + 6 = 0 …… (1)
x = \(\frac{1}{3}\) is a Solution
∴ (3x – 1) is a factor of (1)
(1) is a Reciprocal equation even degree divide (1) by x2.


Samacheer Kalvi 12th Maths Solutions Chapter 3 Theory of Equations Ex 3.5 Additional Problems
Question 1.
Solve: 32x + 4 + 1 = 2.3x + 2
Solution:
32x + 4 = 3x + 2 + 3x + 2 – 1
32x + 4 – 3x + 2 = 3x + 2 – 1 ⇒ 3x + 2[3x + 2 – 1] = [3x + 2 – 1]
3x + 2= 1 ⇒ 3x + 2 = 30
x + 2 = 0 ⇒ x = -2
Question 2.
Solve: 2x – 2x + 3 + 24 = 0.
Solution:
22x – (2x.23) + 24 = 0 since 23 = 8 = 4 + 4 = 22 + 22
22x – (4 + 4)2x + 24 = 0 ⇒ 22x – (22 + 22)2x + 24 = 0
(2x – 22)(2x – 22) = 0 ⇒ (2x – 22)2 = 0
2x = 22 ⇒ x = 2
Question 3.
Solve: (x – 4) (x + 2) (x + 3) (x – 3) + 8 = 0.
Solution:
(x – 4) (x + 3) (x + 2) (x – 3) + 8 = 0
(x2 – x – 12) (x2 – x – 6) + 8 = 0
Let y = x2 – x
(y – 12) (y – 6) + 8 = 0 ⇒ y2 – 18y + 72 + 8 = 0
y2 – 18y + 80 = 0 ⇒ (y – 10)( y – 8) = 0
Case (i) y – 10 = 0
x2 – x – 8 = 0
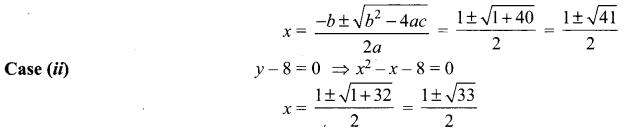
Question 4.
![]()
Solution:

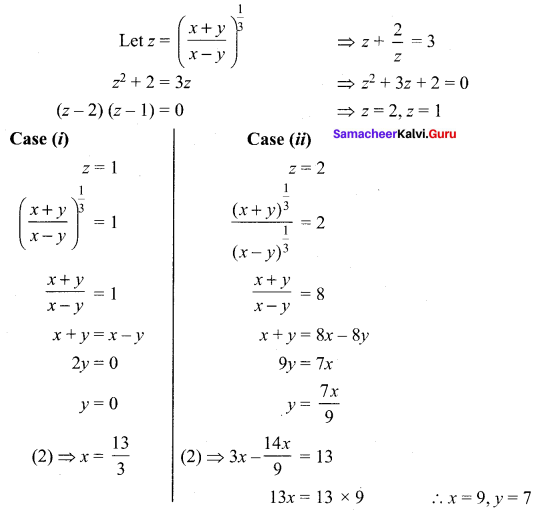
Question 5.
5x – 1 + 51 – x = 26
Solution:

![]()
Question 6.
Solve: 12x4 – 56x3 + 89x2 – 56x + 12 = 0
Solution:
Since the coefficients of the equations are equal from both ends.
Divide the equation by x2
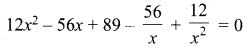
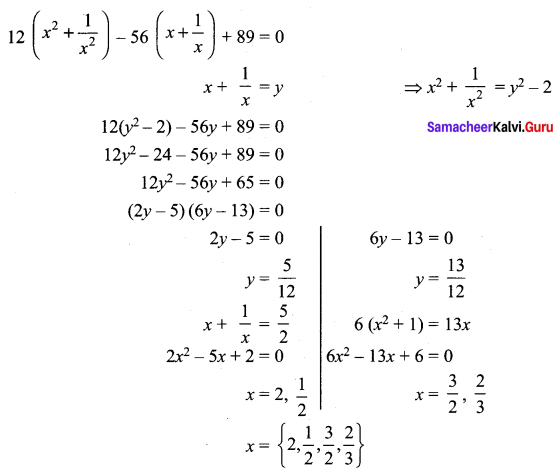
Question 7.
![]()
Solution:

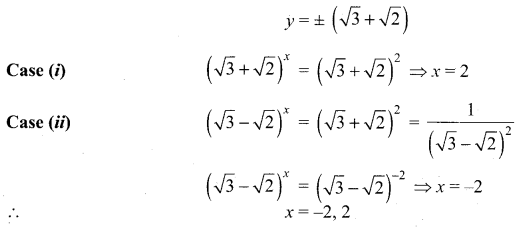
Question 8.
Solve: x4 + 4x3 + 5x2 + 4x + 1 = 0
Solution: