You can Download Samacheer Kalvi 12th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 1 Applications of Matrices and Determinants Ex 1.6
Question 1.
Test for consistency and if possible, solve the following systems of equations by rank method.
(i) x – y + 2z = 2, 2x + y + 4z = 7, 4x – y + z = 4
(ii) 3x + y + z = 2, x – 3y + 2z = 1, 7x – y + 4z = 5
(iii) 2x + 2y + z = 5, x – y + z = 1, 3x + y + 2z = 4
(iv) 2x – y + z = 2, 6x – 3y + 3z = 6, 4x – 2y + 2z = 4
Solution:
(i) Here the number of unknowns = 3.
The matrix form of the system is AX = B where
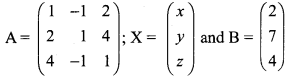
(i.e) AX = B
The augmented matrix (A, B) is
\((\mathrm{A}, \mathrm{B})=\left(\begin{array}{cccc}{1} & {-1} & {2} & {2} \\ {2} & {1} & {4} & {7} \\ {4} & {-1} & {1} & {4}\end{array}\right)\)
Applying Gaussian elimination method on [A,B] we get

The above matrix is in echelon form also ρ(A, B) = ρ(A) = 3 = number of unknowns
The system of equations is consistent with a unique solution. To find the solution.
Now writing the equivalent equations we get
\(\left(\begin{array}{ccc}{1} & {-1} & {2} \\ {0} & {3} & {0} \\ {0} & {0} & {-7}\end{array}\right)\left(\begin{array}{l}{x} \\ {y} \\ {z}\end{array}\right)=\left(\begin{array}{r}{2} \\ {3} \\ {-7}\end{array}\right)\)
x – y + 2z = 2
3y = 3 ⇒ y = 1
7z = -7 ⇒ z = 1
Substituting z = y = 1 in (1) we get
x – 1 + 2 = 2 ⇒ x = 1
⇒ x = y = z = 1
(ii) Here the number of unknowns is 3.
The matrix form of the given system of equations is:
\(\left(\begin{array}{ccc}{3} & {1} & {1} \\ {1} & {-3} & {2} \\ {7} & {-1} & {4}\end{array}\right)\left(\begin{array}{l}{x} \\ {y} \\ {z}\end{array}\right)=\left(\begin{array}{l}{2} \\ {1} \\ {5}\end{array}\right)\)
AX = B
(i.e) Now the augmented matrix [A, B] is

The above matrix is in echelon form also
ρ(A, B) = ρ(A) = 2< number of unknowns
The system of equations is consistent with the infinite number of solutions.
To find the solution:
Now writing the equivalent equations we get
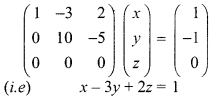

(iii) Here the number of unknowns is 3.
The matrix form of the given equation is
\(\left(\begin{array}{ccc}{2} & {2} & {1} \\ {1} & {-1} & {1} \\ {3} & {1} & {2}\end{array}\right)\left(\begin{array}{l}{x} \\ {y} \\ {z}\end{array}\right)=\left(\begin{array}{l}{5} \\ {1} \\ {4}\end{array}\right)\)
AX = B
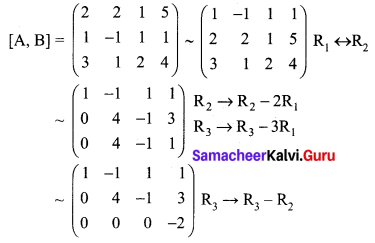
The above matrix is in echelon form.
Here ρ(A, B) = 3; ρ(A) = 2
So ρ(A, B) ≠ ρ(A)
The system of equations is inconsistent with no solution.
(iv) Here the number of unknowns is 3.
The matrix form of the given equation is
\(\left(\begin{array}{ccc}{2} & {-1} & {1} \\ {6} & {-3} & {3} \\ {4} & {-2} & {2}\end{array}\right)\left(\begin{array}{l}{x} \\ {y} \\ {z}\end{array}\right)=\left(\begin{array}{l}{2} \\ {6} \\ {4}\end{array}\right)\)
AX = B
The augmented matrix [A, B] is
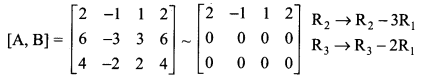
The above matrix is in echelon form also ρ(A, B) = ρ(A) = 1 < number of unknowns
The system of equations is consistent with the infinite number of solutions.
To find the Solution
Now writing the equivalent equations we get

![]()
Question 2.
Find the value of k for which the equations kx – 2y + z = 1, x – 2ky + z = -2, x – 2y + kz = 1 have
(i) no solution
(ii) unique solution
(iii) infinitely many solution
Solution:
The matrix form of the given system of equation is
\(\left(\begin{array}{ccc}{k} & {-2} & {1} \\ {1} & {-2 k} & {1} \\ {1} & {-2} & {k}\end{array}\right)\left(\begin{array}{l}{x} \\ {y} \\ {z}\end{array}\right)=\left(\begin{array}{c}{1} \\ {-2} \\ {1}\end{array}\right)\)
(i.e) AX = B
The augmented matrix (A, B) is

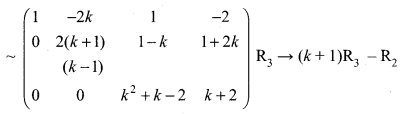
k2 + k – 2 = (k + 2) (k – 1)
The above matrix is in echelon form
Case 1: when k = 1, ρ(A, B) = 3, ρ(A) = 2 (i.e) ρ (A, B) ≠ ρ (A)
The system is inconsistent and the system has no solution.
Case 2: when k ≠ 1, k ≠ -2, then ρ(A, B) = ρ(A) = 3 = number of unknowns
The system is consistent with a unique solution.
Case 3: When k = -2 then ρ(A) = ρ(A, B) = 2 < number of unknowns.
The system is consistent with the infinite number of solutions.
Question 3.
Investigate the values of λ and µ the system of linear equations.
2x + 3y + 5z = 9, 7x + 3y – 5z = 8, 2x + 3y + λz = µ, have
(i) no solution
(ii) a unique solution
(iii) an infinite number of solutions.
Solution:
The matrix form of the above equation is
\(\left(\begin{array}{ccc}{2} & {3} & {5} \\ {7} & {3} & {-5} \\ {2} & {3} & {\lambda}\end{array}\right)\left(\begin{array}{l}{x} \\ {y} \\ {z}\end{array}\right)=\left(\begin{array}{l}{9} \\ {8} \\ {\mu}\end{array}\right)\)
(i.e) AX = B
The augmented matrix [A, B] is
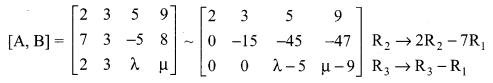
The above matrix is in echelon form
Case 1: When λ = 5, μ ≠ 9
ρ(A) = 2, ρ(A, B) = 3 (i.e) ρ(A, B) ≠ p(A)
The system is inconsistent and it has no solution.
Case 2: When λ ≠ 5, μ ∈ R,
ρ(A, B) = ρ(A) = 3 = number of unknowns
The system is consistent with a unique solution.
Case 3: When λ = 5, μ = 9,
then ρ(A, B) = ρ(A) = 2 < number of unknowns
The system is consistent with infinite number of solutions.
![]()
Samacheer Kalvi 12th Maths Solutions Chapter 1 Applications of Matrices and Determinants Ex 1.6 Additional Problems
Question 1.
Discuss the solutions of the system of equations for all values of λ.
x + y + z = 2,
2x + y – 2z = 2,
λx + y + 4z = 2
Solution:
The augmented matrix is

Case 1:
If λ ≠ 0, then we get ρ(A, B) = ρ(A) = 3 = number of unknowns.
∴ The system has unique solution.
Case 2: If λ = 0,then ρ(A, B) = ρ(A) = 2 < the number of unknowns ⇒ the system has more number of solutions. Taking λ = 0 we get the systems of equations as
x + 4z = 2 ……..(1)
2y – 6z = 0 …….. (2)
Taking z = k in (2), we get
2y – 6k = 0 ⇒ 2y = 6k
y = 3k
Taking z = A in (1) we get,
x + 4k = 2 ⇒ x = 2 – 4k
∴ The solution is x = 2 – 4 k, y = 3 k, z = k
Question 2.
For what values of k, the system of equations kx + y + z = 1, x + ky + z = 1, x + y + kz = 1 have
(i) unique solution,
(ii) more than one solution,
(iii) no solution.
Solution:
The augmented matrix is
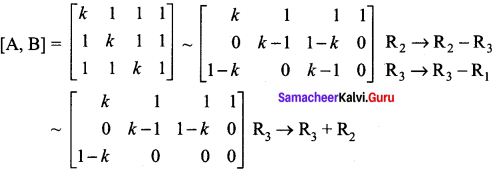
Case (i) : When k ≠ 1, the system has a unique solution
Case (ii) : When k = 1, the system reduces to a single equation x + y + z = 1. The system can have more than one solution.
Case (iii) : When k = -2, the system is inconsistent
∴ ρ(A, B) ≠ ρ(A); ∴ the system has no solution.