You can Download Samacheer Kalvi 11th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 3 Trigonometry Ex 3.10
Question 1.
Determine whether the following measurements produce one triangle, two triangles or no triangle:
∠B = 88°, a = 23, b = 2. Solve if solution exists.
Solution:
We are given a = 23,
b = 2, and
∠B = 88°.
So we can
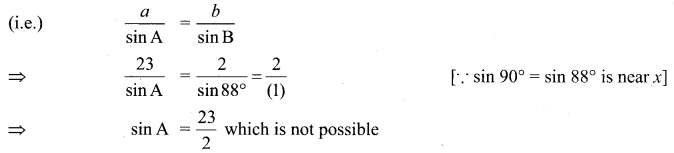
Question 2.
If the sides of a ∆ABC are a = 4, b = 6 and c = 8, then show that 4 cos B + 3 cos C = 2.
Solution:
a = 4,
b = 6,
c = 8
To prove 4 cos B + 3 cos C = 2

![]()
Question 3.
In a ∆ABC, if a = \(\sqrt{3}\) – 1, b = \(\sqrt{3}\) + 1 and C = 60°, find the other side and other two angles.
Solution:

Question 4.

Solution:
Question 5.
In a ∆ABC, if a = 12 cm, b = 8 cm and C = 30°, then show that its area is 24 sq.cm.
Solution:
a = 12 cm,
b = 8 cm,
C = 30°

Question 6.
In a ∆ABC, if a = 18 cm, b = 24 cm and c = 30 cm, then show that its area is 216 sq.cm.
Solution:
a = 18 cm,
b = 24 cm,
c = 30 cm
The sides form a right angled triangle
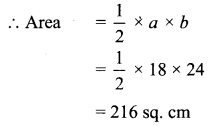
![]()
Question 7.
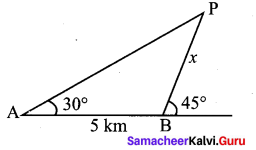
Two soldiers A and B in two different underground bunkers on a straight road, spot an intruder at the top of a hill. The angle of elevation of the intruder from A and B to the ground level in the eastern direction are 30° and 45° respectively. If A and B stand 5 km apart, find the distance of the intruder from B.
Solution:
By using sine formula
\(\frac{x}{\sin 30^{\circ}}=\frac{5}{\sin 15^{\circ}}\)
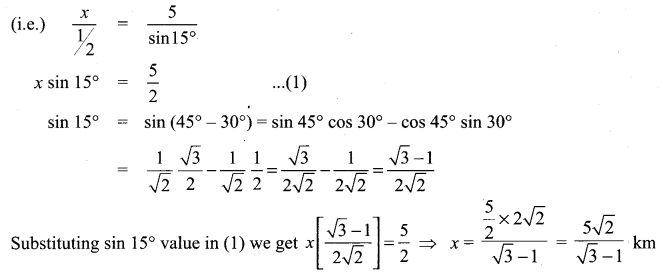
Question 8.
A researcher wants to determine the width of a pond from east to west, which cannot be done by actual measurement. From a point P, he finds the distance to the eastern-most point of the pond to be 8 km, while the distance to the western most point from P to be 6 km. If the angle between the two lines of sight is 60°, find the width of the pond.
Solution:
p2 = W2 + E2 – 2WE cos P
P2 = 64 + 36 – 2 × 8 × 6 × Cos 60°
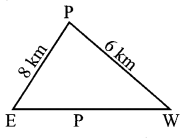
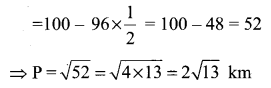
Question 9.
Two Navy helicopters A and B are flying over the Bay of Bengal at same altitude from the sea level to search a missing boat. Pilots of both the helicopters sight the boat at the same time while they are apart 10 km from each other. If the distance of the boat from A is 6 km and if the line segment AB subtends 60° at the boat, find the distance of the boat from B.
Solution:

Question 10.
A straight tunnel is to be made through a mountain. A surveyor observes the two extremities A and B of the tunnel to be built from a point P in front of the mountain. If AP = 3 km, BP = 5 km and ∠APB = 120°, then find the length of the tunnel to be built.
Solution:
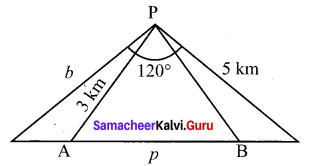
A, B are the two extremities of the tunnel.
P – Point of observation.
PA , PB are the directions of the points A, B as observed from the point P
AP = 3 km, BP = 5 km, ∠ APB = 120°
Using cosine formula in ∆ APB
AB2 = AP2 + BP2 – 2AP. BP. cos(120°)
AB2 = 32 + 52 – 2 × 3 × 5 cos (180° – 60°)
= 9 + 25 – 30 (- cos 60°)
= 34 + 30 × \(\frac { 1 }{ 2 }\)
= 34 + 15 = 49
AB = √49 = 7
∴ The length of the tunnel AB = 7 k.m.
Question 11.
A farmer wants to purchase a triangular-shaped land with sides 120 feet and 60 feet and the angle included between these two sides is 60°. If the land costs ₹ 500 per sq. ft, find the amount he needed to purchase the land. Also, find the perimeter of the land.
Solution:
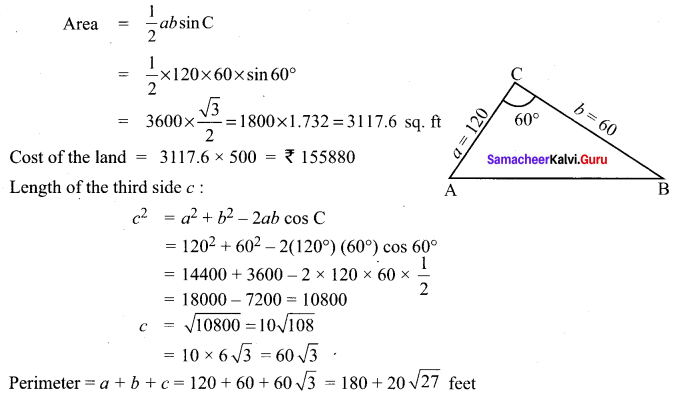
![]()
Question 12.
A fighter jet has to hit a small target by flying a horizontal distance. When the target is sighted, the pilot measures the angle of depression to be 30°. If after 100 km, the target has an angle of depression of 60°, how far is the target from the fighter jet at that instant?
Solution:
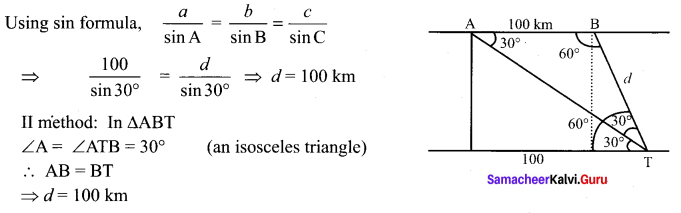
Question 13.
A plane is 1 km from one landmark and 2 km from another. From the plane’s point of view, the land between them subtends an angle of 60°. How far apart are the landmarks?
Solution:
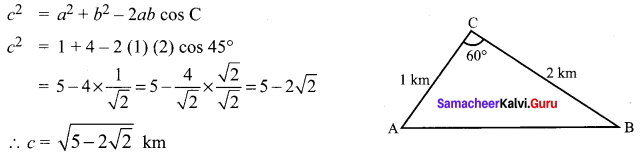
Question 14.
A man starts his morning walk at a point A reaches two points B and C and finally back to A such that ∠A= 60° and ∠B = 45°, AC = 4 km in the ∆ABC. Find the total distance he covered during his morning walk.
Solution:

![]()
Question 15.
Two vehicles leave the same place P at the same time moving along two different roads. One vehicle moves at an average speed of 60 km/hr and the other vehicle moves at an average speed of 80 km/hr. After half an hour the vehicle reaches destinations A and B. If AB subtends 60° at the initial point P, then find AB.
Solution:

= 900+ 1600 – 1200 = 1300
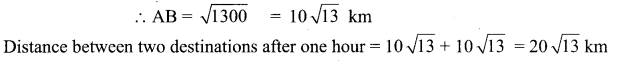
Question 16.
Suppose that a satellite in space, an earth station, and the centre of earth all lie in the same plane. Let r be the radius of earth and R be the distance from the centre of the earth to the satellite. Let d be the distance from the earth station to the satellite. Let 30° be the angle of elevation from the earth station to the satellite. If the line segment connecting earth station and satellite subtends angle α at the centre of the earth, then prove that
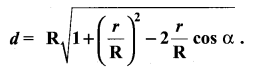
Solution:
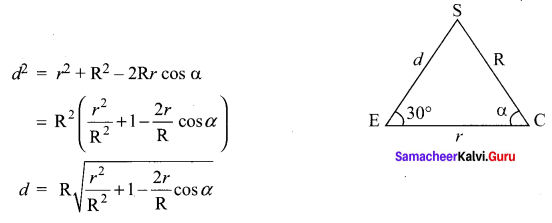
Samacheer Kalvi 11th Maths Solutions Chapter 3 Trigonometry Ex 3.10 Additional Questions Solved
Question 1.
Given a = 8, b = 9, c = 10, find all the angles.
Solution:

![]()
Question 2.
Given a = 31, b = 42, c = 57, find all the angles.
Solution:
Since the sides are larger quantities, use half angles formulae
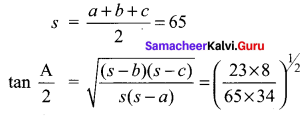
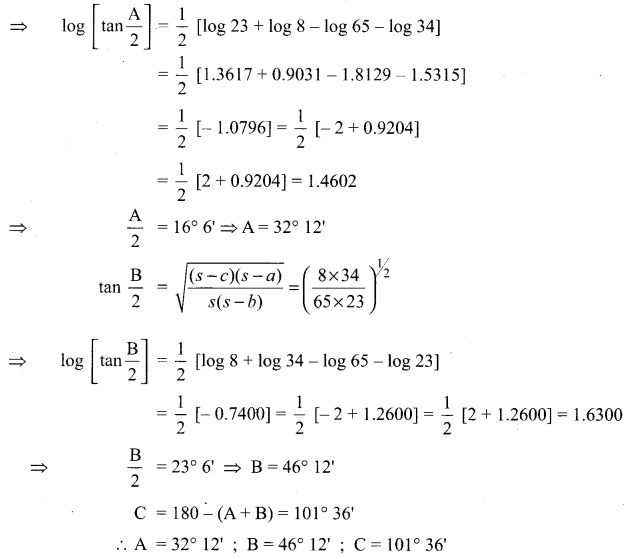
Question 3.
In a triangle ABC, A = 35° 17′ ; C = 45° 13′ ; b = 42.1 Solve the triangle
Solution:
The unknown parts are B, a, c,
B = 180 – (A + C) = 180 – (35° 17′ + 45° 13′)
= 99° 30′
To find sides, use sine formula
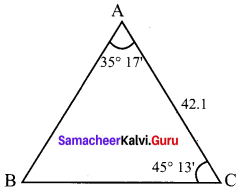

log c = log 42.1 + log sin 45° 31 – log sin 99° 30′
= 1.6243 + 1.8511 – 1.9940
= 1.4754 – 1.9940
= 1.4754 – [-1 + 0.9940] = 1.4814
⇒ c = 30.3°
Thus B = 99° 30′ ; a = 24.65° ; c = 30.3°
![]()
Question 4.
Solve the triangle ABC if a = 5, b = 4 and C = 68°.
Solution:
To find c, use c2 = a2 + b2 – 2ab cos C
c2 = 25 + 16 – 2 × 5 × 4 cos 68°
= 41 – 40 × 0.3746 = 26.016
c = 5.1
To find the other two angles, use sine formula.
