You can Download Samacheer Kalvi 12th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 1 Applications of Matrices and Determinants Ex 1.5
Question 1.
Solve the following systems of linear equations by Gaussian elimination method:
(i) 2x – 2y + 3z = 2, x + 2y – z = 3, 3x – y + 2z = 1
(ii) 2x + 4y + 6z = 22, 3x + 8y + 5z = 27, -x + y + 2z = 2
Solution:
(i) 2x – 2y + 3z = 2, x + 2y – z = 3 and 3x – y + 2z = 1
The matrix form of the above equations is \(\left(\begin{array}{rrr}{2} & {-2} & {3} \\ {1} & {2} & {-1} \\ {3} & {-1} & {2}\end{array}\right)\left(\begin{array}{l}{x} \\ {y} \\ {z}\end{array}\right)=\left(\begin{array}{l}{2} \\ {3} \\ {1}\end{array}\right)\)
(i.e) AX = B
The augment matrix (A, B) is

The above matrix is in echelon form.
Now writing the equivalent equations
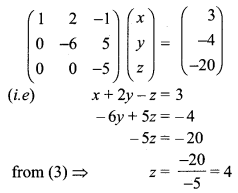
Substituting z = 4 in (2) we get
-6y + 20 = -4
⇒ -6y = -4 – 20 = -24
⇒ y = 4
Substituting z = 4 and y = 4 in (1) we get
x + 8 – 4 = 3
⇒ x + 4 = 3
⇒ x = 3 – 4 = -1
So, x = -1; y = 4; z = 4
(ii) 2x + 4y + 6z = 22 …… (1)
3x + 8y + 5z = 27 ……. (2)
-x + y + 2z = 2 ……. (3)
Divide equation (1) by 2 we get
x + 2y + 3z = 11 ……. (1)
3x + 8y + 5z = 27 …….. (2)
-x + y + 2z = 2 ……. (3)
The matrix form of the above equations is \(\left(\begin{array}{ccc}{1} & {2} & {3} \\ {3} & {8} & {5} \\ {-1} & {1} & {2}\end{array}\right)\left(\begin{array}{l}{x} \\ {y} \\ {z}\end{array}\right)=\left(\begin{array}{c}{11} \\ {27} \\ {2}\end{array}\right)\)
(i.e) AX = B
The augment matrix (A, B) is
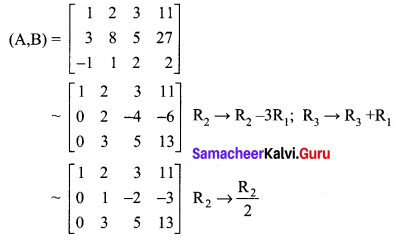
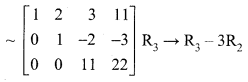
The above matrix is in echelon form.
Now writing the equivalent equations.
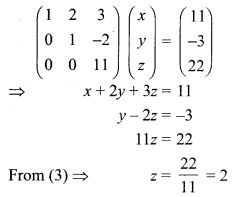
Substituting z = 2 in (2) we get
y – 4 = -3
⇒ y = -3 + 4 = 1
Substituting z = 2, y = 1 in (1) we get
x + 2(1) + 3(2) = 11
⇒ x + 2 + 6 = 11
⇒ x + 8 = 11
⇒ x = 11 – 8 = 3
x = 3, y = 1, z = 2
![]()
Question 2.
If ax2 + bx + c is divided by x + 3, x – 5, and x – 1, the remainders are 21, 61 and 9 respectively. Find a, b and c. (Use Gaussian elimination method.)
Solution:
P(x) = ax2 + bx + c. When P(x) is divided by x + 3, x – 5 and x – 1.
The remainders are respectively P(-3), P (5), and P (1).
We are given that P(-3) = 21; P(5) = 61; P(1) = 9
Now P(-3) = 21
⇒ a(-3)2 + b(-3) + c = 21
⇒ 9a – 3b + c = 21 ……. (1)
P(5) = 61
⇒ a(5)2 + b(5) + c = 61
⇒ 25a + 5b + c = 61 ……. (2)
P(1) = 9
⇒ a(1)2 + b(1) + c = 9
⇒ a + b + c = 9 …… (3)
Now the matrix form of the above three equations is \(\left(\begin{array}{ccc}{9} & {-3} & {1} \\ {25} & {5} & {1} \\ {1} & {1} & {1}\end{array}\right)\left(\begin{array}{l}{a} \\ {b} \\ {c}\end{array}\right)=\left(\begin{array}{c}{21} \\ {61} \\ {9}\end{array}\right)\)
(i.e) AX = B
The augmented matrix (A, B) is

The above matrix is in echelon form now writing the equivalent equations.
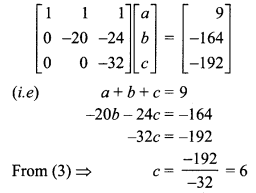
Substituting c = 6 in (2) we get
-20b – 24(6) = -164
⇒ -20b = -164 + 144 = -20
⇒ b = 1
Substituting c = 6, b = 1 in (1) we get
a + 1 + 6 = 9
⇒ a = 9 – 7 = 2
So a = 2, b = 1, c = 6
Question 3.
An amount of ₹ 65,000 is invested in three bonds at the rates of 6%, 8% and 10% per annum respectively. The total annual income is ₹ 5,000. The income from the third bond is ₹ 800 more than that from the second bond. Determine the price of each bond. (Use Gaussian elimination method.)
Solution:
Let the amount invested in 6% bond be ₹ x
and the amount invested in 8% bond be ₹ y
and the amount invested in 10% bond be ₹ z
Now x + y + z = 65000 ……. (1)
\(\frac{6}{100} x+\frac{8}{100} y+\frac{10}{100} z=5000\)
(i.e) 6x + 8y + 10z = 500000
(÷ by 2) 3x + 4y + 5z = 250000 ……. (2)
Also given that \(\frac{10}{100} z-\frac{8}{100} y=800\)
(i.e) -8y + 10z = 80000
(÷ by 2) -4y + 5z = 40000 …… (3)
Now the matrix form of the above three equations is \(\left(\begin{array}{ccc}{1} & {1} & {1} \\ {3} & {4} & {5} \\ {0} & {-4} & {5}\end{array}\right)\left(\begin{array}{l}{x} \\ {y} \\ {z}\end{array}\right)=\left(\begin{array}{c}{65000} \\ {250000} \\ {40000}\end{array}\right)\)
(i.e) AX = B
Now, the augmented matrix (A, B) is

Now the above matrix is in echelon form. Writing the equivalent equations.
\(\left(\begin{array}{lll}{1} & {1} & {1} \\ {0} & {1} & {2} \\ {0} & {0} & {13}\end{array}\right)\left(\begin{array}{l}{x} \\ {y} \\ {z}\end{array}\right)=\left(\begin{array}{r}{65000} \\ {55000} \\ {260000}\end{array}\right)\)
(i.e) x + y + z = 65000
⇒ y + 2z = 55000
⇒ 13z = 260000
⇒ z = ₹ 20000
Substituting z = ₹ 20000 in (2) we get
y + 40000 = 55000
⇒ y = 55000 – 40000 = ₹ 15000
Substituting z = ₹ 20000, y = ₹ 15000 in (1) we get
x + 15000 + 20000 = 65000
⇒ x = 65000 – 35000 = ₹ 30000
So the amount invested in
6% bond x = ₹ 30000
8% bond y = ₹ 15000
and 10% bond z = ₹ 20000
![]()
Question 4.
A boy is walking along the path y = ax2 + bx + c through the points (-6, 8), (-2, -12), and (3, 8). He wants to meet his friend at P(7, 60). Will he meet his friend? (Use Gaussian elimination method.)
Solution:
We are given y = ax2 + bx + c
Also we are given (-6, 8), (-2, -12) and (3, 8) are points on the path.
(i) (-6, 8) is a point on y = ax2 + bx + c
at x = -6, y = 8
(i.e) a(36) + b(-6) + c = 8
⇒ 36a – 6b + c = 8 …… (1)
(ii) (-2, -12) is a point on y = ax2 + bx + c
at x = -2, y = -12
⇒ a(-2)2 + b(-2) + c = -12
⇒ 4a – 2b + c = -12 ….. (2)
(iii) (3, 8) is a point on y = ax2 + bx + c
at x = 3, y = 8
⇒ a(3)2 + 6(3) + c = 8
⇒ 9a + 3b + c = 8 …… (3)
The matrix form of the above three equations is \(\left(\begin{array}{ccc}{36} & {-6} & {1} \\ {4} & {-2} & {1} \\ {9} & {3} & {1}\end{array}\right)\left(\begin{array}{l}{a} \\ {b} \\ {c}\end{array}\right)=\left(\begin{array}{c}{8} \\ {-12} \\ {8}\end{array}\right)\)
(i.e) AX = B
The augmented matrix (A, B) is

The above matrix is in echelon form. Now writing the equivalent equations we get
\(\left(\begin{array}{ccc}{36} & {-6} & {1} \\ {0} & {-12} & {8} \\ {0} & {0} & {30}\end{array}\right)\left(\begin{array}{l}{a} \\ {b} \\ {c}\end{array}\right)=\left(\begin{array}{c}{8} \\ {-116} \\ {-300}\end{array}\right)\)
(i.e) 36a – 6b + c = 8
⇒ -12b + 8c = -116
⇒ 30c = -300
⇒ c = -10
Substituting c = -10 in (2) we get
-12b + 8(-10) = -116
⇒ -12b = -116 + 80 = -36
⇒ b = 3
Substituting c = -10, b = 3 in (1) we get
36a – 6(3) + (-10) = 8
⇒ 36a – 18 – 10 = 8
⇒ 36a = 8 + 18 + 10 = 36
⇒ a = 1
a = 1, b = 3 and c = -10
y = (1)x2 + (3)x + (-10)
y = x2 + 3x – 10
Now at x = 7, y= (7)2 + 3(7)- 10 = 49 + 21 – 10 = 60
(7, 60) is a point on the path so he will meet his friend.
![]()
Samacheer Kalvi 12th Maths Solutions Chapter 1 Applications of Matrices and Determinants Ex 1.5 Additional Problems
Question 1.
Examine the consistency of the following system of equations. If it is consistent then solve the same.
(i) 4x + 3y + 6z = 25,
x + 5y + 7z = 13,
2x + 9y + z = 1
Solution:
The augmented matrix is
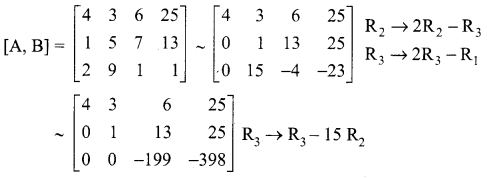
The last equivalent matrix is in the echelon form. It has three non-zero rows.
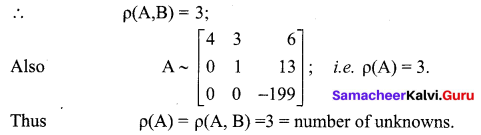
∴ The given system is consistent and has a unique solution
4x + 3y + 6z = 25 …… (1)
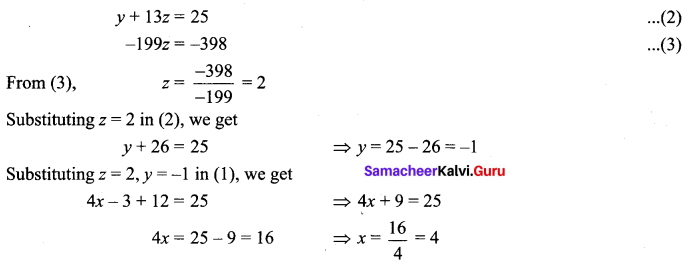
∴ The unique solution is x = 4, y = -1, z = 2.
Question 2.
Verify whether the given system of equations is consistent. If it is consistent, solve them. 2x + 5y + 7z = 52, x + 7 + z = 9, 2x + y – z = 0
Solution:
The given system of equations is equivalent to the single matrix equation.
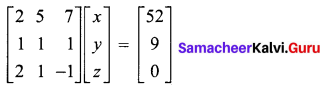
AX = B
The augmented matrix is

The last equivalent matrix is in the echelon form. It has three non-zero rows.
∴ \(\rho(\mathrm{A}, \mathrm{B})=3\)
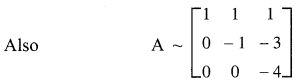
Since there are three non-zero rows, \(\rho(\mathrm{A})\) = 3
![]()
The given system is consistent and has a unique solution.
To find the solution, we see that the given system of equations is equivalent to the matrix equation.
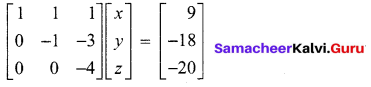
x + y + z = 9 ……. (1)
-y – 3z = -18 ……… (2)
-4z = -20 ……… (3)
(3) ⇒ z = 5, (2) ⇒ y = 18 – 3z = 13, (1) ⇒ x = 9 – y – z ⇒ x = 9 – 3 – 5 = 1
∴ Solution is x = 1,
y = 3,
z = 5
![]()
Question 3.
Examine the consistency of the equations.
2x – 3y + 3z = 5,
3x + y – 3z = 13,
2x + 19y – 47z = 32
Solution:
The given system of equations can be written in the form of a matrix equation as
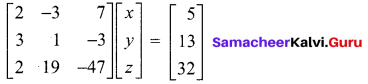
The augmented matrix is
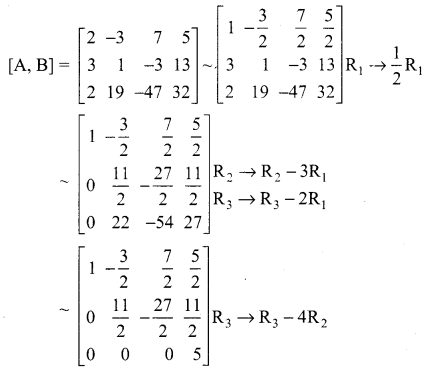
The last equivalent matrix is in the echelon form. It has three non-zero rows.
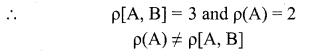
∴ The given system is inconsistent and hence has no solution.
Question 4.
Show that the equations: x + y + z = 6, x + 2y + 3z = 14, x + 4y + 7z = 30 are consistent and solve them.
Solution:
The matrix equation corresponding to the given system is.
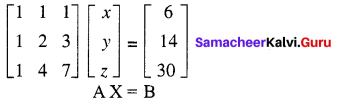
The augmented matrix is
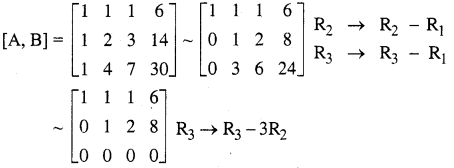
In the last equivalent matrix, there are two non-zero rows.
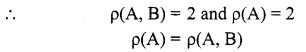
∴ The given system is consistent. But the value of the common rank is less than the number of unknowns. The given system has an infinite number of solutions.
The given system is equivalent to the matrix equation
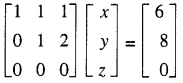
x + y + z = 6 ……(1)
y + 2z = 8 ….(2)
(2) ⇒ y = 8 – 2z ; (1) ⇒ x = 6 – y – z = 6 – (8 – 2z) – z = z – 2
Taking z = k, we get x = k – 2, y = 8 – 2k; k ∈ R
Putting k = 1, we have one solution as x = – 1, y = 6, z = 1. Thus by giving different values for k we get different solutions. Hence the given system has infinite number of solutions.