Students can download 12th Business Maths Chapter 8 Sampling Techniques and Statistical Inference Ex 8.1 Questions and Answers, Samacheer Kalvi 12th Business Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 12th Business Maths Solutions Chapter 8 Sampling Techniques and Statistical Inference Ex 8.1
Question 1.
What is the population?
Solution:
A population is a set of similar items or events which is of interest for some question or experiment. A population can be specific or vague. Examples of population defined vaguely include the number of newborn babies in Tamil Nadu, a total number of tech startups in India, the average height of all exam candidates, mean weight of taxpayers in Chennai etc. Examples of population defined specifically include a number of fans produced in a particular factory, the number of students in a class, the number of boys and girls in a tuition centre etc.
Question 2.
What is the sample?
Solution:
A sample is a set of data collected from a statistical population by a defined procedure. The elements of a sample are called sample size or sample points. Samples are collected and statistics are calculated from the samples, so that one can make inferences from the sample to the population.
![]()
Question 3.
What is statistic?
Solution:
A statistic is used to estimate the value of a population parameter. For instance, we selected a random sample of 100 students from a school with 1000 students. The average height of the sampled students would be an example of a statistic. Examples, sample variance, sample quartiles, sample percentiles, sample moments etc.
Question 4.
Define parameter.
Solution:
A parameter is any numerical quantity that characterizes a given population or some aspect of it. This means the parameter tells us something about the whole population. For example, the population mean µ, variance σ2, population proportion P, population correlation ρ.
![]()
Question 5.
What is the sampling distribution of a statistic?
Solution:
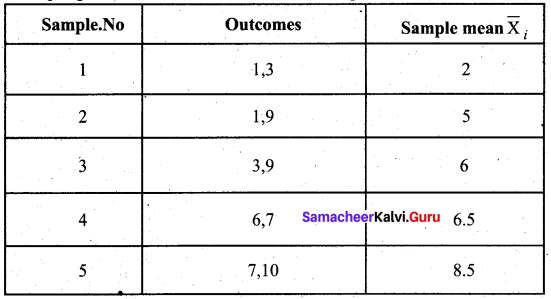
Sampling distribution of a statistic is the probability distribution of a given random sample based statistic. It may be considered as the distribution of the statistic for all possible samples from the same population of a given sample size.
Example, the sampling distribution of the mean for n = 2 is given below:
Question 6.
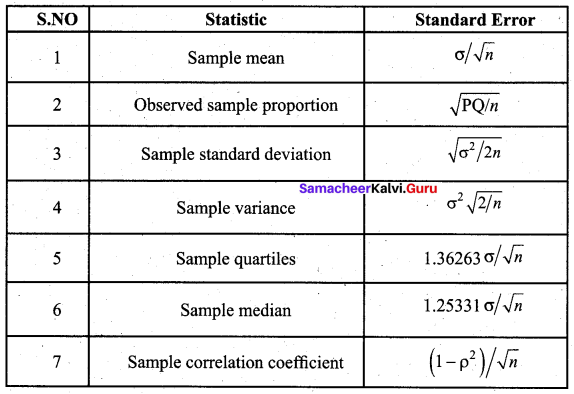
What is the standard error?
Solution:
The standard error (S.E) of a statistic is the standard deviation of its sampling distribution. If the parameter or the statistic is the mean, it is called the standard error of the mean (SEM). The standard error provides a rough estimate of the interval in which the population parameters is likely to fall.
![]()
Question 7.
Explain in detail about simple random sampling with a suitable example.
Solution:
(i) Simple random sampling:
In this technique, the samples are selected in such a way that each and every unit in the population has an equal and independent chance of being selected as a sample. Simple random sampling may be done, with or without replacement of the samples selected. In a simple random sampling with replacement, there is a possibility of selecting the same sample any number of times. So, simple random sampling without replacement is followed.
Thus in simple random sampling from a population of N units, the probability of drawing any unit at the first draw is \(\frac{1}{N}\), the probability of drawing any unit in the second draw from among the available (N – 1) units is \(\frac{1}{(N-1)}\), and so on. Several methods have been adopted for random selection of the samples from the population. Of those, the following two methods are generally used and which are described below.
1. Lottery method
This is the most popular and simplest method when the population is finite. In this method, all the items of the population are numbered on separate slips of paper of the same size, shape and colour. They are folded and placed in a container and shuffled thoroughly. Then the required numbers of slips are selected for the desired sample size. The selection of items thus depends on chance.
For example, if we want to select 10 students, out of 100 students, then we must write the names/roll number of all the 100 students on slips of the same size and mix them, then we make a blindfold selection of 10 students. This method is called unrestricted random sampling because units are selected from the population without any restriction. This method is mostly used in lottery draws. If the population or universe is infinite, this method is inapplicable.
2. Table of Random number
When the population size is large, it is difficult to number all the items on separate slips of paper of same size, shape and colour. The alternative method is that of using the table of random numbers. The most practical, easy and inexpensive method of selecting a random sample can be done through “Random Number Table”. The random number table has been so constructed that each of the digits 0, 1, 2,…, 9 will appear approximately with the same frequency and independently of each other.
The various random number tables available are
- L.H.C. Tippett random number series
- Fisher and Yates random number series
- Kendall and Smith random number series
- Rand Corporation random number series.
Tippett’s table of random numbers is most popularly used in practice.
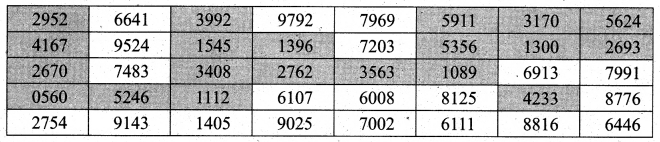
An example to illustrate how Tippett’s table of random numbers may be used is given below. Suppose we have to select 20 items out of 6,000. The procedure is to number all the 6,000 items from 1 to 6,000. A page from Tippett’s table may be selected and the first twenty numbers ranging from 1 to 6,000 are noted down. If the numbers are above 6000, choose the next number ranging from 1 to 6000. Items bearing those numbers will be selected as samples from the population. Making use of the portion of the random number table given, the required random samples are shaded. Here, we consider row-wise selection of random numbers.
Question 8.
Explain the stratified random sampling with a suitable example.
Solution:
Stratified Random Sampling
In stratified random sampling, first divide the population into subpopulations, which are called strata. Then, the samples are selected from each of the strata through random techniques. The collection of all the samples from all strata gives the stratified random samples.
When the population is heterogeneous or different segments or groups with respect to the variable or characteristic under study, then the Stratified Random Sampling method is studied.. First, the population is divided into the homogeneous number of sub-groups or strata before the sample is drawn. A sample is drawn from each stratum at random. Following steps are involved in selecting a random sample in a stratified random sampling method.
![]()
(a) The population is divided into different classes so that each stratum will consist of more or less homogeneous elements. The strata are so designed that they do not overlap each other.
(b) After the population is stratified, a sample of a specified size is drawn at random from each stratum using Lottery Method or Table of Random Number Method.
Stratified random sampling is applied in the field of the different legislative areas as strata in election polling, division of districts (strata) in a state etc…
Ex: From the following data, select 68 random samples from the population of the heterogeneous group with a size of 500 through stratified random sampling, considering the following categories as strata.
- Category 1: Lower income class – 39%
- Category 2: Middle income class – 38%
- Category 3: Upper income class – 23%
Solution:
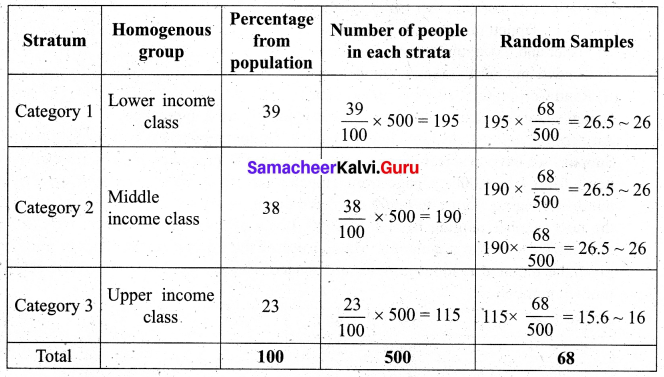
Question 9.
Explain in detail about systematic random sampling with example.
Solution:
Systematic sampling:
In systematic sampling, randomly select the first sample from the first k units. Then every kth member, starting with the first selected sample, is included in the sample.
Systematic sampling is a commonly used technique if the complete and up-to-date list of the sampling units is available. We can arrange the items in numerical, alphabetical, geographical or in any other order. The procedure of selecting the samples starts with selecting the first sample at random, the rest being automatically selected according to some pre-determined ( pattern. A systematic sample is formed by selecting every item from the population, where k refers to the sample interval. The sampling interval can be determined by dividing the size of the population by the size of the sample to be chosen.
That is k = \(\frac{\mathrm{N}}{n}\), where k is an integer.
k = Sampling interval, N = Size of the population, n = Sample size.
Procedure for selection of samples by systematic sampling method
(i) If we want to select a sample of 10 students from a class of 100 students, the sampling interval is calculated as \(k=\frac{N}{n}=\frac{100}{10}=10\)
Thus sampling interval = 10 denotes that for every 10 samples one sample has to be selected.
(ii) The first sample is selected from the first 10 (sampling interval) samples through random selection procedures.
(iii) If the selected first random sample is 5, then the rest of the samples are automatically selected by incrementing the value of the sampling interval (k = 10) i.e., 5, 15, 25, 35, 45, 55, 65, 75, 85, 95.
![]()
Ex: Suppose we have to select 20 items out of 6,000. The procedure is to number all the 6,000 items from 1 to 6,000. The sampling interval is calculated as k = \(\frac{N}{n}=\frac{6000}{20}\) = 300. Thus sampling interval = 300 denotes that for every 300 samples one sample has to be selected. The first sample is selected from the first 300 (sampling interval) samples through random selection procedures. If the selected first random sample is 50, then the rest of the samples are automatically selected by incrementing the value of the sampling interval (k = 300) ie,50, 350, 650, 950, 1250, 1550, 1850, 2150, 2450, 2750, 3050, 3350, 3650, 3950, 4250, 4550, 4850, 5150, 5450, 5750. Items bearing those numbers will be selected as samples from the population.
Question 10.
Explain in detail about sampling error.
Solution:
Sampling Errors: Errors, which arise in the normal course of investigation or enumeration on account of chance, are called sampling errors. Sampling errors are inherent in the method of sampling. They may arise accidentally without any bias or prejudice.
Sampling Errors arise primarily due to the following reasons:
- Faulty selection of the sample instead of the correct sample by defective sampling technique.
- The investigator substitutes a convenient sample if the original sample is not available while investigation.
- In area surveys, while dealing with borderlines it depends upon the investigator whether to include them in the sample or not. This is known as Faulty demarcation of sampling units.
Question 11.
Explain in detail about the non-sampling error.
Solution:
Non-Sampling Errors:
The errors that arise due to human factors which always vary from one investigator to another in selecting, estimating or using measuring instruments( tape, scale) are called Non-Sampling errors.
It may arise in the following ways:
- Due to negligence and carelessness of the part of either investigator or respondents.
- Due to the lack of trained and qualified investigators.
- Due to the framing of a wrong questionnaire.
- Due to applying the wrong statistical measure
- Due to incomplete investigation and sample survey.
Question 12.
State any two merits of simple random sampling.
Solution:
- In simple random sampling personal bias is completely eliminated.
- This method is economical as it saves time, money and labour.
Question 13.
State any three merits of stratified random sampling.
Solution:
- A random stratified sample is superior to a simple random sample because it ensures representation of all groups and thus it is more representative of the population which is being sampled.
- A stratified random sample can be kept small in size without losing its accuracy.
- It is easy to administer if the population under study is sub-divided.
![]()
Question 14.
State any two demerits of systematic random sampling.
Solution:
- Systematic samples are not random samples.
- If N is not a multiple of n, then the sampling interval (k) cannot be an integer, thus sample selection becomes difficult.
Question 15.
State any two merits for systematic random sampling.
Solution:
Merits of systematic sampling are given below:
- This method distributes the sample more evenly over the entire listed population.
- The time and work are reduced much.
Question 16.
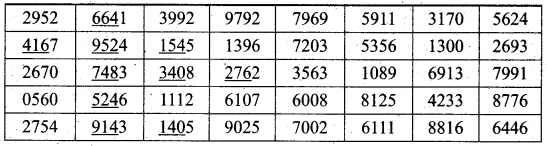
Using the following Tippet’s random number table.
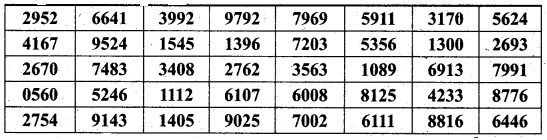
Draw a sample of 10 three-digit numbers which are even numbers.
Solution:
There are many ways to select a sample of 10 3-digit even numbers. From the table, start from the first number and move along the column. Select the first three digits as the number. If it is an odd number, move to the next number. The selected sample is 416, 664, 952, 748, 524, 914, 154, 340, 140, 276.
Question 17.
A wholesaler in apples claims that only 4 % of the apples supplied by him are defective. A random sample of 600 apples contained 36 defective apples. Calculate the standard error concerning good apples.
Solution:
Sample size = 600
No. of defective apples = 36
Sample proportion p = \(\frac{36}{600}\) = 0.06
Population proportion P = probability of defective apples = 4% = 0.04
Q = 1 – P = 1 – 0.04 = 0.96
The S.E for sample proportion is given by S.E
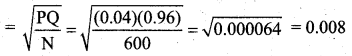
![]()
Question 18.
A sample of 1000 students whose mean weight is 119 lbs (pounds) from a school in Tamil Nadu State was taken and their average weight was found to be 120 lbs with a standard deviation of 30 lbs. Calculate the standard error of the mean.
Solution:
Given n = 1000, \(\bar{X}\) = 119, σ = 30
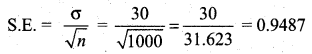
Question 19.
A random sample of 60 observations was drawn from a large population and its standard deviation was found to be 2.5. Calculate the suitable standard error that this sample is taken from a population with standard deviation 3?
Solution:
Given sample size n = 60
Sample standard deviation = 2.5
Population standard deviation σ = 3
The S.E is given by
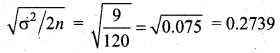
![]()
Question 20.
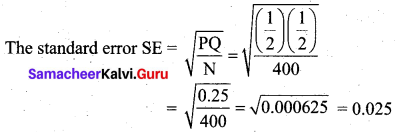
In a sample of 400 population from a village 230 are found to be eaters of vegetarian items and the rest non-vegetarian items. Compute the standard error assuming that both vegetarian and non-vegetarian foods are equally popular in that village?
Solution:
Given sample size 400 and 230 are vegetarian eaters.
So sample proportionp = \(\frac{230}{400}\) = 0.575
Population proportion P = Prob (vegetarian eaters from the village) = \(\frac{1}{2}\)
(Since vegetarian and non-vegetarian foods are equally popular)
Q = 1 – P = 1 – \(\frac{1}{2}\) = \(\frac{1}{2}\)