Samacheer Kalvi 12th Business Maths Solutions Chapter 6 Random Variable and Mathematical Expectation Ex 6.2

Students can download 12th Business Maths Chapter 6 Random Variable and Mathematical Expectation Ex 6.2 Questions and Answers, Samacheer Kalvi 12th Business Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 12th Business Maths Solutions Chapter 6 Random Variable and Mathematical Expectation Ex 6.2

Question 1.
Find the expected value for the random variable of an unbiased die.
Solution:
Let X denote the number on the top side of the unbiased die.
The probability mass function is given by the following table.

The expected value for the random variable X is E(X) = \(\sum_{x} x P_{x}(x)\)

Question 2.
Let X be a random variable defining number of students getting A grade. Find the expected value of X from the given table.

Solution:
Expected value of X, E(X) = \(\sum_{x} x P_{x}(x)\)
E(X) = (0 × 0.2) + (1 × 0.1) + (2 × 0.4) + (3 × 0.3)
= 0 + 0. 1 + 0.8 + 0.9
= 1.8

Question 3.
The following table is describing the probability mass function of the random variable X.

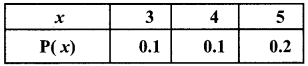
Find the standard deviation of x.
Solution:
The standard deviation of X, σ_x is given by σ_x = √Var[X]
Now Var(X) = E(X²) – [E(X)]²
From the given table,

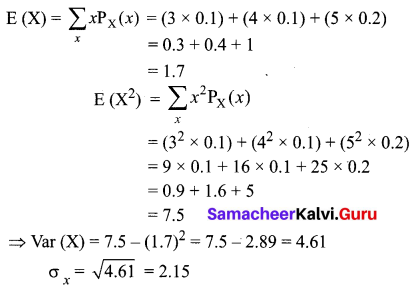
Hence the standard deviation of X is 2.15

Question 4.
Let X be a continuous random variable with probability density function.

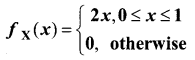
Find the expected value of X.
Solution:
The expected value of the random variable is given by E(X) = \(\int_{-\infty}^{\infty} x f(x) d x\)
According to the problem we have,

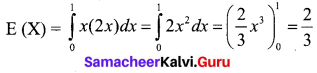
Question 5.
Let X be a continuous random variable with probability density function

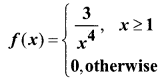
Find the mean and variance of X.
Solution:
Given that X is a continuous random variable.
The mean of X is the expected value of X.

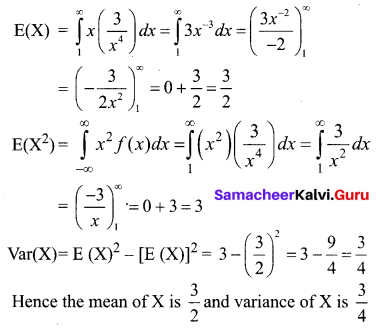
Question 6.
In investment, a man can make a profit of ₹ 5,000 with a probability of 0.62 or a loss of ₹ 8,000 with a probability of 0.38. Find the expected gain.
Solution:
Let X be the random variable which denotes the gain in the investment. It is given that X takes the value 5000 with probability 0.62 and -8000 with a probability 0.38.
(Note that we take -8000 since it is a loss)
The probability distribution is given by

E(X) = (0.38) (-8000) + (0.62) (5000)
= -3040 + 3100
= 60
Hence the expected gain is ₹ 60

Question 7.
What are the properties of Mathematical expectation?
Solution:
The properties of Mathematical expectation are as follows:
(i) E(a) = a, where ‘a’ is a constant
(ii) Addition theorem: For two r.v’s X and Y, E(X + Y) = E(X) + E(Y)
(iii) Multiplication theorem: E(XY) = E(X) E(Y)
(iv) E(aX) = aE(X), where ‘a’ is a constant
(v) For constants a and b, E(aX + b) = a E(X) + b

Question 8.
What do you understand by Mathematical expectation?
Solution:
The expected value of a random variable gives a measure of the center of the distribution of the variable. In other words, E(X) is the long-term average value of the variable. The expected value is calculated as a weighted average of the values of a random variable in a particular experiment. The weights are the probabilities. The mean of the random variable X is µ_X = E(X).

Question 9.
How do you define variance in terms of Mathematical expectation?
Solution:
Let X be a random variable. Let E(X) denote the expectation of X.
Then the variance is defined in terms of the mathematical expectation as follows.
(a) X is discrete r.v with p.m.f p(x). Then Var(X) = \(\sum[x-\mathrm{E}(\mathrm{X})]^{2} p(x)\)
(b) X is continuous r.v with p.d.f f_x(x). Then Var(X) = \(\int_{-\infty}^{\infty}[X-E(X)]^{2} f_{X}(x) d x\)

Question 10.
Define Mathematical expectation in terms of a discrete random variable.
Solution:
Let X be a discrete random variable with probability mass function (p.m.f) P(x). Then, its expected value is defined by E(X) = \(\sum_{x} x p(x)\)
In other words, if x₁, x₂, x₃,…… x_n are the different values of X, and p(x₁), p(x₂) …..p(x_n) are the corresponding probabilities, then E(X) = x₁ p(x₁) + x₂ p(x₂) + x₃ p(x₃) +… x_n p(x_n)

Question 11.
State the definition of Mathematical expectation using a continuous random variable.
Solution:
Let X be a continuous random variable with probability density function f(x). Then the expected value of X is
\(\mathrm{E}(\mathrm{X})=\int_{-\infty}^{\infty} x f(x) d x\)
If the integral exists, E(X) is the mean of the values, otherwise, we say that the mean does not exist.

Question 12.
In a business venture, a man can make a profit of ₹ 2,000 with a probability of 0.4 or have a loss of ₹ 1,000 with a probability of 0.6. What are his expected, variance and standard deviation of profit?
Solution:
Let X be the random variable denoting the profit of the business venture.
The probability distribution of X is given as follows

E(X) = (-1000) (0.6) + (2000) (0.4)
= – 600 + 800
= 200
E(X²) = (-1000)² (0.6) + (2000)² (0.4)
= 6,00,000 + 16,00,000
= 22,00,000
V(X) = E(X²) – [E(X)]²
= 22,00,000 – 40000
= 21,60,000
Standard deviation = √Var[X]
= \(\sqrt{2160000}\)
= 1469.69
Thus the expected value of profit is ₹ 200. The variance of profit is ₹ 21,60,000 and the standard deviation of profit is ₹ 1469.69.

Question 13.
The number of miles an automobile tyre lasts before it reaches a critical point in tread wear can be represented by a p.d.f.

Find the expected number of miles (in thousands) a tyre would last until it reaches the critical tread wear point.
Solution:
Let the continuous random variable X denote the number of miles (in thousands) till an automobile tyre lasts.
The expected value is E(X) = \(\int_{-\infty}^{\infty} x f(x) d x\)
From the problem we have,
\(E(X)=\int_{0}^{\infty}(x) \frac{1}{30} e^{\frac{-x}{30}} d x\)
We use integration by parts to evaluate the integral

Hence the expected number of miles is 30,000.

Question 14.
A person tosses a coin and is to receive ₹ 4 for a head and is to pay ₹ 2 for a tail. Find the expectation and variance of his gains.
Solution:
Let X be the discrete random variable which denotes the gain of the person.
The probability distribution of X is given by

(Here, since a coin is tossed the probability is equal for the outcomes head or tail)

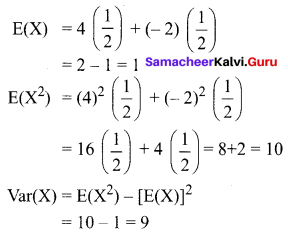
Thus the expectation of his gains is 1 and the variance of his gains is 9.

Question 15.
Let X be a random variable and Y = 2X + 1. What is the variance of Y if the variance of X is 5?
Solution:
Given X is a random variable and Y = 2X + 1 and Var(X ) = 5
Var (Y) = Var (2X + 1) = (2)² = 4
Var X = 4(5) = 20