Students can download 12th Business Maths Chapter 3 Integral Calculus II Ex 3.4 Questions and Answers, Samacheer Kalvi 12th Business Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 12th Business Maths Solutions Chapter 3 Integral Calculus II Ex 3.4
Choose the correct answer form the given alternatives.
Question 1.
Area bounded by the curve y = x(4 – x) between the limits 0 and 4 with x-axis is ________
(a) \(\frac{30}{3}\) sq.units
(b) \(\frac{31}{2}\) sq.units
(c) \(\frac{32}{3}\) sq.units
(d) \(\frac{15}{2}\) sq.units
Answer:
(c) \(\frac{32}{3}\) sq.units
Hint:
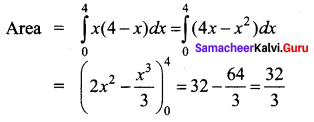
Question 2.
Area bounded by the curve y = e-2x between the limits 0 ≤ x ≤ ∞ is ______
(a) 1 sq.units
(b) \(\frac{1}{2}\) sq.unit
(c) 5 sq.units
(d) 2 sq.units
Answer:
(b) \(\frac{1}{2}\) sq.unit
Hint:

Question 3.
Area bounded by the curve y = \(\frac{1}{x}\) between the limits 1 and 2 is ________
(a) log 2 sq.units
(b) log 5 sq.units
(c) log 3 sq.units
(d) log 4 sq.units
Answer:
(a) log 2 sq.units
Hint:
Area A = \(\int _{1}^{2}\) ydx = \(\int _{1}^{2}\) \(\frac { 1 }{x}\) dx = [log x]\(_{1}^{2}\)
= log 2 – log 1 = log (2/1) = log (2)
Question 4.
If the marginal revenue function of a firm is MR = \(e^{\frac{-x}{10}}\), then revenue is ______
(a) \(-10 e^{\frac{-x}{10}}\)
(b) \(1-e^{\frac{-x}{10}}\)
(c) \(10\left(1-e^{\frac{-x}{10}}\right)\)
(d) \(e^{\frac{-x}{10}}+10\)
Answer:
(c) \(10\left(1-e^{\frac{-x}{10}}\right)\)
Hint:

Question 5.
If MR and MC denotes the marginal revenue and marginal cost functions, then the profit functions is ________
(a) P = ∫(MR – MC) dx + k
(b) P = ∫(MR + MC) dx + k
(c) P = ∫(MR) (MC) dx + k
(d) P = ∫(R – C) dx + k
Answer:
(a) P = ∫(MR – MC) dx + k
Hint:
Profit = Revenue – Cost
Question 6.
The demand and supply functions are given by D(x) = 16 – x2 and S(x) = 2x2 + 4 are under perfect competition, then the equilibrium price x is ________
(a) 2
(b) 3
(c)4
(d) 5
Answer:
(a) 2
Hint:
D(x) = 16 – x2 , S(x) = 2x2 + 4
Under equilibriuim, D(x) = S(x)
⇒ 16 – x2 = 2x2 + 4
⇒ 3x2 = 12
⇒ x = ±2.
Since x cannot be negative x = 2.
Question 7.
The marginal revenue and marginal cost functions of a company are MR = 30 – 6x and MC = -24 + 3x where x is the product, then the profit function is _______
(a) 9x2 + 54x
(b) 9x2 – 54x
(c) 54x – \(\frac{9 x^{2}}{2}\)
(d) 54x – \(\frac{9 x^{2}}{2}\) + k
Answer:
(d) 54x – \(\frac{9 x^{2}}{2}\) + k
Hint:
Profit P = ∫(MR – MC) dx
= ∫[(30 – 6x) – (-24 + 3x)] dx
= ∫(30 – 6x + 24 – 3x) dx
= ∫(54 – 9x) dx = 54x – \(\frac { 9x^2 }{2}\) + k
Question 8.
The given demand and supply function are given by D(x) = 20 – 5x and S(x) = 4x + 8 if they are under perfect competition then the equilibrium demand is _______
(a) 40
(b) \(\frac{41}{2}\)
(c) \(\frac{40}{3}\)
(d) \(\frac{41}{5}\)
Answer:
(c) \(\frac{40}{3}\)
Hint:
D(x) = S(x) in equilibrium
20 – 5x = 4x + 8
9x = 12
x = \(\frac{4}{3}\) = x0
p0 = 20 – 5(\(\frac{4}{3}[/ltex])
= 20 – [latex]\frac{20}{3}\)
= \(\frac{40}{3}\)
Question 9.
If the marginal revenue MR = 35 + 7x – 3x2, then the average revenue AR is _______
(a) 35x + \(\frac{7 x^{2}}{2}\) – x3
(b) 35x + \(\frac{7 x}{2}\) – x2
(c) 35 + \(\frac{7 x}{2}\) + x2
(d) 35 + 7x + x2
Answer:
(b) 35x + \(\frac{7 x}{2}\) – x2
Hint:
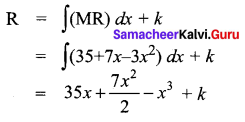

Question 10.
The profit of a function p(x) is maximum when _______
(a) MC – MR = 0
(b) MC = 0
(c) MR = 0
(d) MC + MR = 0
Answer:
(a) MC – MR = 0
Hint:
P = Revenue – Cost
P is maximum when \(\frac{d p}{d x}\) = 0
\(\frac{d p}{d x}\) = R'(x) – C'(x) = MR – MC = 0
Question 11.
For the demand function p(x), the elasticity of demand with respect to price is unity then ________
(a) revenue is constant
(b) cost function is constant
(c) profit is constant
(d) none of these
Answer:
(a) revenue is constant
Hint:

Question 12.
The demand function for the marginal function MR = 100 – 9x2 is _______
(a) 100 – 3x2
(b) 100x – 3x2
(c) 100x – 9x2
(d) 100 + 9x2
Answer:
(a) 100 – 3x2
Hint:
R = ∫MR dx = ∫(100 – 9x²) dx
R = 100x – \(\frac { 9x^3 }{3}\) + k
when x = 0, R = 0, then k = 0
∴ R = 100x – 3x³
Demand function
p = \(\frac { R }{x}\) = \(\frac { 100x – 3x^3 }{x}\) = 100 – 3x²
Question 13.
When x0 = 5 and p0 = 3 the consumer’s surplus for the demand function pd = 28 – x2 is _______
(a) 250 units
(b) \(\frac{250}{3}\) units
(c) \(\frac{251}{2}\) units
(d) \(\frac{251}{3}\) units
Answer:
(b) \(\frac{250}{3}\) units
Hint:
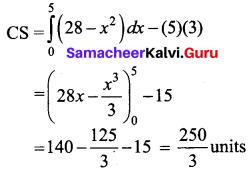
Question 14.
When x0 = 2 and P0 = 12 the producer’s surplus for the supply function Ps = 2x2 + 4 is _______
(a) \(\frac{31}{5}\) units
(b) \(\frac{31}{2}\) units
(c) \(\frac{32}{3}\) units
(d) \(\frac{30}{7}\) units
Answer:
(c) \(\frac{32}{3}\) units
Hint:

Question 15.
Area bounded by y = x between the lines y = 1, y = 2 with y-axis is ______
(a) \(\frac{1}{2}\) sq.units
(b) \(\frac{5}{2}\) sq.units
(c) \(\frac{3}{2}\) sq.units
(d) 1 sq.unit
Answer:
(c) \(\frac{3}{2}\) sq.units
Hint:
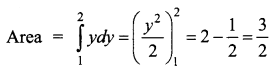
Question 16.
The producer’s surplus when the supply function for a commodity is P = 3 + x and x0 = 3 is _______
(a) \(\frac{5}{2}\)
(b) \(\frac{9}{2}\)
(c) \(\frac{3}{2}\)
(d) \(\frac{7}{2}\)
Ans:
(b) \(\frac{9}{2}\)
Hint:
x0 = 3, p = 3 + x ⇒ p0 = 3 + 3 = 6
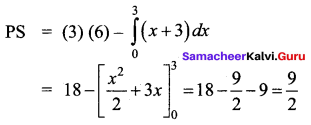
Question 17.
The marginal cost function is MC = 100√x. find AC given that TC = 0 when the output is zero is ______
(a) \(\frac{200}{3} x^{\frac{1}{2}}\)
(b) \(\frac{200}{3} x^{\frac{3}{2}}\)
(c) \(\frac{200}{3 x^{\frac{3}{2}}}\)
(d) \(\frac{200}{3 x^{\frac{1}{2}}}\)
Answer:
(a) \(\frac{200}{3} x^{\frac{1}{2}}\)
Hint:

Question 18.
The demand and supply function of a commodity are P(x) = (x – 5)2 and S(x) = x2 + x + 3 then the equilibrium quantity x0 is ________
(a) 5
(b) 2
(c) 3
(d) 19
Answer:
(b) 2
Hint:
P(x) = S(x)
(x – 5)² = x² + x + 3
x² – 10x + 25 = x² + x + 3
⇒ 25 – 3 = x + 10x
⇒ 11x = 22
⇒ x = 2
Question 19.
The demand and supply function of a commodity are D(x) = 25 – 2x and S(x) = \(\frac{10+x}{4}\) then the equilibrium price p0 is _________
(a) 5
(b) 2
(c) 3
(d) 10
Answer:
(a) 5
Hint:
At market equilibrium, D(x) = S(x)
25x – 2x = \(\frac { 10+x }{4}\) ⇒ 4(25 – 2x) = 10 + x
100 – 8x = 10 + x ⇒ 100 – 10 = x + 8x
9x = 90 ⇒ x = 10
when x = 10 P = 25 – 2 (10) = 25 – 20 = 5
Question 20.
If MR and MC denote the marginal revenue and marginal cost and MR – MC = 36x – 3x2 – 81, then the maximum profit at x is equal to _______
(a) 3
(b) 6
(c) 9
(d) 5
Answer:
(c) 9
Hint:
The maximum profit occurs when MR – MC = 0
⇒ 36x – 3x2 – 81 = 0
⇒ x2 – 12x + 27 = 0
⇒ (x – 9)(x – 3) = 0
⇒ x = 9, 3
Now \(\frac{d p}{d x}\) = 36x – 3x2 – 81 ⇒ \(\frac{d^{2} p}{d x^{2}}\) = 36 – 9x
At x = 9, \(\frac{d^{2} p}{d x^{2}}\) = 36 – 81 < 0
At x = 3, \(\frac{d^{2} p}{d x^{2}}\) = 36 – 27 > 0
Therefore profit is maximum when x = 9.
Question 21.
If the marginal revenue of a firm is constant, then the demand function is ________
(a) MR
(b) MC
(c) C(x)
(d) AC
Answer:
(a) MR
Hint:
MR = k (constant)
Revenue function R = ∫(MR) dx + c1
= ∫kdx + c1
= kx + c1
When R = 0, x = 0, ⇒ c1 = 0
R = kx
Demand function p = \(\frac{R}{x}=\frac{k x}{x}\) = k constant
⇒ p = MR
Question 22.
For a demand function p, if \(\int \frac{d p}{p}=k \int \frac{d x}{x}\) then k is equal to _______
(a) ηd
(b) -ηd
(c) \(\frac{-1}{\eta_{d}}\)
(d) \(\frac{1}{\eta_{d}}\)
Answer:
(c) \(\frac{-1}{\eta_{d}}\)
Hint:
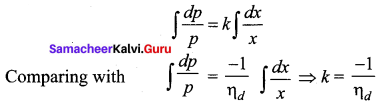
Question 23.
Area bounded by y = ex between the limits 0 to 1 is _________
(a) (e – 1) sq.units
(b) (e + 1) sq.units
(c) (1 – \(\frac{1}{e}\)) sq.units
(d) (1 + \(\frac{1}{e}\)) sq.units
Answer:
(a) (e – 1) sq.units
Hint:
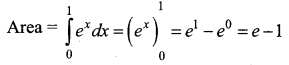
Question 24.
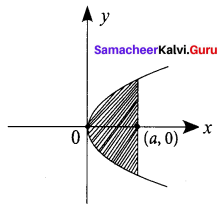
The area bounded by the parabola y2 = 4x bounded by its latus rectum is _______
(a) \(\frac{16}{3}\) sq.units
(b) \(\frac{8}{3}\) sq.units
(c) \(\frac{72}{3}\) sq.units
(d) \(\frac{1}{3}\) sq.units
Answer:
(b) \(\frac{8}{3}\) sq.units
Hint:
y2 = 4x
Comparing with y2 =4ax gives a = 1
Since parabola is symmetric about x – axis,
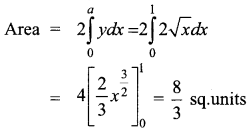
Question 25.
Area bounded by y = |x| between the limits 0 and 2 is _______
(a) 1 sq.units
(b) 3 sq.units
(c) 2 sq.units
(d) 4 sq.units
Answer:
(c) 2 sq.units
Hint:
When x lies between 0 and 2
|x| = x
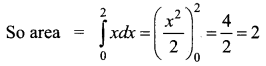
Area = 2 sq.units