Samacheer Kalvi 11th Physics Solutions Chapter 6 Gravitation

Students can Download Physics Chapter 6 Gravitation Questions and Answers, Notes Pdf, Samacheer Kalvi 11th Physics Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 11th Physics Solutions Chapter 6 Gravitation

Samacheer Kalvi 11th Physics Gravitation Textual Evaluation Solved

Samacheer Kalvi 11th Physics Gravitation Multiple Choice Questions

Question 1.
The linear momentum and position vector of the planet is perpendicular to each other at
(a) perihelion and aphelion
(b) at all points
(c) only at parihelion
(d) no point
Answer:
(a) perihelion and aphelion

Question 2.
If the masses of the Earth and Sun suddenly double, the gravitational force between them will
(a) remain the same
(b) increase 2 times
(c) increase 4 times
(d) decrease 2 times
Answer:
(c) increase 4 times
Solution:
The gravitation force of attraction is given by F =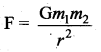
If the masses are doubled then the force will be

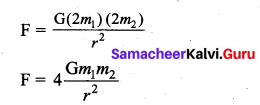
The gravitational force between them will be increase 4 times.

Question 3.
A planet moving along an elliptical orbit is closest to the Sun at distance r₁ and farthest away at a distance of r₂ If V₁ and v₂ are linear speeds at these points respectively. Then the ratio \(\frac{v_{1}}{v_{2}}\) is ……. [NEET 2016]
Answer:
(a) \(\frac{r_{2}}{r_{1}}\)
Solution:
According to the Law of conservation of angular momentum

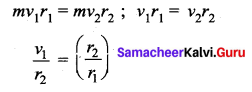
Question 4.
The time period of a satellite orbiting Earth in a circular orbit is independent of ……..
(a) Radius of the orbit
(b) The mass of the satellite
(c) Both the mass and radius of the orbit
(d) Neither the mass nor the radius of its orbit
Answer:
(b) The mass of the satellite

Question 5.
If the distance between the Earth and Sun were to be doubled from its present value, the number of days in a year would be
(a) 64.5
(b) 1032
(c) 182.5
(d) 730
Answer:
(b) 1032
Solution:
By Kepler’s law

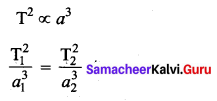
If the distance between the Earth and Sun were to be doubled from its present Value

Question 6.
According to Kepler’s second law, the radial vector to a planet from the Sun sweeps out equal areas in equal intervals of time. This law is a consequence of
(a) conservation of linear momentum
(b) conservation of angular momentum
(c) conservation of energy
(d) conservation of kinetic energy
Answer:
(b) conservation of angular momentum

Question 7.
The gravitational potential energy of the Moon with respect to Earth is
(a) always positive
(b) always negative
(c) can be positive or negative
(d) always zero.
Answer:
(b) always negative

Question 8.
The kinetic energies of a planet in an elliptical orbit about the Sun, at positions A, B and C are K_A, K_B and K_C respectively. AC is the major axis and SB is perpendicular to AC at the position of the Sun S as shown in the figure. Then ….. [NEET 2018]

(a) K_A > K_B > K_C
(b) K_B < K_A < K_C
(c) K_A < K_B < K_C
(d) K_B > K_A > K_C
Answer:
(a) K_A > K_B > K_C
Solution:
The kinetic energy of a planet becomes

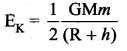
So, kinetic energy is inversly proportional to the orbital distance. Where the distance will be closer E_K is larger and the distance will be larger E_K is less.

Question 9.
The work done by the Sun’s gravitational force on the Earth is ….
(a) always zero
(b) always positive
(c) can be positive or negative
(d) always negative
Answer:
(c) can be positive or negative

Question 10.
If the mass and radius of the Earth are both doubled, then the acceleration due to gravity g1
(a) remains same
(b) \(\frac{g}{2}\)
(c) 2g
(d) 4g
Answer:
(b) \(\frac{g}{2}\)
Solution:
Acceleration due to gravity g’ = \(\frac{\mathrm{GM}}{\mathrm{R}^{2}}\)
If the mass and radius of the Earth are both doubled

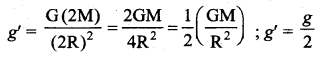
Question 11.
The magnitude of the Sun’s gravitational field as experienced by Earth is …..
(a) same over the year
(b) decreases in the month of January and increases in the month of July
(c) decreases in the month of July and increases in the month of January
(d) increases during day time and decreases during night time.
Answer:
(c) decreases in the month of July and increases in the month of January

Question 12.
If a person moves from Chennai to Trichy, his weight …..
(a) increases
(b) decreases
(c) remains same
(d) increases and then decreases
Answer:
(b) decreases

Question 13.
An object of mass 10 kg is hanging on a spring scale which is attached to the roof of a lift. If
the lift is in free fall, the reading in the spring scale is ……..
(a) 98 N
(b) zero
(c) 49 N
(d) 9.8 N
Answer:
(b) zero
Solution:
The lift is in freefall. It and its contents will experience apparent weightlessness just like astronauts.
The spring balance reading will change from 100 N to zero.

Question 14.
If the acceleration due to gravity becomes 4 times its original value, then escape speed
(a) remains same
(b) 2 times of original value
(c) becomes halved
(d) 4 times of original value
Answer:
(b) 2 times of original value
Solution:
Escape speed 4 times of ‘g’

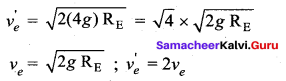
Question 15.
The kinetic energy of the satellite orbiting around the Earth is
(a) equal to potential energy
(b) less than potential energy
(c) greater than kinetic energy
(d) zero
Answer:
(b) less than potential energy

Samacheer Kalvi 11th Physics Gravitation Short Answer Questions

Question 1.
State Kepler’s three laws.
Answer:
1. Law of Orbits: Each planet revolves moves around the Sun in an elliptical orbit with the Sun at one of the foci of the ellipse.
2. Law of area: The radial vector line joining the Sun to a planet sweeps equal areas in equal intervals of time.
3. Law of period: The square of the time period of revolution of a planet around the Sun in its elliptical orbit is directly proportional to the cube of the semi-major axis of the ellipse.

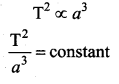
Question 2.
State Newton’s Universal law of gravitation.
Answer:
Newton’s law of gravitation: States that the gravitational force between two masses is directly proportional to product of masses and inversely proportional to square of the distance between the masses.
In the mathematical form, it can be written as,

Question 3.
Will the angular momentum of a planet be conserved? Justify your answer.
Answer:
The triumph of the law of gravitation is that it concludes that the mango that is falling down and the Moon orbiting the Earth are due to the same gravitational force.

Question 4.
Define the gravitational field. Give its unit.
The gravitational field intensity \(\overrightarrow{\mathrm{E}}_{1}\) at a point is defined as the gravitational force experienced by unit mass at that point. It’s unit N kg^-1.

Question 5.
What is meant by superposition of gravitational field?
Answer:
The total gravitational field at a point due to all the masses is given by the vector sum of the gravitational field due to the individual masses. This principle is known as superposition of gravitational fields.

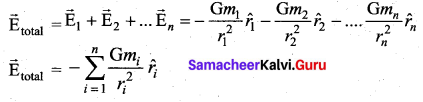
Question 6.
Define gravitational potential energy.
Answer:
Potential energy of a body at a point in a gravitational field is the work done by an external agent in moving the body from infinity to that point.

Question 7.
Is potential energy the property of a single object? Justify.
Answer:
There is no potential energy for a single object. The gravitational potential energy depends upon the two masses and the distance between them.

Question 8.
Define gravitational potential.
Answer:
The gravitational potential is defined as the amount of work required to bring unit mass from infinity to that point.

Question 9.
What is the difference between gravitational potential and gravitational potential energy?
Answer:

Gravitational Potential	Gravitational potential Energy
The amount of work required to bring unit mass from infinity to that point in point an gravitational field.	The work done by an external agent in moving the body from infinity to that in an gravitational field.
The unit of V(r) is J kg-1	The unit of U(r) is J (or) joule.

Question 10.
What is meant by escape speed in the case of the Earth?
Answer:
The escape speed is independent of the direction in which the object is thrown. Irrespective of whether the object is thrown vertically up, radially outwards or tangentially it requires the same initial speed to escape Earth’s gravity force. This can be written as, v_e = \(\sqrt{2 g R_{E}}\).

Question 11.
Why is the energy of a satellite (or any other planet) negative?
Answer:
The energy of satellite is negative. Because the energy implies that the satellite is bound to the Earth by means of the attractive gravitational force.

Question 12.
What are geostationary and polar satellites?
Answer:
Geostationary Satellite: It is the satellite which appears at a fixed position and at a definite height to an observer on earth.
Polar Satellite: It is the satellite which revolves in polar orbit around the earth.

Question 13.
Define weight.
Answer:
The weight of an object \(\overrightarrow{\mathrm{W}}\) is defined as the downward force whose magnitude W is equal to that of upward force that must be applied to the object to hold it at rest or at constant velocity relative to the earth. The direction of weight is in the direction of gravitational force. So the magnitude of weight of an object is denoted as, W = N = mg.

Question 14.
Why is there no lunar eclipse and solar eclipse every month?
Answer:
If the orbits of the Moon and Earth lie on the same plane, during full Moon of every month, we can observe lunar eclipse. If this is so dining new Moon we can observe solar eclipse. But Moon’s orbit is tilted 5° with respect to Earth’s orbit. Due to this 5° tilt, only during certain periods of the year, the Sun, Earth and Moon align in straight line leading to either lunar eclipse or solar eclipse depending on the alignment.

Question 15.
How will you prove that Earth itself is spinning?
Answer:
The Earth’s spinning motion can be proved by observing star’s position over a night. Due to Earth’s spinning motion, the stars in sky appear to move m circular motion about the pole star.

Samacheer Kalvi 11th Physics Gravitation Long Answer Questions

Question 1.
Discuss the important features of the law of gravitation.
Answer:
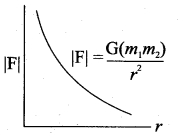
1. As the distance between two masses increases, the strength of the force tends to decrease because of inverse dependence on r². Physically it implies that the planet Uranus experiences less |F| gravitational force from the Sun than the Earth since Uranus is at larger distance from the Sun compared to the Earth.
2. The gravitational forces between two particles always constitute an action-reaction pair. It implies that the gravitational force exerted by the Sim on the Earth is always towards the Sun. The reaction-force is exerted by the Earth on the Sun. The direction of this reaction force is towards Earth.

3. The torque experienced by the Earth due to the gravitational force of the Sun is given by

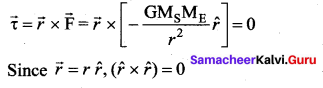
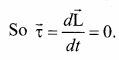. It implies that angular momentum \(\overrightarrow{\mathrm{L}}\) is a constant vector.

4. The expression 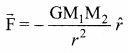has one inherent assumption that both M₁, and M₂ are treated as point masses. When it is said that Earth orbits around the Sun due to Sun’s gravitational force, we assumed Earth and Sun to be point masses.
5. Point masses holds even for small distance.
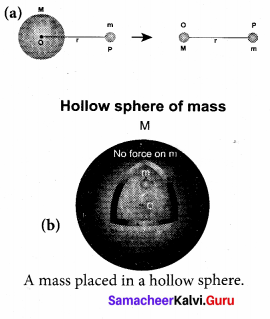
6. There is also another interesting result. Consider a hollow sphere of mass M. If we place another object of mass ‘m’ inside this hollow sphere the force experienced by this mass ‘m’ will be zero.

Question 2.
Explain how Newton arrived at his law of gravitation from Kepler’s third law.
Answer:
Newton law of gravitation states that a particle of mass M₁ attracts any other particle of mass M₂ in the universe with an attractive force. The strength of this force of attraction was found to be directly proportional to the product of their masses and is inversely proportional to the square to the distance between them. In mathematical form, it can be written as:

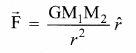
where \(\hat{r}\) is the unit vector from M₁ towards M₂ as shown in given figure, and G is the Gravitational constant that has the value of 6.67 × 10^-11 N m² kg^-2, and r is the distance between the two masses M₁ and M₂.

In given figure the vector \(\overrightarrow{\mathrm{F}}\) denotes the gravitational force experienced by M₂ due to M₁. Here the negative sign indicates that the gravitational force is always attractive in nature and the direction of the force is along the line joining the two masses. In Cartesian coordinates, the square of the distance is expressed as r² = (x² + y² + z²)

Question 3.
Explain how Newton verified his law of gravitation.
Answer:
Newton inverse square law: Newton considered the orbits of the planets as circular. For circular orbit of radius r, the centripetal acceleration towards the centre is


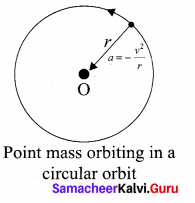
The velocity in terms of known quantities r and T, is

Here T is the time period of revolution of the planet. Substituting this value of v in equation (1) we get,

Substituting the value ‘a’ from (3) in Newton’s second law, F = ma, where ‘m’ is the mass of the planet.

By substituting equation (6) in the force expression, we can arrive at the law of gravitation.

Here negative sign implies that the force is attractive and it acts towards the center. But Newton strongly felt that according to his third law, if Earth is attracted by the Sun, then the Sim must also be attracted by the Earth with the same magnitude of force. So he felt that the Sun’s mass (M) should also occur explicitly in the expression for force (7). From this insight, he equated the constant 4π²k to GM which turned out to be the law of gravitation.

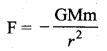
Again the negative sign in the above equation implies that the gravitational force is attractive.

Question 4.
Derive the expression for gravitational potential energy.
Answer:
The gravitational force is a conservative force and hence we can define a gravitational potential energy associated with this conservative force field.
Two masses m₁ and m₂ are initially separated by a distance r’. Assuming m₁ to be fixed in its position, work must be done on m₂ to move the distance from r’ to r.

To move the mass m₂ through an infinitesimal displacement \(d \vec{r}\) from \(\vec{r}\) to \(\vec{r}\) + \(d \vec{r}\), work has to be done externally. This infinitesimal work is given by

The work is done against the gravitational force, therefore,

Substituting equation (2) in (1), we get

Thus the total work for displacing the particle from r’ to r is

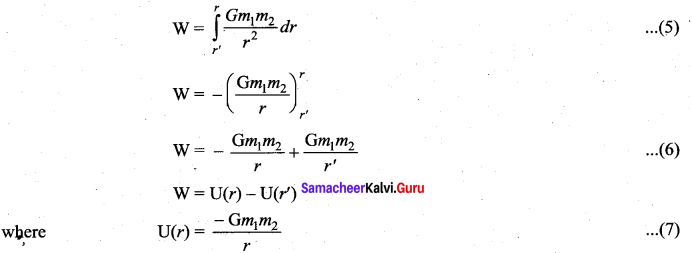
This work done W gives the gravitational potential energy difference of the system of masses m₁ and m₂ when the seperation between them are r and r’ respectively.

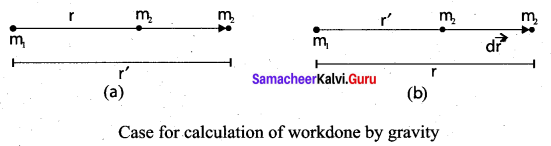
Case 1: If r < r’ : Since gravitational force is attractive, m₂ is attracted by m₁. Then m₂ can move from r’ to r without any external Work. Here work is done by the system spending its internal energy and hence the work done is said to be negative.
Case 2: If r > r’: Work has to be done against gravity to move the object from r’ to r. Therefore work is done on the body by external force and hence work done is positive.

Question 5.
Prove that at points near the surface of the Earth, the gravitational potential energy of the object is U = mgh.
Answer:
When an object of mass m is raised to a height h, the potential energy stored in the object is mgh. This can be derived using the general expression for gravitational potential energy.
Consider the Earth and mass system, with r, the distance between the mass m and the Earth’s centre. Then the gravitational potential energy.

Here r = R_e + h, where R_e is the radius of the Earth, h is the height above the Earth’s surface


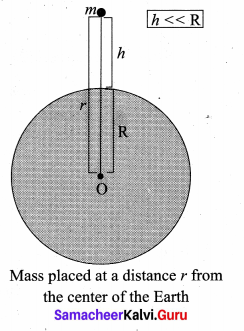
Substituting equation (4) and (5) we get,
U = -mg_e + mgh …….. (6)
It is clear that the first term in the above expression is independent of the height h. For example, if the object is taken from height h₁ to h₂, then the potential energy at h₁ is
U(h₁) = – mgR_e + mgh₁ …(7)
and the potential energy at h₂ is
U(h₂) = – mgR_e + mgh₂ …(8)
The potential energy difference between h₁ and h₂ is
U(h₂) – U(h₁) = mg(h₂ – h₁) …(9)
The term mgR_e in equation (7) and (8) plays no role in the result. Hence in the equation (6) the first term can be omitted or taken to zero. Thus it can be stated that the gravitational potential energy stored in the particle of mass m at a height h from the surface of the Earth is U = mgh. On the surface of the Earth, U = 0, since h is zero.

Question 6.
Explain in detail the idea of weightlessness using lift as an example.
Answer:
When a man is standing in the elevator, there are two forces acting on him.
1. Gravitational force which acts downward. If we take the vertical direction as positive y direction, the gravitational force acting on the man is \(\overrightarrow{\mathrm{F}}_{\mathrm{G}}=-m \hat{g} \hat{j}\)
2. The normal force exerted by floor on the man which acts vertically upward, \(\overrightarrow{\mathrm{N}}=\mathrm{N} \hat{j}\)
Weightlessness of freely falling bodies: Freely falling objects experience only gravitational force. As they fall freely, they are not in contact with any surface (by neglecting air friction). The normal force acting on the object is zero. The downward acceleration is equal to the acceleration due to the gravity of the Earth, i.e., (a = g)
Newton’s 2nd law acting on the man N = m(g – a)
a = g ∴ N = m(g – g) = 0.

Question 7.
Derive an expression for escape speed.
Answer:
Consider an object of mass M on the surface of the Earth. When it is thrown up with an initial speed v_i, the initial total energy of the object is

where, M_E is the mass of the Earth and R_E the radius of the Earth. The term 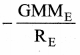is the potential energy of the mass M.
When the object reaches a height far away from Earth and hence treated as approaching infinity, the gravitational potential energy becomes zero [U(∞) = 0] and the kinetic energy becomes zero as well. Therefore the final total energy of the object becomes zero. This is for minimum energy and for minimum speed to escape. Otherwise kinetic energy can be nonzero.
E_f = 0
According to the law of energy conservation,
E_i = E_f …. (2)
Substituting (1) in (2) we get,

Consider the escape speed, the minimum speed required by an object to escape Earth’s gravitational field, hence replace v_i with v_e, i.e.,

From equation (4) the escape speed depends on two factors acceleration due to gravity and radius of the Earth. It is completely independent of the mass of the object. By substituting the values of g (9.8 ms^-2) and R_e = 6400 km, the escape speed of the Earth is v_e = 11.2 kms^-1. The escape speed is independent of the direction in which the object is thrown. Irrespective of whether the object is thrown vertically up, radially outwards or tangentially it requires the sarfte initial speed to escape Earth’s gravity.

Question 8.
Explain the variation of g with latitude.
Answer:
When an object is on the surface for the Earth, it experiences a centrifugal force that depends on the latitude of the object on Earth. If the Earth were not spinning, the force on the object would have been mg. However, the object experiences an additional centrifugal force due to spinning of the Earth.
This centrifugal force is given by mω²R’.


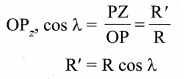
where λ is the latitude. The component of centrifugal acceleration experienced by the object in the direction opposite to g is
a_PQ = ω²R’ cos λ = ω²R cos² λ
Since R’ = R cos λ
Therefore, g’ = g – ω² R cos² λ
From the above expression, we can infer that at equator, λ = 0, g’ = g – ω²R. The acceleration due to gravity is minimum. At poles λ = 90; g’ = g, it is maximum. At the equator, g’ is minimum.

Question 9.
Explain the variation of g with altitude from the Earth’s surface.
Answer:
Consider an object of mass m at a height h from the surface of the Earth. Acceleration experienced by the object due to Earth is

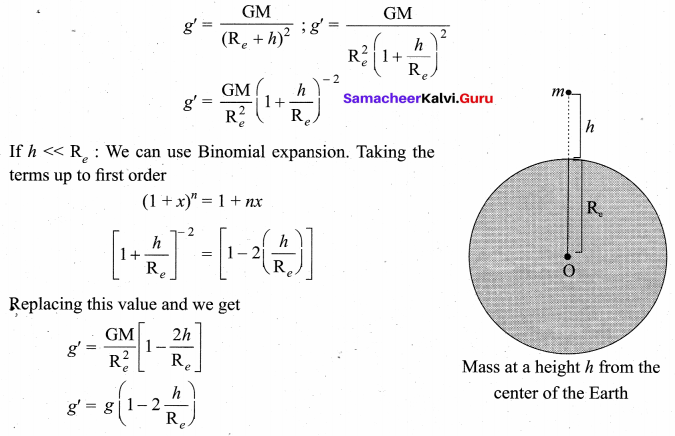
We find that g’ < g. This means that as altitude h increases the acceleration due to gravity g decreases.

Question 10.
Explain the variation of g with depth from the Earth’s surface.
Answer:
Consider a particle of mass m which is in a deep mine on the Earth. (Example: coal mines in Neyveli). Assume the depth of the mine as d. To calculate g’ at a depth d, consider the following points.
The part of the Earth which is above the radius (R_e – d) do not contribute to the acceleration. The result is proved earlier and is given as

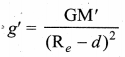
Here M’ is the mass of the Earth of radius (R_e – d)
Assuming the density of Earth ρ to be constant, \(\rho=\frac{M}{V}\)
where M is the mass of the Earth and V its volume, thus,


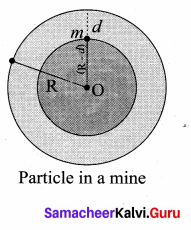
Here also g’ < g. As depth increase, g’ decreases. It is very interesting to know that acceleration due to gravity is maximum on the surface of the Earth but decreases when we go either upward or downward.

Question 11.
Derive the time period of satellite orbiting the Earth.
Answer:
Time period of the satellite: The distance covered by the satellite during one rotation in its orbit is equal to 2π(R_E + h) and time taken for it is the time period, T. Then,


Squaring both sides of the equation (2) we get

Equation (3) implies that a satellite orbiting the Earth has the same relation between time and distance as that of Kepler’s law of planetary motion. For a satellite orbiting near the surface of the Earth, h is negligible compared to the radius of the Earth R_E. Then,

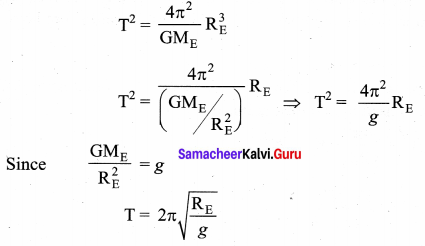
By substituting the values of R_E = 6.4 × 10⁶ m and g = 9.8ms^-2, the orbital time period is obtained as T ≅ 85 minutes.

Question 12.
Derive an expression for energy of satellite.
Answer:
The total energy of the satellite is the sum of its kinetic energy and the gravitational potential energy. The potential energy of the satellite is,

Here M_s – mass of the satellite, M_E -mass of the Earth, R_E – radius of the Earth.
The Kinetic energy of the satellite is

Here v is the orbital speed of the satellite and is equal to

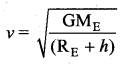
Substituting the value of v in (2) the kinetic energy of the satellite becomes,

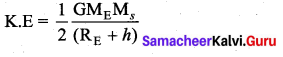
Therefore the total energy of the satellite is

The negative sign in the total energy implies that the satellite is bound to the Earth and it cannot escape from the Earth.
Note: As h approaches ∞, the total energy tends to zero. Its physical meaning is that the satellite is completely free from the influence of Earth’s gravity and is not bound to Earth at large distance.

Question 13.
Explain in detail the geostationary and polar satellites.
Answer:
The satellites orbiting the Earth have different time periods corresponding to different orbital radii. Kepler’s third law is used to find then radius of the orbit.

Substituting for the time period (24 hours = 86400 seconds), mass, and radius of the Earth, h turns out to be 36,000 km. Such satellites are called “geo-stationary satellites”, since they appear to be stationary when seen from Earth.

India uses the INSAT group of satellites that are basically geo-stationary satellites for the purpose of telecommunication. Another type of satellite which is placed at a distance of 500 to 800 krn from the surface of the Earth orbits the Earth from north to south direction. This type of satellite that orbits Earth from North Pole to South Pole is called a polar satellite. The time period of a polar satellite is nearly 100 minutes and the satellite completes many revolutions in a day. A polar satellite covers a small strip of area from pole to pole during one revolution. In the next revolution it covers a different strip of area since the Earth would have moved by a small angle. In this way polar satellites cover the entire surface area of the Earth.

Question 14.
Explain how geocentric theory is replaced by heliocentric theory using the idea of retrograde motion of planets.
Answer:
When the motion of the planets are observed in the night sky by naked eyes over a period of a few months, it can be seen that the planets move eastwards and reverse their motion for a while and return to eastward motion again. This is called “retrograde motion of planets.

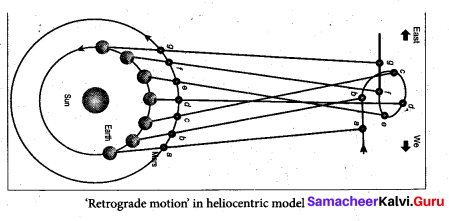
Careful observation for a period of a year clearly shows that Mars initially moves eastwards (February to June), then reverses its path and moves backwards (July, August, September). It changes it direction of motion once again and continues its forward motion (October onwards). In olden days, astronomers recorded the retrograde motion of all visible planets and tried to explain the motion. According to Aristotle, the other planets and the Sun move around the Earth in the circular orbits. If it was really a circular orbit it was not known how the planet could reverse its motion for a brief interval. To explain this retrograde motion, Ptolemy introduced the concept of “epicycle” in his geocentric model. According to this theory, while the planet orbited the Earth, it also underwent another circular motion termed as “epicycle’. A combination of epicycle and circular motion around the Earth gave rise to retrograde motion of the planets with respect to Earth. Essentially Ptolemy retained the Earth centric idea of Aristotle and added the epicycle motion to it.

But Ptolemy’s model became more and more complex as every planet was found to undergo retrograde motion. In the 15th century, the Polish astronomer Copernicus proposed the heliocentric model to explain this problem in a simpler manner. According to this model, the Sun is at the centre of the solar system and all planets orbited the Sun. The retrograde motion of planets with respect to Earth is because of the relative motion of the planet with respect to Earth.
Earth orbits around the Sun faster than Mars. Because of the relative motion between Mars and Earth, Mars appears to move backwards from July to October. In the same way the retrograde motion of all other planets was explained successfully by the Copernicus model. It was because of its simplicity, the heliocentric model slowly replaced the geocentric model.

Question 15.
Explain in detail the Eratosthenes method of finding the radius of Earth.
Answer:
Eratosthenes observed that during noon time of summer solstice the Sun’s rays cast no shadow in the city Syne which was located 500 miles away from Alexandria. At the same day and same time he found that in Alexandria the Sun’s rays made 7.2 degree with local vertical. He realized that this difference of 7.2 degree was due to the curvature of the Earth.

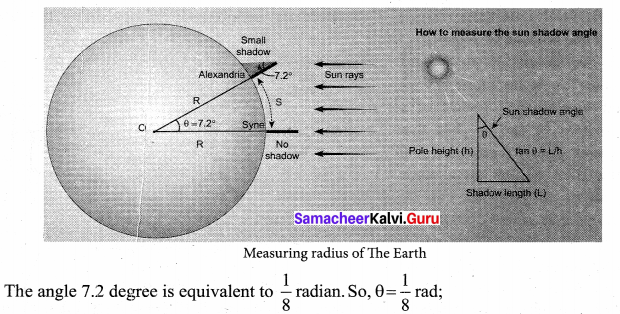
If S is the length of the arc between the cities of Syne and Alexandria, and if R is radius of Earth, then

1 mile is equal to 1.609 km. So, he measured the radius of the Earth to be equal to R = 6436 km, which is amazingly close to the correct value of 6378 km.

Question 16.
Describe the measurement of Earth’s shadow (umbra) radius during total lunar eclipse.
Answer:
Lunar eclipse and measurements of shadow of Earth: On January 31, 2018 there was a total lunar eclipse which was observed from various place including Tamil Nadu. It is possible to measure the radius of shadow of the Earth at the point where the Moon crosses.

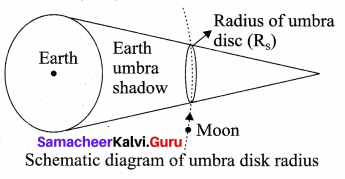
When the Moon is inside the umbra shadow, it appears red in colour. As soon as the Moon Schematic diagram of umbra disk radius exits from the umbra shadow, it appears in crescent shape.

By finding the apparent radii of the Earth’s umbra shadow and the Moon, the ratio of the these radii can be calculated.
The apparent radius of Earth’s umbra shadow = R_s = 13.2 cm
The apparent radius of the Moon = R_m = 5.15 cm

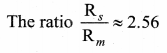
The radius of Moon R_m = 1737 km
The radius of the Earth’s umbra shadow is R_s = 2.56 × 1737 km ≅ 4446
The correct radius is 4610 km

The error will reduce if the pictures taken using a high quality telescope are used.

Samacheer Kalvi 11th Physics Gravitation Conceptual Questions

Question 1.
In the following what are the quantities which that are conserved?
(a) Linear momentum of planet
(b) Angular momentum of planet
(c) Total energy of planet
(d) Potential energy of a planet
Answer:
Since there is a net force acting on the planet, its velocity changes which means its linear momentum changes. In fact, the absolute value of linear momentum changes too since the planet’s speed is variable as it goes around in its elliptical orbit . So the linear momentum of planet is not conserved. But the angular momentum about the sun is conserved. Since the torque of gravitational force is zero.

The total mechanical energy remains constant for an isolated system objects that interact with conservative forces. So, the total energy of the system of planet is conserved. The single energy of the planet is not conserved.

Question 2.
The work done by Sun on Earth in one year will be
(a) Zero
(b) None zero
(c) positive
(d) negative
Answer:
(a) Zero

Question 3.
The work done by Sun on Earth at any finite interval of time is
(a) positive, negative or zero
(b) Strictly positive
(c) Strictly negative
(d) It is always zero
Answer:
(d) It is always zero
2 & 3. No work is done on the earth revolving around it in perfectly circular orbit. The earth revolves around the sun due to gravitational force of attraction between the sun and the earth. This force around the sun. This centripetal force is always perpendicular to the linear displacement.
Work done = W = F.d cos θ Since θ = 90°

Question 4.
If a comet suddenly hits the Moon and imparts energy which is more than the total energy of the Moon, what will happen?
Answer:
A comet with small velocity and high mass, doesn’t trigger the moon much. It just makes a circular shaped impact. The moon is ment for the protection for life on earth and to attain stability for the earth rotation. But a comet with large mass and with large velocity may destroy the moon completely or its impact makes the moon, go out of its orbit.

Question 5.
If the Earth’s pull on the Moon suddenly disappears, what will happen to the Moon?
Answer:
Basically, the moon would become the third planet, however the orbit may change. The moon is in orbit around the earth, and what happens will depend on just when the earth disappears. The moon travels around the earth at about 1 km/sec and the Earth – moon pair travel around the sun at about 30 km/sec. This extra 1 km/sec movement will result in an orbit change.

Question 6.
If the Earth has no tilt, what happens to the seasons of the Earth?
Answer:
If the earth weren’t tilted on its axis, there would be no seasons. And humanity would suffer.

Question 7.
A student was asked a question ‘why are there summer and winter for us? He replied as ‘since Earth is orbiting in an elliptical orbit, when the Earth is very faraway from .the Sun (aphelion) there will be winter, when the Earth is nearer to the Sun (perihelion) there will be winter}. Is this answer correct? If not, what is the correct explanation for the occurrence of summer and winter?
Answer:
Early astronomers proved that Earth is spherical in shape by looking at the shape of the shadow cast by Earth on the Moon during lunar eclipse.

Question 8.
The following photographs are taken from the recent lunar eclipse which occurred on January 31, 2018. Is it possible to prove that Earth is a sphere from these photographs?
Answer:
Early astronomers proved that Earth is spherical in shape by looking at the shape of the shadow cast by Earth on the Moon during lunar eclipse.

Samacheer Kalvi 11th Physics Gravitation Numerical Problems

Question 1.
An unknown a planet orbits the Sun with distance twice the semi major axis distance of the Earth’s orbit. If the Earth’s time period is Tp what is the time period of this unknown planet?
Answer:
By Kepler’s 3rd law T² ∝ a³
Time period of unknown planet = T₂
Time period of Earth = T₁
Distance of unknown planet from the Sun = a₂
Distance of the Earth from the Sun = a₁

Question 2.
Assume that you are in another solar system and provided with the set of data given below consisting of the planets’ semi major axes and time periods. Can you infer the relation connecting semi major axis and time period?
Answer:

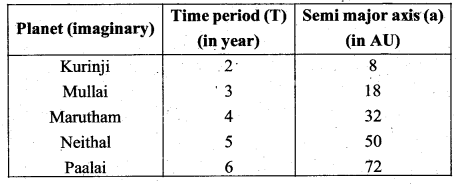
In a given datas tells us the relation connecting to the semi major axis is proportional to the two times of square of the time period.
a ∝ 2T²

Question 3.
If the masses and mutual distance between the two objects are doubled, what is the change in the gravitational force between them?
Answer:
By Newton’s law of gravitation

Here, the masses and mutual distance between the two objects are doubled .

There is no change in the gravitational force between them.

Question 4.
Two bodies of masses m and 4m are placed at a distance r. Calculate the gravitational potential at a point on the line joining them where the gravitational field is zero.
Answer:
Let the point be the position when the gravitational field is zero.,

The point P is at a distance \(\frac{r}{3}\) from mass ‘m’ and \(\frac{2r}{3}\) from mass ‘4m’

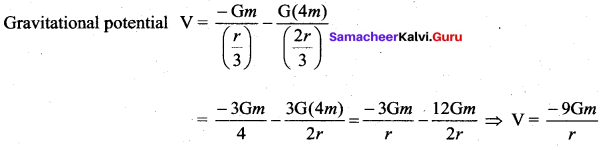
Question 5.
If the ratio of the orbital distance of two planets \(\frac{d_{1}}{d_{2}}\) = 2, what is the ratio of gravitational field experienced by these two planets?
Answer:
The gravitational field experienced by planets 1

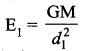
The gravitational field experienced by planet 2

Question 6.
The moon I_o orbits Jupiter once in 1.769 days. The orbital radius of the Moon I₀ is 421700 km. Calculate the mass of Jupiter?
Answer:
Kepler’s third law is used to find the mass of the planet

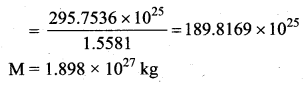
Question 7.
If the angular momentum of a planet is given by \(\overrightarrow{\mathbf{L}}=5 t^{2} \hat{i}-6 \hat{t} \hat{j}+3 \hat{k}\). What is the torque experienced by the planet? Will the torque be in the same direction as that of the angular momentum?
Answer:
The torque experienced by the planet

Question 8.
Four particles, each of mass M and equidistant from each other, move along a circle of radius R under the action of their mutual gravitational attraction. Calculate the speed of each particle.
Answer:
The net gravitational force = Centripetal force

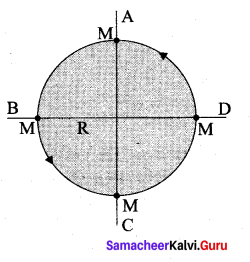
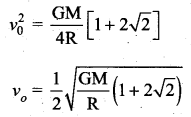
Question 9.
Suppose unknowingly you wrote the universal gravitational constant value as G = 6.67 × 10¹¹ instead of the correct value G = 6.67 × 10^-11, what is the acceleration due to gravity g’ for this incorrect G? According to this new acceleration due to gravity, what will be your weight W?
Answer:
Data: Incorrect Gravitational constant G = 6.67 × 10¹¹ Nm² kg^-2
Mass of the Earth M_e = 5.972 × 10²⁴ kg
Radius of the earth R_e = 6371 km (or) 6371 × 10³ m

Question 10.
Calculate, the gravitational field at point O due to three masses m₁, m₂, and m₃ whose positions are given by the following figure. If the masses m₁ and m₂ are equal what is the change in gravitational field at the point O?
Answer:

(Negative sign indicates field acting along negative x direction)

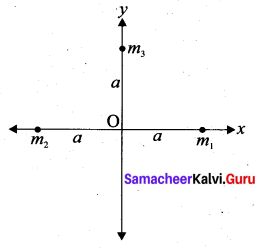
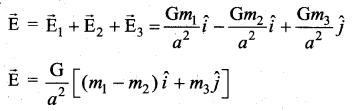
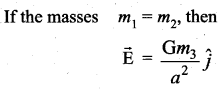
Question 11.
What is the gravitational potential energy of the Earth and Sun? The Earth to Sun distance is around 150 million km. The mass of the Earth is 5.9 × 10²⁴ kg and mass of the Sun is 1.9 × 10³⁰ kg.
Answer:
Mass of the Earth M_E = 5.9 × 10²⁴ kg
Mass of the Sun M_S = 1.9 × 10³⁰ kg
Distance between the Sun and Earth
r = 150 million km; r = 150 × 10⁹ m
Gravitational constant G = 6.67 × 10^-11 Nm² kg^-2
The gravitational potential energy

Question 12.
Earth revolved around the Sun at 30 km s^-1. Calculate the kinetic energy of the Earth. In the previous example you calculated the potential energy of the Earth. What is the total energy of the Earth in that case? Is the total energy positive? Give reasons.
Answer:
Mass of the Earth M_E = 5.9 × 10²⁴ kg
Speed of the Earth rovolves around the Sun

= 2.655 × 10³³ + (- 4.985 × 10³³)
= 2.655 × 10³³ – 4.985 × 10³³
E = -2.33 × 10³³ joule (or) J
‘-Ve’ implies that Earth is bounded with Sun.

Question 13.
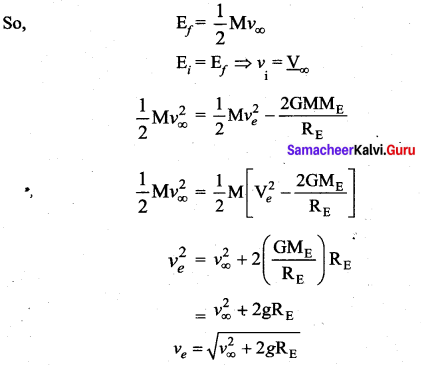
An object is thrown from Earth in such a way that it reaches a point at infinity with non-zero kinetic energy 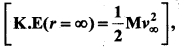with that velocity should the object be thrown from Earth?
Answer:
An object is thrown up with an initial velocity is v_i, So Total energy of the object is

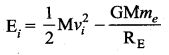
Now, the object reaches a height with a non-zero K.E.
K.E becomes infinity. P.E becomes zero.

Question 14.
Suppose we go 200 km above and below the surface of the Earth, what are the g values at these two points? In which case, is the value of g small?
Answer:
Variation of g’ with depth

Variation of g’ with altitude

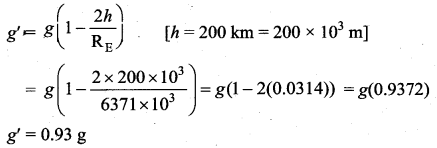
Question 15.
Calculate the change in g value in your district of Tamil Nadu. (Hint: Get the latitude of your district of Tamilnadu from the Google). What is the difference in g values at ‘ Chennai and Kanyakumari?
Answer:
Variation of ‘g’ value in the latitude to chennai

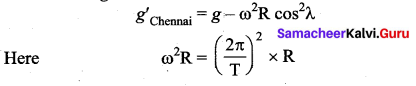
Period of revolution (T) = 1 day = 86400 sec
Radius of the Earth (R) = 6400 × 10³ m
Latitude of Chennai (λ) = 13° = 0.2268 rad

Variation of ‘g’ value in the latitude of Kanyakumari

Samacheer Kalvi 11th Physics Gravitation Additional Questions

I. Choose the correct answer from the following:

Question 1.
According to Kepler, planet move in
(a) Circular orbits around the Sun
(b) Elliptical orbits around the Sim with Sun at exact centre
(c) Straight lines with constant velocity ‘
(d) Elliptical orbits around the Sun with Sun at one of its foci.
Answer:
(d) Elliptical orbits around the Sun with Sun at one of its foci.

Question 2.
Kepler’s second law regarding constancy of aerial velocity of a planet is consequence of the law of conservation of ………
(a) energy
(b) angular momentum
(c) linear momentum
(d) None of these
Answer:
(b) angular momentum
Hint:

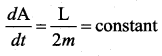
Question 3.
According to Kepler, the period of revolution of a planet (T) and its mean distance from the Sun (a) are related by the equation
(a) T³ a³ = constant
(b) T² a^-3 = constant
(c) Ta³ = constant
(d) T²a = constant
Answer:
(b) T² a^-3 = constant
Hint:

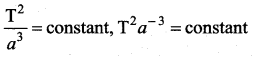
Question 4.
The period of Moon’s rotation around the Earth is nearly 29 days. If Moon’s mass were 2 fold
its present value and all other things remained unchanged the period of Moon’s rotation would be nearly ….. days.

Answer:
(d) 29
Hint:
Time period does not depends upon the mass of satellite.

Question 5.
The period of revolution of planet A around the Sun is 8 times that of B. The distance of A from the Sun is how many times greater than that of B from the Sun.
(a) 2
(b) 3
(c) 4
(d) 5
Answer:
(c) 4
Hint:

Question 6.
The radius of orbit of a planet is two times that of Earth. The time period of planet is years …….
(a) 4.2
(b) 2.8
(c) 5.6
(d) 8.4
Answer:
(b) 2.8
Hint:

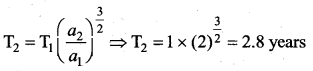
Question 7.
A geostationary satellite orbits around the earth in a circular orbit of radius 3600 km the time period of a satellite orbiting a few hundred kilometers above the earth’s surface (R_E = 6400 km) will be approximately be …… hours.
(a) 1/2
(b) 1
(c) 2
(d) 4
Answer:
(c) 2
Hint:

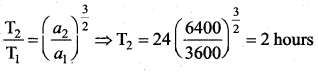
Question 8.
What does not change in the field of central force?
(a) Potential energy
(b) kinetic energy
(c) linear momentum
(d) Angular momentum
Answer:
(d) Angular momentum
Hint:
For central force torque is zero.

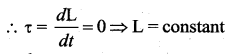
Question 9.
A satellite which is geostationary in a particular orbit is taken to another orbit. Its distance from the center of earth in new orbit is two times of the earlier orbit. The time period in second orbit is …… hours.

Answer:
(b) \(48 \sqrt{2}\)
Hint:

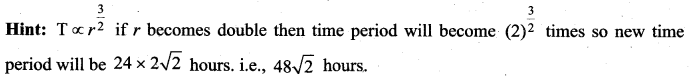
Question 10.
If the Earth is at one-fourth of its present distance from the sun the duration of year will be:
(a) half the present year
(b) one-eight the present year
(c) one-fourth the present year
(d) one-sixth the present year
Answer:
(b) one-eight the present year
Hint:

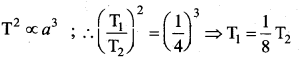
Question 11.
The Earth E moves in an elliptical orbit with the Sun S at one of the foci as shown in figure.
Its speed of motion will be maximum at a point ……..

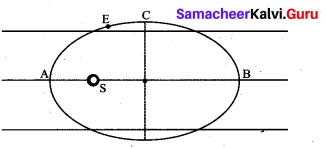
(a) C
(b) A
(c) B
(d) D
Answer:
(b) A
Hint: Speed at the Earth will be maximum when its distance from the Sun is minimum because
mvr = constant

Question 12.
Rockets are launched in eastward direction to take advantage of …..
(a) the clear sky on eastern side
(b) Earth’s rotation
(c) the thinner atmosphere on this side
(d) Earth’s tilt
Answer:
(b) Earth’s rotation
Hint:
Because Earth rotation from west to east direction.

Question 13.
Two sphere of mass M₁ and M₂ are situated in air and the gravitational force between them is F. The space around the masses is now filled with liquid of specific gravity 3. The gravitational force will now be ……

Answer:
(a) F
Hint:
Gravitational force does not depend upon the medium.

Question 14.
Which of the following statement about the gravitational constant is true?
(a) It is a force
(b) It has same value in all system of unit
(c) It has not unit
(d) It depends on the value of the masses
Answer:
(a) It is a force

Question 15.
Energy required to move a body of mass ‘M’ from an orbit of radius 2R to 3R is …….

Answer:
(d) \(\frac{\mathrm{GMm}}{6 \mathrm{R}}\)
Hint:
Change in P.E. in displacing a body from r₁ and r₂ is given by:

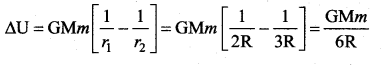
Question 16.
The mass of the earth is 6 × 10²⁴ kg and that of the Moon is 7.4 × 10²² kg. The constant of gravitation G is 6.67 × 10^-11 Nm² kg^-2. The potential energy of the system is – 7.79 × 10²⁸J. The mean distance between the Earth and Moon is …… metre.
(a) 3.80 × 10⁸
(b) 3.37 × 10⁸
(c) 7.60 × 10⁸
(d) 1.90 × 10²
Answer:
(a) 3.80 × 10⁸
Hint:

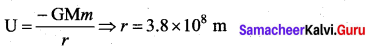
Question 17.
What is the intensity of gravitational field at the center of spherical shell?
(a) \(\frac{\mathrm{G} m}{r^{2}}\)
(b) g
(c) zero
(d) None of these
Answer:
(c) zero

Question 18.
A body of mass m is taken from the Earth’s surface to a height equal to the radius R of the earth. If g is the acceleration to gravity at the surface of the Earth, then find the change in the potential energy of the body ……

Answer:
(b) \(\frac{1}{2} m g R\)
Hint:

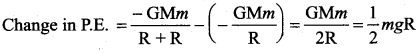
Question 19.
A satellite is orbiting around the Earth in a circular orbit with velocity v. If m is the mass of the satellite, its total energy is ……

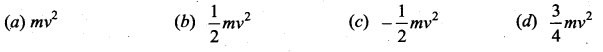
Answer:

Hint:
The total energy is negative of the kinetic energy.

Question 20.
Escape velocity of a body of 1 kg. On a planet is 100 ms^-1. Gravitational potential energy of the body at the planet is ……
(a) -5000 J
(b) – 1000 J
(c) – 2400 J
(d) 4000 J
Answer:
(a) – 5000 J

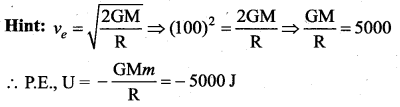
Question 21.
A particle falls towards earth from infinity. It’s velocity reaching the Earth would be ……

Answer:
(b) \(\sqrt{2 g \mathrm{R}}\)
Hint:
This should be equal to escape velocity is = \(\sqrt{2 g \mathrm{R}}\)

Question 22.
An artificial satellite is revolving round the Earth in a circular orbit, its velocity is half the escape velocity. Its height from the Earth surface is …. km.
(a) 6400
(b) 12800
(c) 3200
(d) 1600
Answer:
(a) 6400

Question 23.
The escape velocity of a body on the surface of the Earth is 11.2 km/s. If the mass of the Earth is increase to twice its present value and the radius of the earth becomes half, the escape velocity becomes = …… kms^-1
(a) 5.6
(b) 11.2
(c) 22.4
(d) 494.8
Answer:
(c) 22.4
Hint:

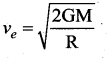
If M becomes double and R becomes half, then escape velocity becomes two times.

Question 24.
The velocity with which a projectile must be fired so that it escapes Earth’s gravitational does
not depend on ……..
(a) Mass of Earth
(b) Radius of the projectile’s orbit
(c) Mass of the projectile
(d) Gravitational constant
Answer:
(c) Mass of the projectile

Question 25.
The escape velocity for a body projected vertically upwards from the surface of Earth is 11 kms^-1. If the body is projected at an angle of 45° with the vertical, the escape velocity will be …. kms^-1

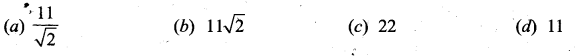
Answer:
(d) 11
Hint:
Escape velocity does not depends upon the angle of projection.

Question 26.
Two satellites of mass ml and m₂(m₁> m₂) are revolving round the earth in circular orbits of r₁ and r₂ (r₁ > r₂) respectively. Which of the following statement is true regarding their speeds v₁ and v₂ ……..

Answer:
(b) v₁ < v₂
Hint:

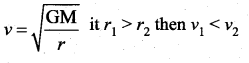
Question 27.
As astronaut orbiting the earth in a circular orbit 120 km above the surface of Earth, gently drops a spoon out of space-ship. The spoon will ……….
(a) fall vertically down to the Earth
(b) move towards the moon
(c) will move along with space-ship
(d) will move in an irregular way then fall down to Earth
Answer:
(c) will move along with space-ship
Hint:
The velocity of the spoon will be equal to the orbital velocity when dropped out of the space-ship

Question 28.
A satellite revolves around the Earth in an elliptical orbit. Its speed.
(a) is the same at all point in the orbit
(b) is greatest when it is closest to the Earth
(c) is greatest when it is farthest to the Earth
(d) goes on increasing or decreasing continuously depending upon the mass of the satellite. Answer:
(b) is greatest when it is closest to the Earth

Question 29.
A satellite is moving around the Earth with speed v in a circular orbit of radius r. If the orbit
radius is decreased by 1% its speed will …….
(a) increase by 1%
(b) increase by 0.5%
(c) decrease by 1%
(d) decrease by 0.5%
Answer:
(b) increase by 0.5%

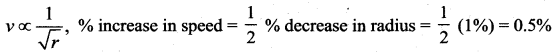
Question 30.
Orbital velocity of an artificial satellite does not depend upon …….
(a) mass of Earth
(b) mass of satellite
(c) radius of Earth
(d) acceleration due to gravity
Answer:
(b) mass of satellite

Question 31.
The orbital speed of Jupiter is …….
(a) greater than the orbital speed of Earth
(b) less then the orbital speed of Earth
(c) zero
(d) equal to the orbital speed of Earth
Answer:
(b) less then the orbital speed of Earth
Hint:

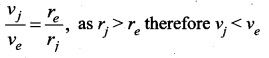
Question 32.
As we go grom the equator to the poles, the value of g …..
(a) remains constant
(b) decreases
(c) increases
(d) decreases upto latitude of 45°
Answer:
(c) increases

Question 33.
The value of g on the Earth surface is 980 cm/sec². Its value at a height of 64 km from the Earth surface is ……. cms²
(a) 960.40
(b) 984.90
(c) 982.45
(d) 977.55
Answer:
(a) 960.40
Hint:

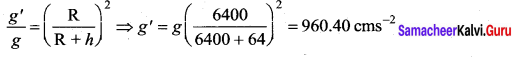
Question 34.
The Moon s radius is \(\frac{1}{4}\) that of earth and its mass is \(\frac{1}{80}\) times that of the Earth. If g represents the acceleration due to gravity on the surface of Earth, that on the surface of the Moon is ……

Answer:
(b) \(\frac{g}{5}\)
Hint:

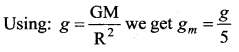
Question 35.
If the density of small planet is that of the same as that of the earth while the radius of the
planet is 0.2 times that of the Earth, the gravitational acceleration on the surface for the planet is ……
(a) 0.2g
(b) 0.4g
(c) 2g
(d) 4g
Answer:
(a) 0.2g
Hint:

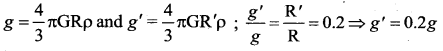
Question 36.
Assuming Earth to be a sphere of a uniform density, what is value of gravitational acceleration in mine 100 km below the Earth surface = ….. ms^-2
(a) 9.66
(b) 7.64
(c) 5.00
(d) 3.1
Answer:
(a) 9.66
Hint:

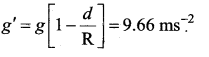
Question 37.
The radii of two planets are respectively R₁ and R₂ and their densities are respectively ρ₁ and ρ₂ the ratio of the accelerations due to gravity at their surface is ……

Answer:
(d) \(g_{1}: g_{2}=\mathrm{R}_{1} \rho_{1}: \mathrm{R}_{2} \rho_{2}\)

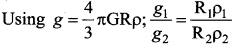
Question 38.
The acceleration due to gravity near the surface of a planet of radius R and density d is proportional to:

Answer:
(c) dR
Hint:

Question 39.
The acceleration of a body due to the attraction of the Earth (radius R) at a distance 2R from the surface of the Earth is …….

Answer:
\(\frac{g}{9}\)
Hint:

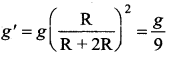
Question 40.
If density of Earth increased 4 times and its radius becomes half of then out weight will be ……
(a) four times its present value
(b) doubled
(c) remains same
(d) halved
Answer:
(b) doubled
Hint:
g ∝ ρR

Question 41.
The radius of the Earth is 6400 km and g = 10 ms^-2 in order that a body of 5 kg weights zero at the equator, the angular speed of the Earth is ….. rad s^-1

Answer:
(c) \(\frac{1}{800}\)
Hint:

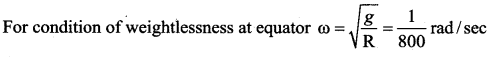
Question 42.
Weight of a body is maximum at …..
(a) Moon
(b) poles of Earth
(c) equator of Earth
(d) centre of Earth
Answer:
(b) poles of Earth

Question 43.
The weight of an astronaut, in an artificial satellite revolving around the Earth is:
(a) zero
(b) equal to that on the Earth
(c) more than that on Earth
(d) less than that on Earth
Answer:
(a) zero

Samacheer Kalvi 11th Physics Gravitation 2 Marks Questions

Question 1.
Distinguish between the terms gravitation and gravity.
Answer:
Gravitation: It is the force of attraction between any two bodies in the universe.
Gravity: It is the force of attraction between the earth and any object lying on or near its surface.

Question 2.
Why is G called the universal gravitational constant?
Answer:
The value of G does not depend on the nature and size of the bodies. It also does not depend on the nature of the medium between the two bodies. That is why G is called universal gravitational constant.

Question 3.
What is meant by the term free fall?
Answer:
The motion of a body under the influence of gravity alone is called a free fall.

Question 4.
What is meant by acceleration due to gravity? Is is a scalar or a vector?
Answer:
The acceleration produced in a freely falling body under the gravitational pull of the earth. It is a vector having direction towards the centre of the earth.

Question 5.
What do you mean by weight of a body? Is it a scalar or vector?
Answer:
Weight of a body is defined as the gravitational force with which a body is attracted towards the centre of the earth. Hence the weight of a body is given by w = mg (or) \(\overrightarrow{\mathrm{W}}=m \vec{g}\)

Question 6.
Define orbital velocity.
Answer:
Orbital velocity is the velocity required to put the satellite into its orbit around the earth.

Question 7.
Give some uses of geostationary satellites.
Answer:

• In communicating radio, T.V and telephone signals across the world.
• In studying upper regions of the atmosphere.
• In forecasting weather.
• In deter ming the exact shape and dimensions of the earth.
• In studying solar radiations and cosmic rays.

Question 8.
Give the uses of polar satellites.
Answer:

• Polar satellites are uses in weather and environment monitoring.
• They are used in spying work for military purposes.
• They are used to study topography of Moon, Venus and Mars.

Samacheer Kalvi 11th Physics Gravitation Numerical Problems

Question 1.
A geo-stationary satellite is orbiting the Earth of a height of 6R above the surface of Earth R being the radius of the Earth calculate the time period of another satellite at a height of 2.5R from the surface of Earth.
Distance of satellite from the center are 7R and 3.5 R respectively.
Answer:

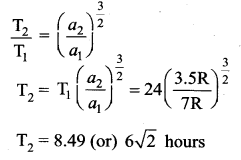
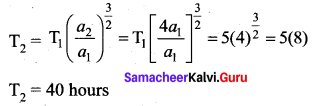
Question 2.
The time period of a satellite of Earth is 5 hours. If the separation between the Earth and the satellite is increased to four times the previous value, the new time period will become.
Answer:

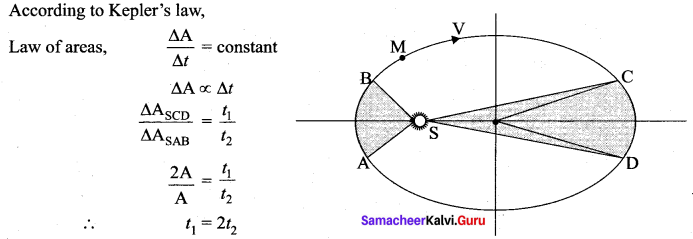
Question 3.
The figure shows elliptical orbit of a planet ‘M’ about the Sun ‘S’, the shaded area SCD is twice the shaded area SAB. If t₁ is the time for the planet to move from C and D and t₂ is the time to move from A to B then.
Answer:

Question 4.
A satellite moves in a circle around the Earth, the radius of this circle is equal to one half of the radius of the Moon’s orbit. The satellite completes one revolution in…… lunar month.
Answer:
Time period of revolution of moon around the Earth T_m = 1 lunar month

Question 5.
Two identical solid copper spheres of radius R are placed in contact with each other. The gravitational force between them is proportional to.
Answer:


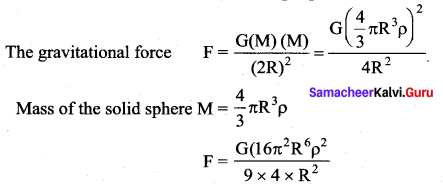
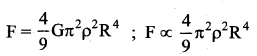
∴ The gravitational force between them is proportional to 4th power of radius.

Question 6.
Two satellites A and B of the same mass are revolving around the Earth in circular orbits such that the distance of B from the centre of the Earth is thrice as compared to the distance of A from the centre. What will be the ratio of centripetal force on B to that on A.
Answer:
The necessary centripetal force is provided by the gravitational force of attraction, for circular orbit

The ratio of centripetal force,

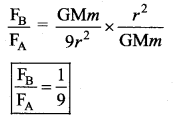
Question 7.
An infinite number of bodies, each of mass 2 kg, are situated on x-axis at distances lm, 2m, 4m, 8m from the origin. What will be the resultant gravitational potential due to this system at the origin.
Answer:
Gravitational potential at the origin is

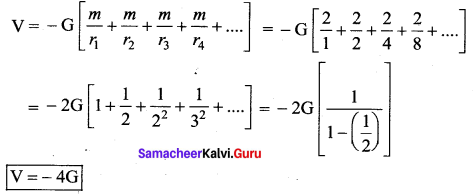
Question 8.
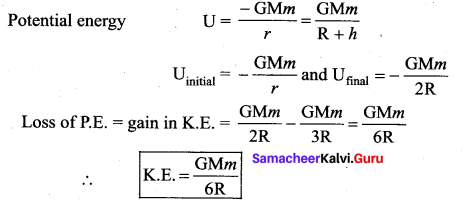
A body of mass ‘m’ kg starts falling from a point 2R above the Earth’s surface. What is its K.E. When it has fallen to a point ‘R’ above the Earth’s surface.
Answer:

Question 9.
A particle of mass 10g is kept on the surface of a uniform sphere of mass 100 kg and radius 10 cm. Find the work to done against the gravitational force between them to take the particle is away from the sphere.
Answer:

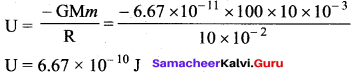
So, the amount of work done to take the particle upto infinite will be 6.67 × 10^-10 J

Question 10.
The mass of a space ship is 1000 kg. It is to be launched from Earth ’s surface out into free space the value of g and R (radius of Earth) are 10 ms^-2 and 6400 km respectively. The required energy for this work will be.
Answer:
Potential energy U = – mgR_e + mgh
(The first term is independent of the height, so it can be taken to zero.)
W = U = mgh [h ≈ R]
= 1000 × 10 × 6400 × 10³ = 64 × 10⁹
W = 6.4 × 10¹⁰ J

Question 11.
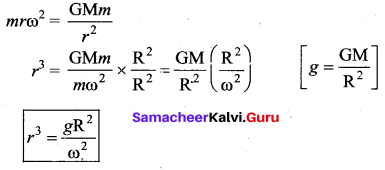
If the mean radius of the Earth is R, its angular velocity is ω, and the acceleration due to gravity at the surface of the Earth is g, then what will be the cube of the radius of the orbit of a geostationary satellite.
Answer:
Let r be the radius of the geostationary orbit. Angular velocity of revolution of a geostationary satellite is same as the angular velocity of rotation of the Earth.

Question 12.
The escape velocity of a body from Earth’s surface is v_e. What will be the escape velocity of the same body from a height equal to 7R from Earth’s surface.
Answer:

Question 13.
If R is the radius of the Earth and g is the acceleration due to gravity on the Earth’s surface. Find the mean density of the Earth.
Acceleration due to gravity g = \(\frac{\mathrm{GM}}{\mathrm{R}^{2}}\)

Question 14.
If the mass of Earth is 80 times of that of a planet and diameter is double that of planet and ‘g’ on the Earth is 9.8 ms-2. Calculate the value of ‘g’ on that planet?
Answer:

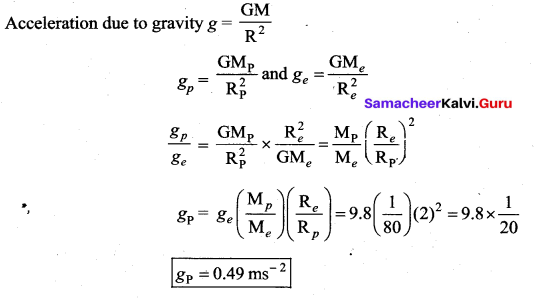
Question 15.
At what distance from the centre of Earth, the value acceleration due to gravity ‘g’ will be half that of the surface?
Answer:
According to acceleration due to gravity

Question 16.
A body weight 700 g on the surface of Earth. How much it weight on the surface of planet whose mass is \(\frac{1}{7}\) and radius is half that of the Earth.
Answer:
Acceleration due to gravity g = \(\frac{\mathrm{GM}}{\mathrm{R}^{2}}\)

Question 17.
An object weight 72 N on the Earth. What its weight at a height \(\frac{\mathbf{R}}{2}\) from Earth.
Answer:

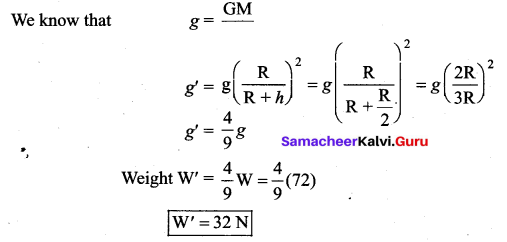
Question 18.
A body weight 500 N on the surface of the Earth. How much would it weight half way below the surface of Earth.
Answer:
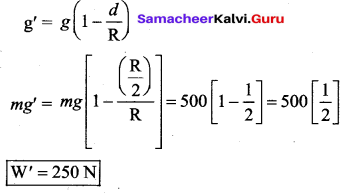
Weight on surface of Earth, mg = 500 N
Weight below the surface of Earth at d = \(\frac{\mathrm{R}}{2}\)
From variation of ‘g’ with depth