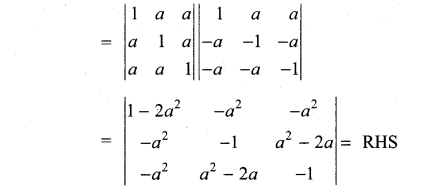You can Download Samacheer Kalvi 11th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 7 Matrices and Determinants Ex 7.4
Question 1.
Find the area of the triangle whose vertices are (0, 0), (1, 2) and (4, 3)
Solution:
Area of triangle with vertices
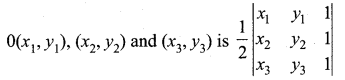
∴ Area of A with vertices (0, 0), (1, 2) and (4, 3) is

![]()
(as the area cannot be negative).
Question 2.
If (k, 2), (2, 4) and (3, 2) are vertices of the triangle of area 4 square units then determine the value of k.
Solution:

Question 3.
Identify the singular and non-singular matrices:
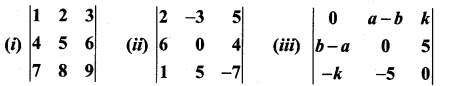
Solution:
(i) For a given square matrix A,
1. If |A| = 0 then it is a singular matrix.
2. If |A| ≠ 0 then it is a non singular matrix.
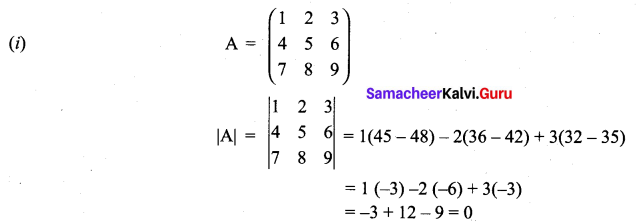
⇒ A is a singular matrix.

Which is a skew symmetric matrix
∴ |A| = 0 ⇒ A is a singular matrix.
![]()
Question 4.
Determine the value of a and b so that the following matrices are singular:
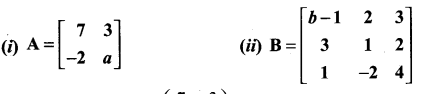
Solution:
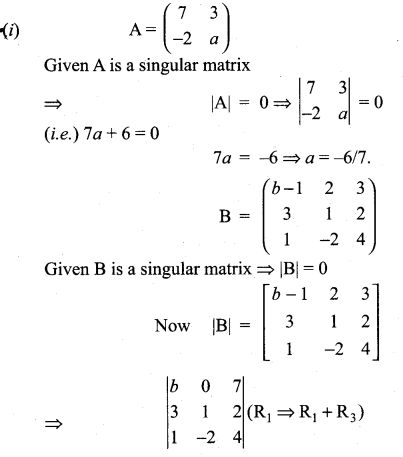
expanding along R1
b(4 + 4) + 7 (-6 – 1) = 0 (given)
8b + 7 (-7) = 0
(i.e.,) 8b – 49 = 0 ⇒ 8b = 49 ⇒ b = 49/8
Question 5.
If cos 2θ = 0, determine \(\left[\begin{array}{ccc}{\theta} & {\cos \theta} & {\sin \theta} \\ {\cos \theta} & {\sin \theta} & {0} \\ {\sin \theta} & {0} & {\cos \theta}\end{array}\right]^{2}\)
Solution:

Question 6.
Find the value of the product; 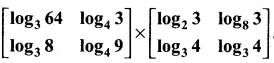
Sol:

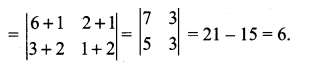
Samacheer Kalvi 11th Maths Solutions Chapter 7 Matrices and Determinants Ex 7.4 Additional Problems
Question 1.
Identify the singular and non-singular matrix.
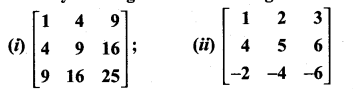
Solution:
If the determinant value of a square matrix is zero it is called a singular matrix. Otherwise it is non-singular.
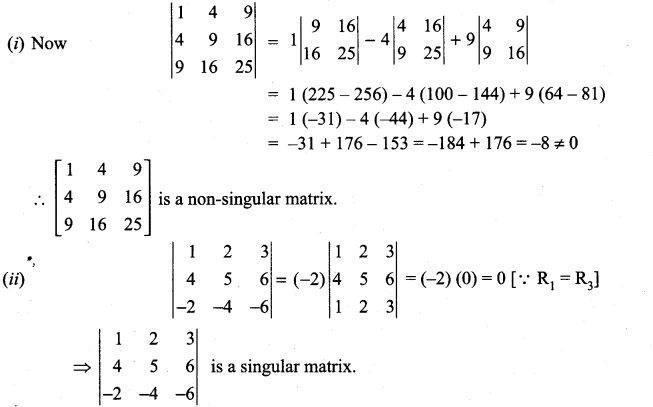
![]()
Question 2.
Show that 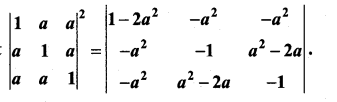
Solution: