Samacheer Kalvi 11th Maths Solutions Chapter 5 Binomial Theorem, Sequences and Series Ex 5.1

You can Download Samacheer Kalvi 11th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 5 Binomial Theorem, Sequences and Series Ex 5.1

Question 1.

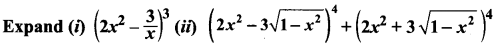
Solution:


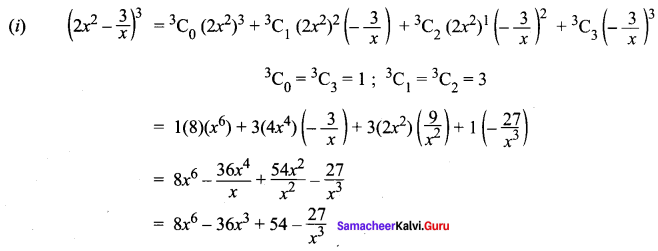
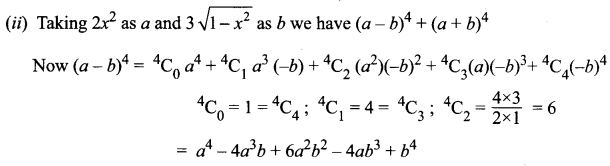
Similarly (a + b)⁴ = a⁴ + 4a³b + 6a²b² + 4ab³ + b⁴
∴ (a – b)⁴ + (a + b)⁴ = 2 [a⁴ + 6a²b² + b⁴]
Substituting the value of a and b we get

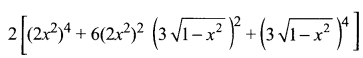
= 2[16x⁸ + 6(4x⁴)(9(1 – x²)) + 81(1 – x²)²]
= 2[16x⁸ + 216x⁴(1 – x²) + 81(1 – x²)²]
= 2[16x⁸ + 216x⁴ – 216x⁶ + 81 + 81x⁴ – 162x²]
= 2[16x⁸ – 216x⁶ + 297x⁴ – 162x² + 81]
= 32x⁸ – 432x⁶ + 594x⁴ – 324x² + 162

Question 2.
Compute
(i) 102⁴
(ii) 99⁴
(iii) 9⁷
Solution:

(i) 102⁴ = (100 + 2)⁴ = (10² + 2)⁴

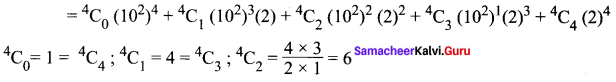
= 1(10⁸) + 4(10⁶)(2) + 6(10⁴)(4) + 4(10²)(8) + 16
= 100000000 + 8000000 + 240000 + 3200 + 16
= 108243216

(ii) 994 = (100 – 1)⁴ = (10² – 1)⁴

= 1(10⁸) + 4(10⁶)(-1) + 6 (10⁴)(1) + 4( 10⁴)(-1) + (-1)⁴
= 100000000 – 4000000 + 60000 – 400 + 1
= 100060001 – 4000400 = 96059601

(iii) 9⁷ = (10 – 1)⁷

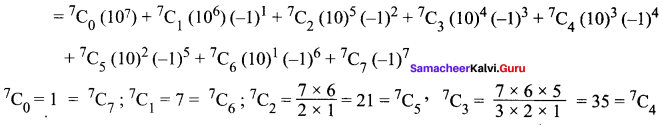
= 1(10000000) + 7(1000000)(-1) + 21(100000)(1) + 35(10000)(-1) + 35(1000)(1) + 21(100)(-1) + 7(10)(1) + 1(-1)
= 10000000 – 7000000 + 2100000 – 350000 + 35000 – 2100 + 70 – 1
= 12135070 – 7352101 = 4782969

Question 3.
Using binomial theorem, indicate which of the following two number is larger: (1.01)^1000000, 10000.
Solution:
(1.01)^1000000 = (1 + 0.01)^1000000

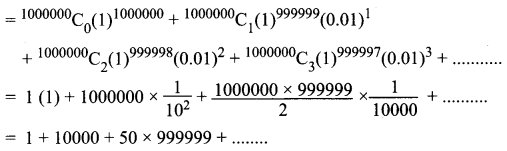
which is > 10000
So (1.01)^1000000 > 10000 (i.e.) (1.01)^1000000 is larger

Question 4.

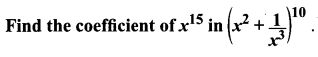
Solution:

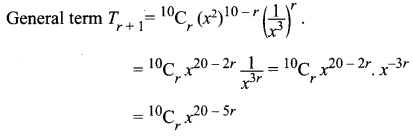
To find a coefficient of x¹⁵ we have to equate x power to 15
i.e. 20 – 5r = 15
20 – 15 = 5r ⇒ 5r = 5 ⇒ r = 5/5 = 1
So the coefficient of x¹⁵ is ¹⁰C₁ = 10

Question 5.

Solution:

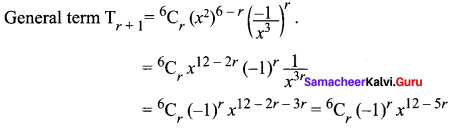
To find coefficient of x⁶
12 – 5r = 6
12 – 6 = 5r ⇒ 5r = 6 ⇒ r = 6/5 which is not an integer.
∴ There is no term involving x⁶.
To find coefficient of x²
12 – 5r = 2
5r = 12 – 2 = 10 ⇒ r = 2

Question 6.

Solution:

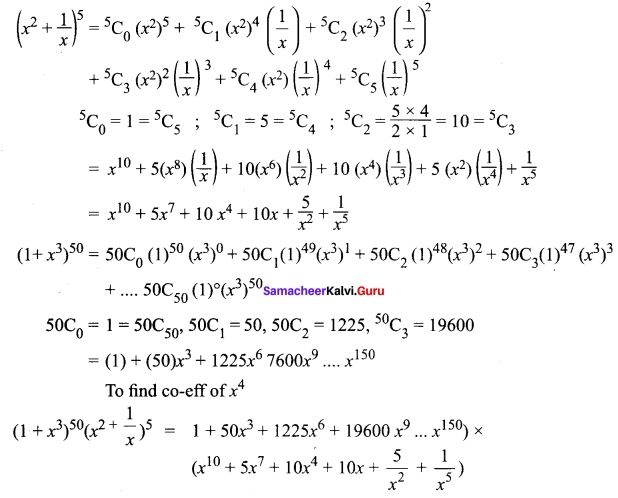
when multiplying these terms, we get x⁴ terms

∴ The co-eff of x⁴ is 26325

Question 7.

Solution:

Question 8.
Find the last two digits of the number 3⁶⁰⁰.
Solution:
3⁶⁰⁰ = 3^{2 × 300} = (9)300 = (10 – 1)³⁰⁰

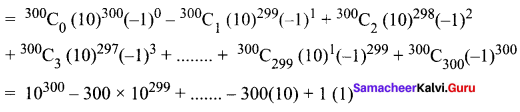
All the terms except last term are ÷ by 100. So the last two digits will be 01.

Question 9.
If n is a positive integer, show that, 9^{n + 1} – 8n – 9 is always divisible by 64.
Solution:

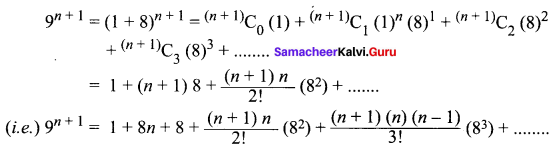
∴ 9^{n + 1} – 8n – 9 = 64 [an integer]
⇒ 9^{n + 1} – 8n – 9 is divisible by 64

Question 10.
If n is an odd positive integer, prove that the coefficients of the middle terms in the expansion of (x + y)ⁿ are equal.
Solution:
Given n is odd. So let n = 2n + 1, where n is an integer.
The expansion (x + y)ⁿ has n + 1 terms.
= 2n + 1 + 1 = 2(n + 1) terms which is an even number.

⇒ The coefficient of the middle terms in (x + y)ⁿ are equal.

Question 11.
If n is a positive integer and r is a non – negative integer, prove that the coefficients of x^r and x^{n – r} in the expansion of (1 + x)ⁿ are equal.
Solution:

Question 12.
If a and b are distinct Integers, prove that a – b is a factor of aⁿ – bⁿ, whenever n is a positive integer. [Hint: write aⁿ = (a – b + b)ⁿ and expand]
Solution:

= (a – b)[aⁿ integer]
⇒ aⁿ – bⁿ is divisible by (a – b)

Question 13.
In the binomial expansion of (a + b)aⁿ, the coefficients of the 4^th and 13^th terms are equal to each other, find n.
Solution:
In the expansion of (a + b)ⁿ,
The general term is T_r+1 = nC_r . a^n-r . b^r ……….. (1)
To find the coefficient of 4th term, Put r = 3 in equation (1)
∴ T₃₊₁ = nC₃ a^n-3 . b³
To find the coefficient of 13th term , Put r = 12 in equation (1)
∴ T₁₂₊₁ = nC₁₂ a^n-12 . b¹²
Given nC₃ = nC₁₂
nC_x = nC_y ⇒ x = y or x + y = n
∴ 3 + 12 = n ⇒ n = 15

Question 14.
If the binomial coefficients of three consecutive terms in the expansion of (a + x)ⁿ are in the ratio 1 : 7 : 42, then find n.
Solution:
In (a + x)ⁿ general term is t_{r + 1} = ⁿC_r
So, the coefficient of t_{r + 1} is ⁿC_r
We are given that the coefficients of three consecutive terms are in the ratio 1 : 7 : 42.

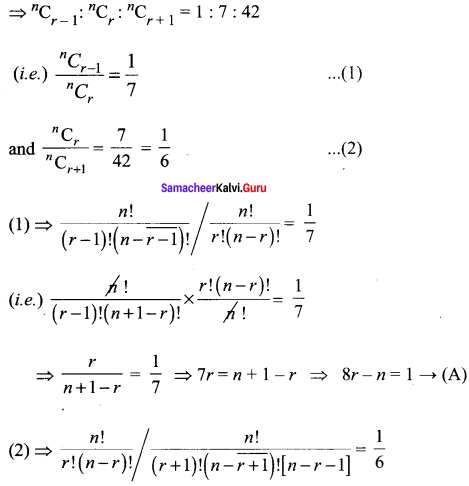
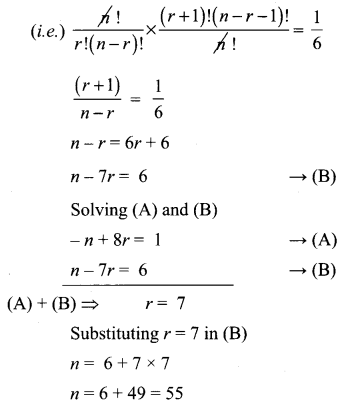
Question 15.
In the binomial coefficients of (1 + x)ⁿ, the coefficients of the 5^th, 6^th and 7 terms are in AP. Find all values of n.
Solution:

⇒ (n – 1)(n – 14) = 0
∴ n = 7 , 14

Question 16.

Solution:

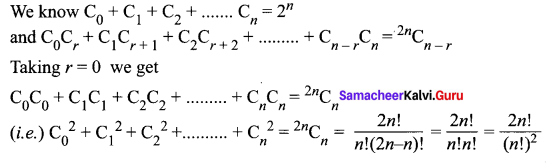
Samacheer Kalvi 11th Maths Solutions Chapter 5 Binomial Theorem, Sequences and Series Ex 5.1 Additional Questions Solved

Question 1.

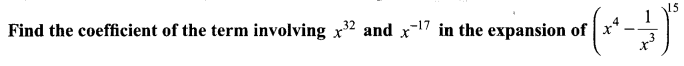
Solution:
Let T_{r + 1} be the term in which x³² and x^-17 occurs,

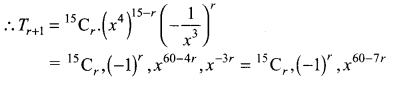
(i) Since x³² occurs in this term
∴ Exponent of x = 32
⇒ 60 – 7r = 32 ⇒ 7r = 28
r = 28 ÷ 7 = 4
∴ Coefficient of the term containing x³² = ¹⁵C₄ (-1)⁴ = 1365

(ii) Since x^-17 occurs in this term .
∴ Exponent of x = -17
⇒ 60 – 7r = -17 ⇒ 7r = 77, ∴ r = 11

Question 2.
Find a positive value of m for which the coefficient of x² in the expansion of (1 + x)^m is 6.
Solution:

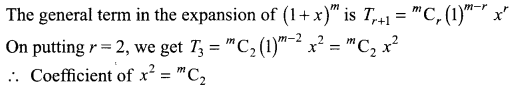
Also, coefficient of x² in the expansion of (1 + x)^m is 6

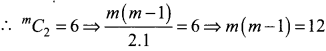
⇒ m (m – 1) = 4.3 ⇒ m = 4

Question 3.
In the binomial expansion of (1 + a)^{m + n}, prove that the coefficients of a^m and aⁿ are equal.
Solution:

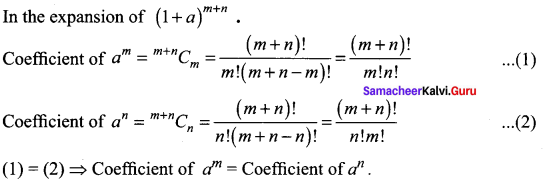
Question 14.
The coefficient of (r – 1)^th, r^th, and (r + 1)^th terms in the expansion of (x + 1)ⁿ are in the ratio 1 : 3 : 5. Find both n and r.
Solution:
We know that co-effcients of (r – 1)^th, r^th and (r + 1)^th terms in the expansion of (x + 1)ⁿ are ⁿC_{r – 2}: ⁿC_{r – 1} and ⁿC_r respectively

⇒ 3n – 8r + 3 = 0 and n – 4r + 5 = 0
Solving these for n, r we get,
n = 7 and r = 3

Question 5.

Solution:

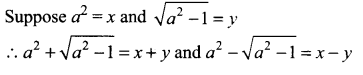
Using the binomial theorem,

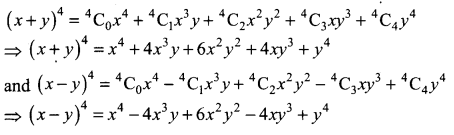
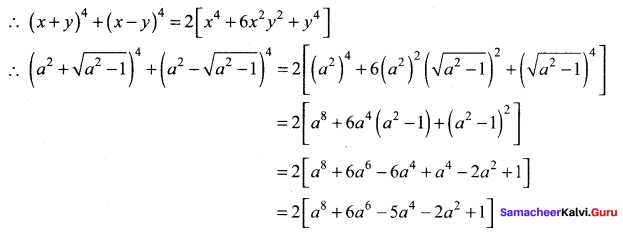
Question 6.
Show that the coefficient of the middle term in the expansion of (1 + x)²ⁿ is equal to the sum of the coefficients of the two middle terms in the expansion of (1 + x)^{2n – 1}.
Solution:
In the expansion of (1 + x)²ⁿ,
Number of terms = 2n + 1, which is odd

Question 7.
If three consecutive coefficients in the expansion of (1 + x)ⁿ are in the ratio 6 : 33 : 110, find n.
Solution:
Let the consecutive coefficients ⁿC_r, ⁿC_{r + 1} and ⁿC_{r + 2} be the coefficients of T_{r + 1}, T_{r + 2} and T_{r + 3} then ⁿC_r : ⁿC_{r + 1} : ⁿC_{r + 2} = 6 : 33 : 110

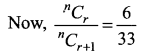
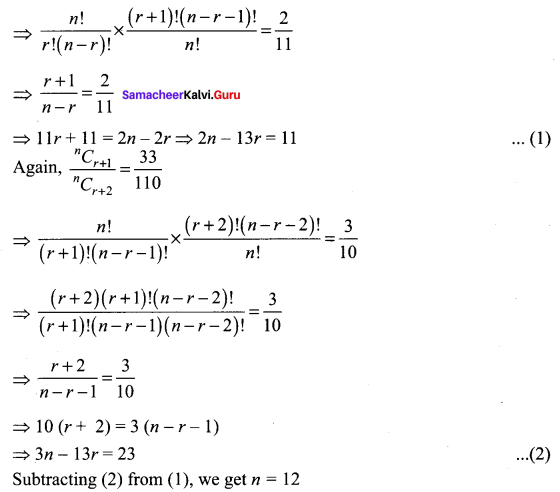
Question 8.
If the sum of the coefficients in the expansion of (x + y)ⁿ is 4096. Then find the greatest coefficient in the expansion.
Solution:
Given that, Sum of the coefficients in the expansion of (x + y)ⁿ = 4096
∴ ⁿC₀ + ⁿC₁ + ⁿC₂+…+ ⁿC_n = 4096
[∴ Sum of binomial coefficients in the expansion of (x + a)ⁿ is 2ⁿ]
⇒ 2ⁿ = 4096 = 2¹²

Question 9.

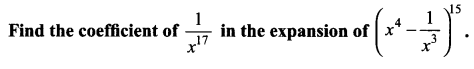
Solution:
The general term in the expansion of

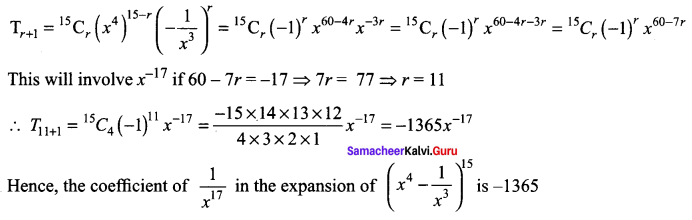
Question 10.

Solution: