You can Download Samacheer Kalvi 11th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 3 Trigonometry Ex 3.5
Question 1.
Find the value of cos 2A, A lies in the first quadrant, when
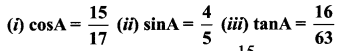
Solution:
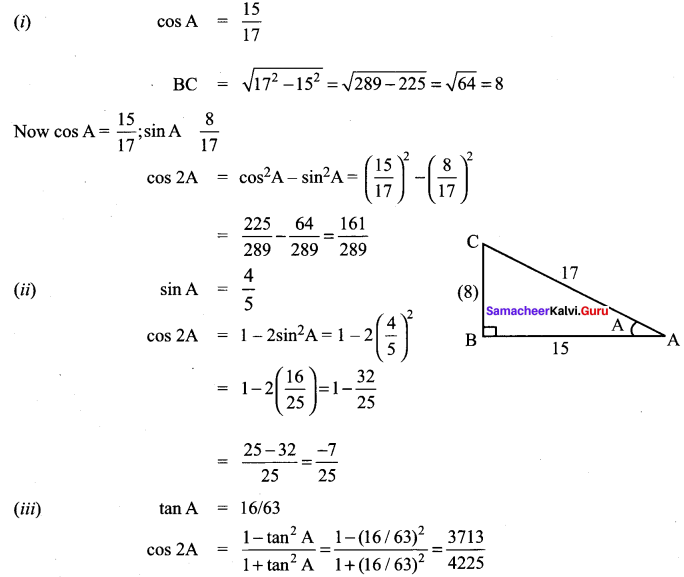
Question 2.
If θ is an acute angle, then find
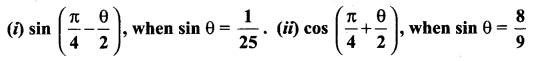
Solution:
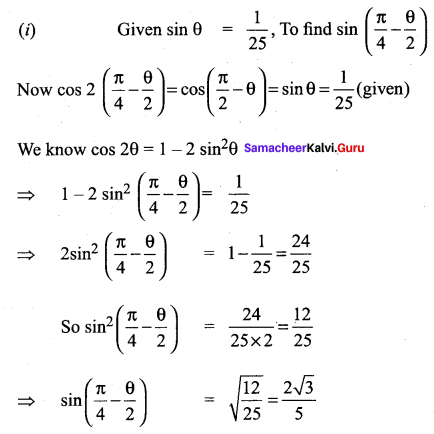
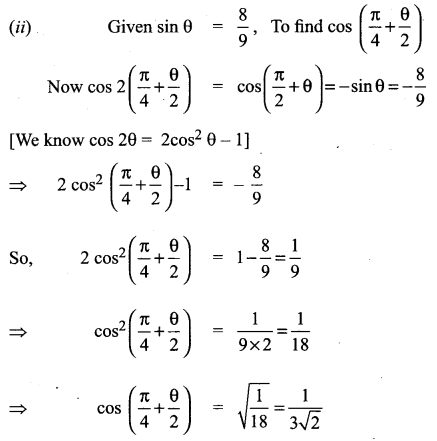
![]()
Question 3.

Solution:

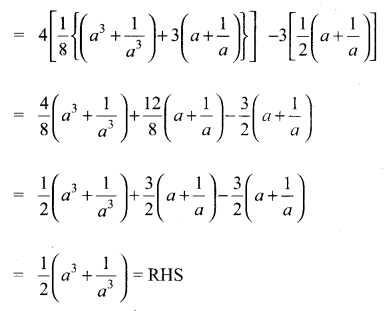
Question 4.
Prove that cos 5 θ = 16 cos5 θ – 20 cos3 θ + 5 cos θ.
Solution:
cos 5 θ = cos(2θ + 3θ) = cos 2θ cos 3θ – sin 2θ sin 3θ
= (2 cos2 θ – 1) (4 cos3 θ – 3 cos θ) – 2 sin θ cos θ (3 sin θ – 4 sin3 θ)
= 8cos5 θ – 6 cos3 θ – 4 cos3 θ + 3 cos θ – 6 sin2 θ cos θ + 8 cos θ sin4 θ
= 8 cos5 θ – 6 cos3 θ – 4 cos3 θ + 3 cos θ – 6(1 – cos2 θ) cos θ + 8 cos θ (1 – cos2 θ)2
= 8 cos5 θ – 6 cos3 θ – 4 cos3 θ + 3 cos θ – 6 cos θ + 6 cos3 θ + 8 cos 0(1+ cos4 θ – 2 cos2 θ)
= 8 cos5 θ – 6 cos3 θ – 4 cos3 θ + 3 cos θ – 6 cos θ + 6 cos3 θ + 8 cos θ + 8 cos5 θ – 16 cos3 θ
= 16 cos5 θ – 20 cos3 θ + 5 cos θ = RHS
Question 5.
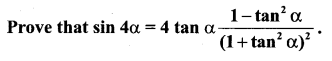
Solution:
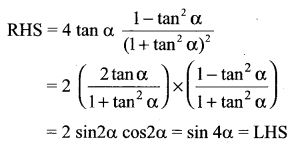
Question 6.
If A + B = 45°, show that (1 + tanA) (1 + tanB) = 2.
Solution:
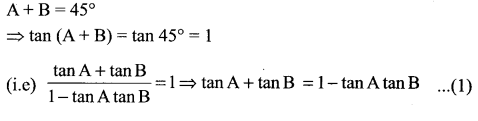
Now LHS = (1 + tan A) (1 + tan B)
= tan A + tan B + tan A tan B + 1
= (1 – tan A tan B) + (tan A tan B + 1) from (1)
= 2 = RHS
Question 7.
Prove that (1 + tan 1°)(1 + tan 2°)(1 + tan 3°)… (1 + tan 44°) is a multiple of 4.
Solution:
Let T = (1 + tan 1°) ( 1 + tan 2°) (1 + tan 3°) ………. (1 + tan44°)
T = (1 + tan 1°) (1 + tan 44°) (1 + tan 2°) (1 + tan 43°) (1 + tan 3°) (1 + tan 42°) ………. (1 + tan 22°) (1 + tan 23°)
[If A + B = 45°,then (1 + tan A) (1 + tan B) = 2]
= 2 × 2 × 2 × …………………. 22 times
T = 222 = (22)11 = 411 which is a multiple of 4.
Therefore, (1 + tan 1°) (1 + tan 2°) (1 + tan 3°) ………….. (1 + tan 44°) is a multiple of 4
Question 8.
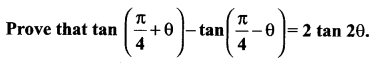
Solution:

Question 9.
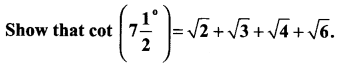
Solution:
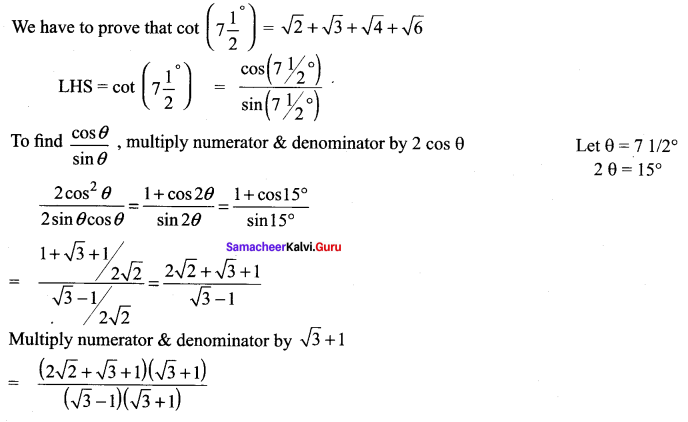
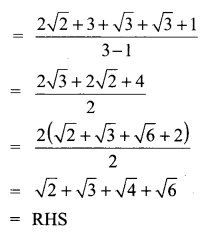
![]()
Question 10.
Prove that (1 + sec 2θ)(1 + sec 4θ)….. (1 + sec 2nθ) = tan 2nθ
Solution:

Question 11.
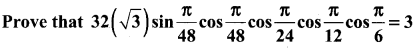
Solution:
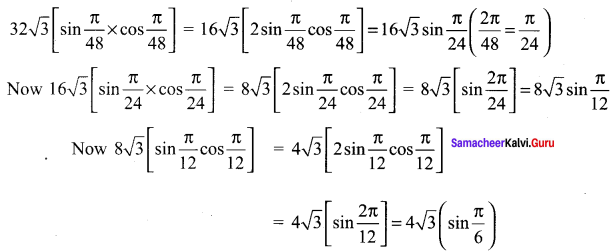
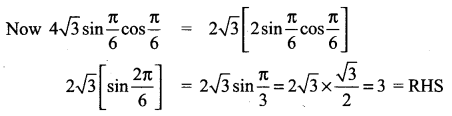
Samacheer Kalvi 11th Maths Solutions Chapter 3 Trigonometry Ex 3.5 Additional Questions
Question 1.
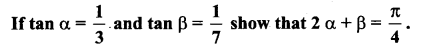
Solution:

Question 2.

Solution:
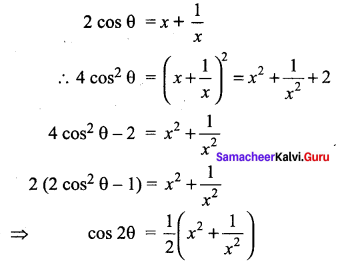
![]()
Question 3.
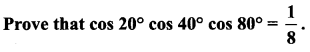
Solution:
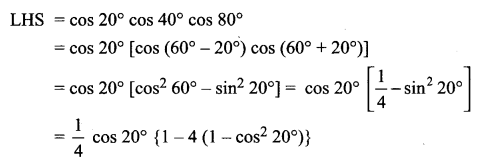

Question 4.
Show that 4 sin A sin (60° + A). sin(60° – A) = sin 3A
Solution:
LHS = 4sinAsin(60° + A). sin(60° – A)
= 4 sin A{sin (60° + A). sin (60° – A)}
= 4 sin A {sin2 60° – sin2 A)}