You can Download Samacheer Kalvi 11th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 12 Introduction to Probability Theory Ex 12.4
Question 1.
A factory has two Machines-I and II. Machine-I produces 60% of items and Machine-II produces 40% of the items of the total output. Further, 2% of the items produced by Machine-I are defective whereas 4% produced by Machine-II are defective. If an item is drawn at random what is the probability that it is defective?
Solution:

![]()
Question 2.
There are two identical urns containing respectively 6 black and 4 red balls, 2 black and 2 red balls. An urn is chosen at random and a ball is drawn from it, (z) find the probability that the ball is black (ii) if the ball is black, what is the probability that it is from the first urn?
Solution:

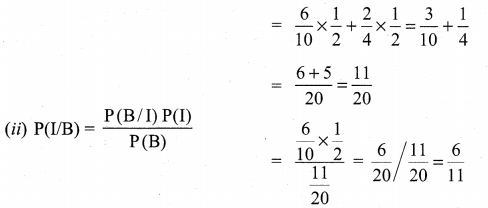
Question 3.
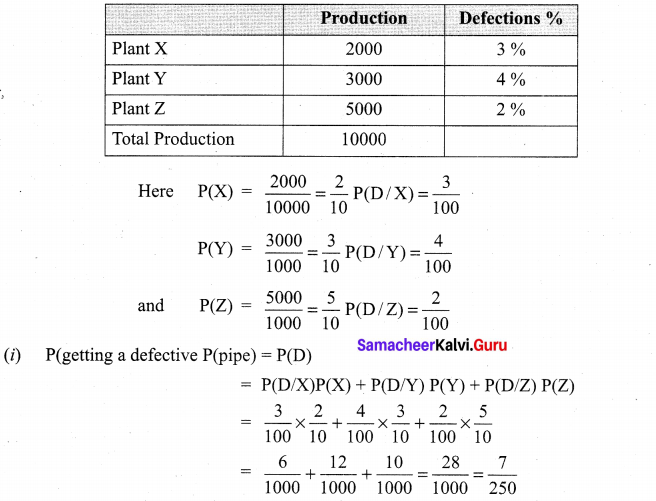
A firm manufactures PVC pipes in three plants viz, X, Y and Z. The daily production volumes from the three firms X, Y and Z are respectively 2000 units, 3000 units and 5000 units. It is known from the past experience that 3% of the output from plant X, 4% from plant Y and 2% from plant Z are defective. A pipe is selected at random from a day’s total production,
(i) find the probability that the selected pipe is a defective one.
(ii) if the selected pipe is a defective, then what is the probability that it was produced by plant Y?
Solution:
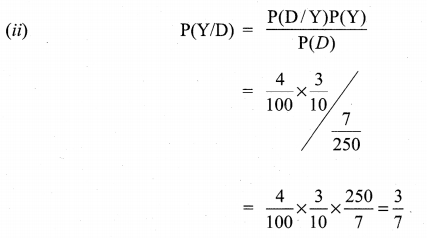
Question 4.
The changes of A, B, and C becoming manager of a certain company are 5 : 3 : 2. The probabilities that the office canteen will be improved if A, B, and C become managers are 0.4, 0.5 and 0.3 respectively. If the office canteen has been improved, what is the probability that B was appointed as the manager?
Solution:
Given A : B : C = 5 : 3 : 2

![]()
Question 5.
An advertising executive is studying television viewing habits of married men and women during prime time hours. Based on the past viewing records he has determined that during prime time wives are watching television 60% of the time. It has also been determined that when the wife is watching television, 40% of the time the husband is also watching. When the wife is not watching the television, 30% of the time husband is watching the television. Find the probability that (i) the husband is watching the television during the prime time of television (ii) if the husband is watching the television, the wife is also watching the television.
Solution:
Let A be the event of wife watching the TV
B1 be the event of the husband watching the TV when the wife watching.
Probability of wife watching the TV = \(\frac{60}{100}\) = 0.6
Probability of husband watching the TV = \(\frac{40}{100}\) = 0.4
Let B2 be the event of the husband watching the TV when the wife not watching TV.
P(B2) = \(\frac{30}{100}\) = 0.3
P(A̅) = 1 – P(A)
= 1 – 0.6 = 0.4
(i) the husband is watching the television during the prime time of television:
Probability husband watching TV = Probability of wife watching the TV and husband watching the TV or wife not watching TV and husband watching the TV
= P[(A ∩ B1) ∪ (A̅ ∩ B2)]
= P[(A ∩ B1) + (A̅ ∩ B2)]
= 0.6 × 0.4 + 0.4 × 0.3
= 0.24 + 0.12 = 0.36
= \(\frac{36}{100}\) = \(\frac{9}{25}\)
Samacheer Kalvi 11th Maths Solutions Chapter 12 Introduction to Probability Theory Ex 12.4 Additional Problems
Question 1.
A factory has two Machines-I and II. Machines-I produces 25% of items and Machine-II produces 75% of the items of the total output. Further, 3% of the items produced by Machine-I are defective whereas 4% produced by Machine-II are defective. If an item is drawn at random what is the probability that it is defective?
Solution:
Let A1 be the event that the items are produced by Machine-I and A2 be the event that the items are produced by Machine-II.
Let B the event of drawing a defective item

Question 2.
There are two identical boxes containing respectively 5 white and 3 red balls, 4 white and 6 rpd balls. A box is chosen at random and a ball is drawn from it
(i) find the probability that the ball is white
(ii) if the ball is white, what is the probability that it from the first box?
Solution:
Let A1 be the event of selecting the first box and A2 be the event of selecting the second box.
Let B be the event of selecting a white ball.
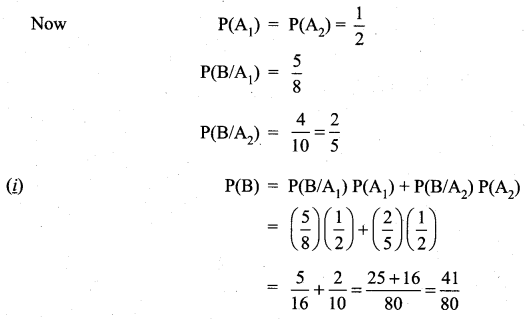
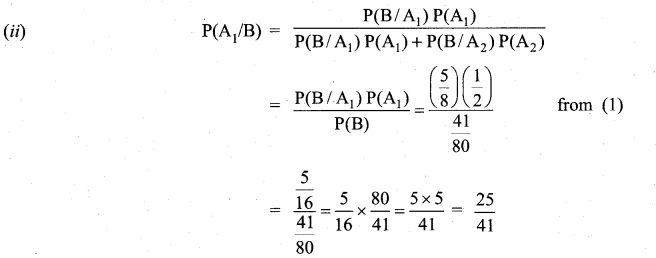
![]()
Question 3.
In a factory, Machine-I produces 45% of the output and Machine-II produces 55% of the output. On average 10% of items produced by Machine-I and 5% of the items produced by II are defective. An item is drawn at random from a day’s output, (i) Find the probability that it is a defective item
(ii) If it is defective, what is the probability that it was produced by Machine-II?
Solution:
Let A1 and A2 be the events that the items produced by Machine-I and II respectively.
Let B be the event of selecting a defective item
