Samacheer Kalvi 11th Maths Solutions Chapter 2 Basic Algebra Ex 2.13

You can Download Samacheer Kalvi 11th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 2 Basic Algebra Ex 2.13

Choose the correct or the most suitable questions.

Question 1.
If |x + 2| ≤ 9, then x belongs to
(a) (-∞, -7)
(b) [-11, 7]
(c) (-∞, -7) ∪ [11, ∞)
(d)(-11, 7)
Solution:
(b) [-11, 7]
Hint:
Given |x + 2| ≤ 9
– 9 ≤ (x + 2) ≤ 9
– 9 – 2 ≤ x ≤ 9 – 2
– 11 ≤ x ≤ 7
∴ x ∈ [-11, 7]

Question 2.
Given that x, y and b are real numbers x < y, b ≥ 0, then ……..
(a) xb < yb (b) xb > yb
(c) xb ≤ vb
(d) xlb ≥ ylb
Solution:
(a) xb < yb
Hint:

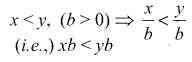
Question 3.

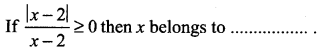
(a) [2, ∞]
(b) (2, ∞)
(c) (-∞, 2)
(d) (-2, ∞)
Solution:
(b) (2, ∞)
Hint:

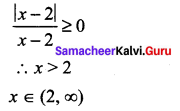
Question 4.
The solution of 5x – 1 < 24 and 5x + 1 > -24 is …….
(a) (4, 5)
(b) (-5, -4)
(c) (-5, 5)
(d) (-5, 4)
Solution:
(c) (-5, 5)
Hint:

Question 5.
The solution set of the following inequality |x – 1| ≥ |x – 3| is …….
(a) [0, 2]
(b) (2, ∞)
(c) (0, 2)
(d) (-∞, 2)
Solution:
(b) (2, ∞)

Question 6.

(a) 16
(b) 18
(c) 9
(d) 12
Solution:
(b) 18
Hint:

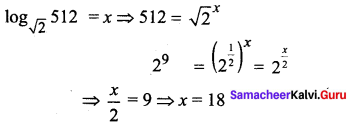
Question 7.

(a) -2
(b) -8
(c) -4
(d) -9
Solution:
(c) -4
Hint:

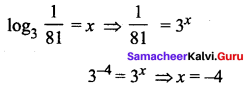
Question 8.

(a) 0.5
(b) 2.5
(c) 1.5
(d) 1.25
Solution:
(a) 0.5
Hint:

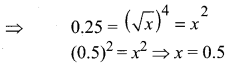
Question 9.

(a) 2
(b) 1
(c) 3
(d) 4
Solution:
(b) 1
Hint:

Question 10.
If 3 is the logarithm of 343, then the base is ……
(a) 5
(b) 7
(c) 6
(d) 9
Solution:
(b) 7
Hint.
Given log_x 343 = 3
343 = x³
7 × 7 × 7 = x³
7³ = x³
x = 7
Base of the logarithm x = 7

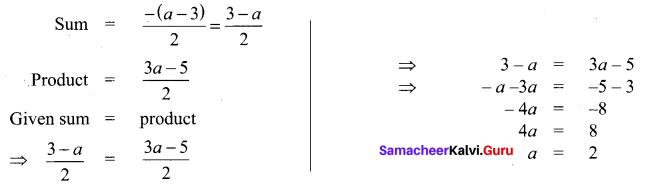
Question 11.
Find a so that the sum and product of the roots of the equation 2x² + (a – 3)x + 3a – 5 = 0 are equal is ……..
(a) 1
(b) 2
(c) 0
(d) 4
Solution:
(b) 2
Hint:

Question 12.
If a and b are the roots of the equation x² – kx + 16 = 0 and satisfy a² + b² = 32, then the value of k is ……
(a) 10
(b) -8
(c) (-8, 8)
(d) 6
Solution:
(c) -8, 8
Hint:
Given a and b are the roots of x² – kx + 16 = 0 satisfying a² + b² = 32
Sum of the roots a + b = \(\frac{-(-k)}{1}\)
a + b = k
Product of the roots ab = \(\frac{16}{1}\)
ab = 16
a² + b² = (a + b)² – 2ab
32 = k² – 2 × 16
32 = k² – 32
k² = 32 + 32 = 64
k = ± 8

Question 13.
The number of solutions of x² + |x – 1| = 1 is ………
(a) 1
(b) 0
(c) 2
(d) 3
Solution:
(c) 2

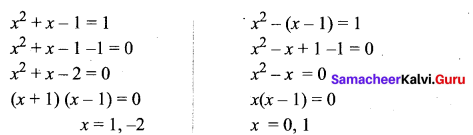
We have two solutions 0, 1

Question 14.
The equations whose roots are numerically equal but opposite in sign to the roots of 3x² – 5x – 7 = 0 is ……
(a) 3x² – 5x – 7 = 0
(b) 3x² + 5x – 7 = 0
(c) 3x² – 5x + 7 = 0
(d) 3x² + x – 7 = 0
Solution:
(b) 3x² + 5x – 7 = 0
Hint:

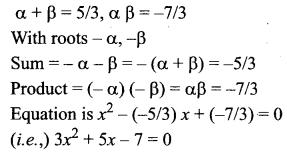
Question 15.
If 8 and 2 are the roots of x² + ax + c = 0 and 3, 3 are the roots of x² + ax + b = 0, then the roots of the equation x² + ax + b = 0 are …….
(a) 1, 2
(b) -1, 1
(c) 9, 1
(d) -1, 2
Solution:
(c) 9, 1
Hint:
Sum = 8 + 2 = 10 = -a ⇒ a = -10
Product = 3 × 3 = 9 = b ⇒ b = 9
Now the equation x² + ax + b = 0
⇒ x² – 10x + 9 = 0
⇒ (x- 9) (x – 1) = 0
x = 1 or 9

Question 16.
If a and b are the real roots of the equation x² – kx + c = 0, then the distance
between the points (a, 0) and (b, 0) is ……..

Solution:

Hint:
a + b = k, ab = c

Question 17.

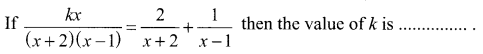
(a) 1
(b) 2
(c) 3
(d) 4
Solution:
(c) 3

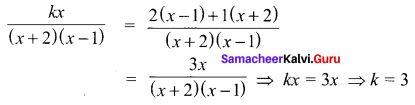
Question 18.

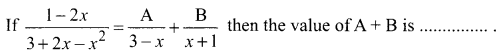
(a) -1/2
(b) -2/3
(c) 1/2
(d) 2/3
Solution:
(a) -1/2
Hint:

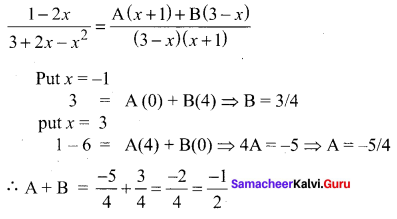
Question 19.
The number of real roots of (x + 3)⁴ + (x + 5)⁴ = 16 is ……
(a) 4
(b) 2
(c) 3
(d) 0
Solution:
(a) 4
Hint:
The given equation is (x + 3)⁴ + (x + 5)⁴ = 16
Since it is a fourth degree equation it has four roots.
∴ Number of roots = 4

Question 20.
The value of log₃ 11 . log₁₁ 13 . log₁₃ 15 . log₁₅ 27 . log₂₇ 81 is …….
(a) 1
(b) 2
(c) 3
(d) 4
Solution:
(d) 4
Solution:
(d) 4
Hint.
log₃ 11 . log₁₁ 13 . log ₁₃ 15 . log ₁₅ 27 . log ₂₇ 81
= log₃ 13 . log ₁₃ 15 . log ₁₅ 27 . log ₂₇ 81
= log ₃ 15 . log ₁₅ 27 . log ₂₇ 81
= log ₃ 27 . log ₂₇ 81
= log ₃ 81
= log ₃3⁴
= 4 log ₃3
= 4 × 1
= 4