You can Download Samacheer Kalvi 11th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 12 Introduction to Probability Theory Ex 12.2
Question 1.
If A and B are mutually exclusive events P(A) = \(\frac{3}{8}\) and P (B) = \(\frac{1}{8}\), then find
(i) P\((\overline{\mathrm{A}})\)
(ii) P(A ∪ B)
(iii) P(\(\overline{\mathrm{A}}\) ∩ B
(iv) P\((\overline{\mathrm{A}} \cup \overline{\mathrm{B}})\)
Solution:
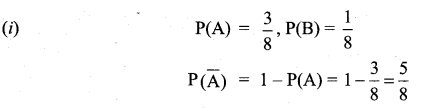

![]()
Question 2.
If A and B are two events associated with a random experiment for which P(A) = 0.35, P(A or B) = 0.85, and P(A and B) = 0.15.
Find (i) P(only B)
(ii) P\((\overline{\mathrm{B}})\)
(iii) P(only A)
Solution:
Given P(A) = 0.35
P(A ∪ B) = 0.85
P(A ∩ B) = 0.15
We know P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
(i.e.,) 0.85 = 0.35 + P(B) – 0.15
⇒ 0.85 – 0.2 = P(B)
(i.e.,) P(B) = 0.65
(i) P(only B ) = P(B) – P(A ∩ B)
= 0.65 – 0.15 = 0.50
(ii) P\((\overline{\mathrm{B}})\) = 1 – P(B) = 1 – 0.65 = 0.35
(iii) P(A only) = P(A) – P(A ∩ B) = 0.35 – 0.15 = 0.20
Question 3.
A die is thrown twice. Let Abe the event, ‘First die shows 5’ and B be the event, ‘second die shows 5’. Find P(A ∪ B).
Solution:
When a die is throw twice
n(s) = 62 = 36
Let A be the event that first die shows 5 and B be the event that second die shows 5 Now A = {(5, 1), (5, 2) (5, 3), (5, 4), (5, 5) (5, 6}
n(A) = 6 ⇒ P(A) = \(\frac{n(\mathrm{A})}{n(\mathrm{S})}=\frac{6}{36}\)
and B = {(1, 5), (2, 5), (3, 5), (4, 5), (5, 5), (6, 5)}
n(B) = 6 ⇒ P(B) = \(\frac{n(\mathrm{B})}{n(\mathrm{S})}=\frac{6}{36}\)
Also A ∩ B = {(5, 5)} ⇒ n (A ∩ B) = 1
P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
= \(\frac{6}{36}+\frac{6}{36}-\frac{1}{36}=\frac{11}{36}\)
![]()
Question 4.
The probability of an event A occurring is 0.5 and B occurring is 0.3. If A and B are mutually exclusive events, then find the probability of
(i) P(A ∪ B)
(ii) P(A ∩ \(\overline{B}\))
(iii)P(\(\overline{A}\) ∩ B)
Solution:
Given P(A) = 0.5, P(B) = 0.3
Also A and B are mutually exclusive. ∴ A ∩ B = Φ
n(A ∩ B) = 0
(i) P (A ∪ B)
P(A ∪B) = P(A) + P(B) – P(A ∩ B)
P(A ∪ B) = P(A) + P(B) – 0 = 0.5 + 0.3 = 0.8
(ii) P(A ∩ B̅)
P(A ∩ B̅) = P(A) – P(A ∩ B) = P(A) – 0
since A and B are mutually exclusive = 0.5
(iii) P(A̅ ∩ B)
P(A̅ ∩ B) = P(B) – P(A ∩ B) = P(B) – 0
since A and B are mutually exclusive = 0.3
Question 5.
A town has 2 fire engines operating independently. The probability that a fire engine is available when needed is 0.96.
(i) What is the probability that a fire engine is available when needed?
(ii) What is the probability that neither is available when needed?

Solution:
(i) Probability that a fire engine is available when needed = P (availability of the first fire engine A or availability of the second fire engine B)
= P(A ∪ B)
= P(A) + P(B) – P (A ∩ B)
= P (A) + P ( B) – P (A) . P (B)
since A and B are independent events
= 0.96 + 0.96 – 0.96 × 0.96
= 2 × 0.96 – (0.96)2
= 0.96 (2 – 0.96)
= 0.96 × 1.04 = 0.9984
(ii) Probability of neither of the fire engine available when needed = Probability of non-availability of the first fire engine and Probability of non-availability of the second fire engine.
= P(A̅ ∩ B̅)
= P(A̅) . P(B̅)
since A and B are independent.
= 0.04 × 0.04
= 0.0016
Question 6.
The probability that a new railway bridge will get an award for its design is 0.48, the probability that it will get an award for the efficient use of materials is 0.36, and that it will get both awards is 0.2. What is the probability, that (i) it will get atleast one of the two awards 00 it will get only one of the awards?
Solution:
Given P(A) = 0.48, P(B) = 0.36 and P(A ∩ B) = 0.2
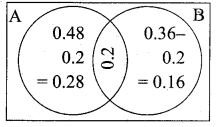
(i) it will get at least one of the two awards
Given the probability that a new railway bridge will get an award for its design is 0.48.
P (A) = 0.48
The probability that it will get an award for the efficient use of materials is 0.36
P (B) = 0.36
The probability that it will get both awards is 0.2
P(A ∩ B) = 0.2
P(atleast one of the two awards) = P(A or B)
= P(A ∪ B)
= P(A) + P(B) – P(A ∩ B)
= 0.48 + 0.36 – 0.2
= 0.84 – 0.20
= 0.64
(ii) P (only one of the awards) = P (only A or only B)
= P [(A ∩ B̅) ∪ (A̅ ∩ B)]
= P (A ∩ B̅) + P (A̅ ∩ B)
A ∩ B and A̅ ∩ B are mutually exclusive
= [P(A) – P(A ∩ B)] + [P(B) – P(A ∩ B)]
= [0.48 – 0.2] + [0.36 – 0.2]
= 0.28 + 0.16
= 0.44
Samacheer Kalvi 11th Maths Solutions Chapter 12 Introduction to Probability Theory Ex 12.2 Additional Problems
Question 1.
A and B are two events associated with random experiment for which P(A) = 0.36, P(A or B) = 0.90 and P(A and B) = 0.25. Find
(i) P(B)
(ii) P\((\overline{\mathrm{A}} \cap \overline{\mathrm{B}})\)
Solution:
(i) Given P(A) = 0.36, P(A ∪ B) = 0.09, P(A ∩ B) = 0.25
P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
(i.e.,) 0.90 = 0.36 + P(B) – 0.25
0.90 = 0.11 + P(B)
∴ P(B) = 0.90 – 0.11 = 0.79
(ii) P\((\overline{\mathrm{A}} \cap \overline{\mathrm{B}})\) = P{(A’ ∪ B)’} (Demorgan Law)
P(A ∪ B)’ = 1 – P(A ∪ B) = 1 – 0.90 = 0.1.
![]()
Question 2.
Given P(A) = 0.5, P(B) = 0.6 and P(A ∩ B) = 0.24. Find
(i) P(A ∪ B)
(ii) P(\(\overline{\mathrm{A}}\) ∩ B)
(iii) P(A ∩ \(\overline{\mathrm{B}}\))
(iv) P(\(\overline{\mathrm{A}} \cup \overline{\mathrm{B}})\)
(v) P\((\overline{\mathrm{A}} \cap \overline{\mathrm{B}})\)
Solution:
(i) P(A) = 0.5, P(B) = 0.6, P(A ∩ B) = 0.24
P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
(i.e.,) P(A ∪ B) = 0.5 + 0.6 – 0.24
= 1.1 – 0.24
= 0.86
∴ P(A ∪ B) = 0.86
(ii) P(\(\overline{\mathrm{A}}\) ∩ B) = P(B) – P(A ∩ B)
= 0.6 – 0.24
= 0.36
(iii) P(A ∩ \(\overline{\mathrm{B}}\)) = P(A) – P(A ∩ B)
= 0.5 – 0.24
= 0.26
(iv) P(\(\overline{\mathrm{A}} \cup \overline{\mathrm{B}})\) = P {(A ∩ B)’} = 1 – P(A ∩ B)
= 1 – 0.24
= 0.76
(v) P\((\overline{\mathrm{A}} \cap \overline{\mathrm{B}})\) = P{A ∪ B)’} = 1 – P(A ∪ B)
= 1 – 0.86
= 0.14.
Question 3.
The probability of an event A occurring is 0.5 and B occurring is 0.3. If A and B are mutually exclusive events, then find the probability of neither A nor B occurring.
Solution:
Given A and B are mutually exclusive and P(A) = 0.5, P(B) = 0.3
∴ P(A ∪ B) = P(A) + P(B) = 0.5 + 0.3 = 0.8
So, P(A’ ∩ B’) = P{(A ∪ B)’} = 1 – P(A ∪ B)
= 1 – 0.8
= 0.2
![]()
Question 4.
The probability that a new ship will get an award for its design is 0.25, the probability that it will get an award for the efficient use of materials is 0.35 and that it will get both awards is 0.15. What is the probability, that (/) it will get atleast one of the two awards (ii) it will get only one of the awards?
Solution:
Probability of getting the award for its design = P(A) = 0.25
Probability of getting the award for the efficient use of materials = P(B) = 0.35
Probability of getting both awards = P(A ∩ B) = 0.15
Now P(A) = 0.25; P(B) = 0.35 and P(A ∩ B) = 0.15
∴ (i) P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
= 0.25 + 0.35 – 0.15
= 0.60 – 0.15
= 0.45
(ii) P(A’ ∩ B’ or B ∩ A’) = P(A ∩ B’) + P(A’ ∩ B)
P(A ∩ B’) = P(A) – P(A ∩ B)
= 0.25 – 0.15
= 0.10
P(A’ ∩ B) = P(B) – P(A ∩ B)
= 0.35 – 0.15
= 0.20
∴ P(A ∩ B’) + P(A’ ∩ B) = 0.10 + 0.20 = 0.30.