Samacheer Kalvi 11th Maths Solutions Chapter 10 Differentiability and Methods of Differentiation Ex 10.5

You can Download Samacheer Kalvi 11th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 10 Differentiability and Methods of Differentiation Ex 10.5

Choose the correct or the most suitable answer from the given four alternative
Question 1.

Solution:
(b)

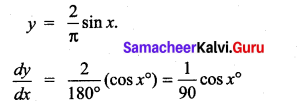
Question 2.
If y = f(x² + 2) and f'(3) = 5, then \(\frac{d y}{d x}\) at x = 1 is …………….
(a) 5
(b) 25
(c) 15
(d) 10
Solution:
(d)

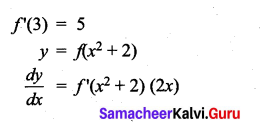
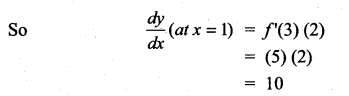
Question 3.
If y = \(\frac{1}{4}\)u⁴, u = \(\frac{2}{3}\)x³ + 5, then \(\frac{d y}{d x}\) is ……………

Solution:
(c)

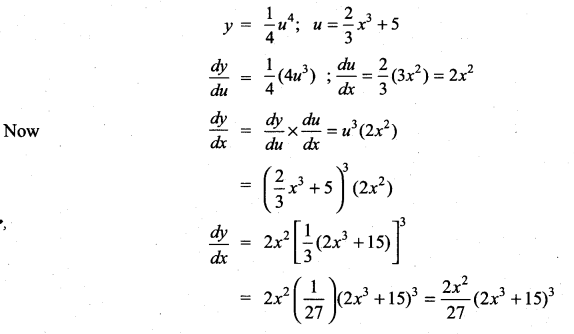
Question 4.
If f(x) = x² – 3x, then the points at which f(x) = f'(x) are …………………..
(a) both positive integers
(b) both negative integers
(c) both irrational
(d) one rational and another irrational
Solution:
(c)
f(x) = x² – 3x
f'(x) = 2x – 3
Given f(x) = f'(x)
⇒ x² – 3x = 2x – 3
⇒ x² – 5x + 3 = 0
x = \(\frac{5 \pm \sqrt{25-12}}{2}=\frac{5 \pm \sqrt{13}}{2}\)
⇒ The roots are irrational

Question 5.
If y = \(\frac{1}{a-z}\), then \(\frac{d z}{d y}\) is ……………….
(a) (a – z)²
(b) -(z – a)²
(c) (z + a)²
(d) -(z + a)²
Solution:
(a)

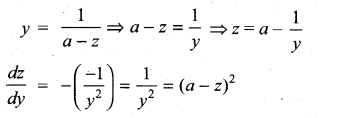
Question 6.
If y = cos (sin x²), then \(\frac{d y}{d x}\) at x = \(\sqrt{\frac{\pi}{2}}\) is …………..
(a) -2
(b) 2
(c) -2\(\sqrt{\frac{\pi}{2}}\)
(d) 0
Solution:
(d)
y = cos (sin x²)
\(\frac{d y}{d x}\) = – sin (sin x²) [cos (x²)] (2x)
∴ \(\frac{d y}{d x}\) at x = \(\sqrt{\frac{\pi}{2}}\) = -sin (1) [0] = 0

Question 7.
If y = mx + c and f(0) = f'(0) = 1, then f(2) is ………………
(a) 1
(b) 2
(c) 3
(d) -3
Solution:
(c)
y = mx + c
Given f(0) = f’ (0) = 1
Let f(x) = mx + c
f'(x) = m
f'(o) = m ⇒ m = 1
f(o) = m × 0 + c
f(o) = c
f(2) = c
f(2) = m × 2 + c
f(2) = 1 × 2 + 1 = 3

Question 8.
If f(x) = x tan^-1x, then f'(1) is ……………
(a) 1 + \(\sqrt{\frac{\pi}{4}}\)
(b) \(\frac{1}{2}+\frac{\pi}{4}\)
(c) \(\frac{1}{2}-\frac{\pi}{4}\)
(d) 2
Solution:
(b)
f(x) = x tan^-1 x

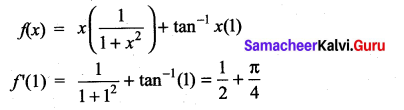
Question 9.
\(\frac{d}{d x}\)(e^x+5logx) is ……………..
(a) e^x.x⁴ (x + 5)
(b) e^x.x (x + 5)
(c) e^x + \(\frac{5}{x}\)
(d) e^x – \(\frac{5}{x}\)
Solution:
(a)
y = e^x+5logx = e^x.e^5logx = e^x.e^logx5
= x⁵ e^x
∴ \(\frac{d y}{d x}\) = x⁵ (e^x) + e^x (5x⁴)
= e^x. x⁴ (x + 5)

Question 10.
If the derivative of (ax – 5) e^3x at x = 0 is -13, then the value of a is …………….
(a) 8
(b) -2
(c) 5
(d) 2
Solution:
(d)
Let y = (ax – 5) e^3x
\(\frac{\mathrm{d} \mathrm{y}}{\mathrm{d} x}\) = (ax – 5) e^3x (3) + e^3x (a × 1 – 0)
= 3 e^3x (ax – 5) + e^3x × a
\(\frac{\mathrm{d} \mathrm{y}}{\mathrm{d} x}\) = e^3x (3ax – 15 + a) ……….. (1)
Given at x = 0, \(\frac{\mathrm{d} \mathrm{y}}{\mathrm{d} x}\) = – 13
(1) ⇒ – 13 = e^{3 × 0} (3a × 0 – 15 + a)
– 13 = e⁰ (0 – 15 + a)
– 13 = – 15 – a
a = 15 – 13 = 2
a = 2

Question 11.
x = \(\frac{1-t^{2}}{1+t^{2}}\), y = \(\frac{2 t}{1+t^{2}}\) then \(\frac{d y}{d x}\) is …………..

Solution:
(c)
Given x = \(\frac{1-t^{2}}{1+t^{2}}\) and y = \(\frac{2 t}{1+t^{2}}\)
when we put t = tan θ
Then x = cos 2θ and y = sin 2θ

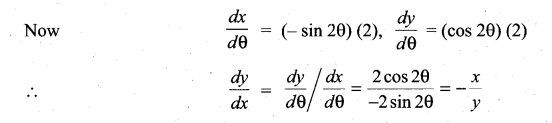
Question 12.
If x = a sin θ and y = b cos θ, then \(\frac{d^{2} y}{d x^{2}}\) is …………..

Solution:
(c)

Question 13.
The differential coefficient of log₁₀x with respect to log_x 10 is …………….
(a) 1
(b) -(log₁₀x)²
(c) (log_x 10)²
(d) \(\frac{x^{2}}{100}\)
Solution:
(b)

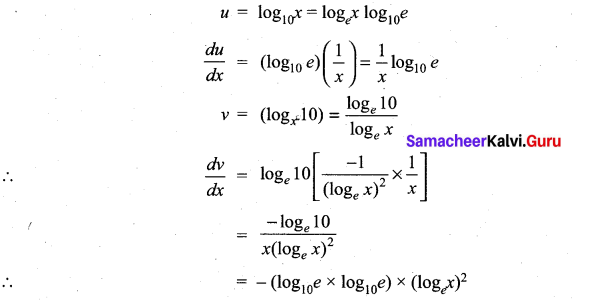
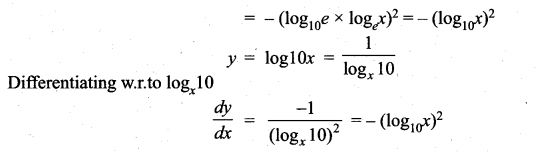
Question 14.
If f(x) = x + 2, then f'(f(x)) at x = 4 is ……………..
(a) 8
(b) 1
(c) 4
(d) 5
Solution:
(b)
f(x) = x + 2
f'(x) = 1
f'(x) (at x = 4) = 1

Question 15.
If y = \(\frac{(1-x)^{2}}{x^{2}}\), then \(\frac{d y}{d x}\) is ………………

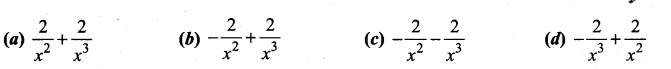
Solution:
(d)

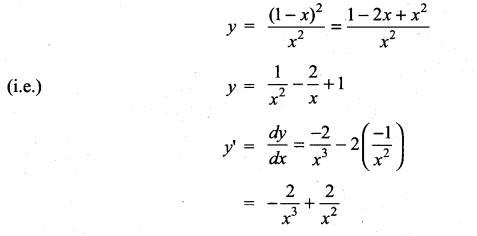
Question 16.
If pv = 81, then \(\frac{d p}{d v}\) at v = 9 is ………….
(a) 1
(b) -1
(c) 2
(d) -2
Solution:
(b)

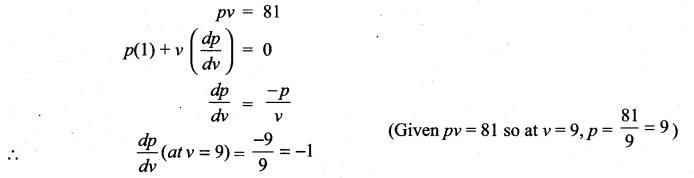
Question 17.
If f(x) = 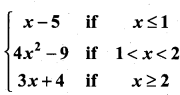then the right hand derivative of f(x) at x = 2 is ……………….
(a) 0
(b) 2
(c) 3
(d) 4
Solution:
(c)

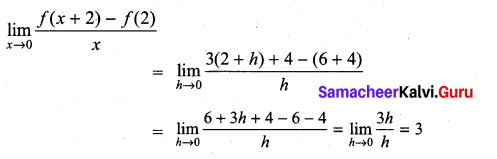
Question 18.
It is given that f'(a) exists, then 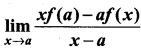is ……………..
(a) f(a) – af'(a)
(b) f ‘(a)
(c) -f ‘(a)
(d) f(a) + af ‘(a)
Solution:
(a)

Question 19.
If f(x) = 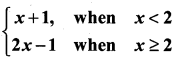then f ‘(2) is ………………
(a) 0
(b) 1
(c) 2
(d) does not exist
Solution:
(d)

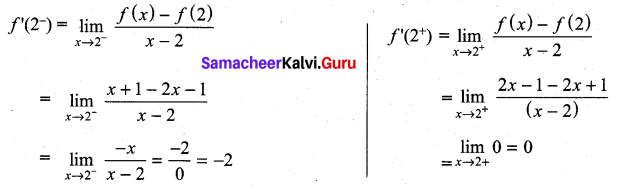
∴ f ‘(2) does not exist

Question 20.
If g(x) = (x² + 2x + 3) f(x) and f(0) = 5 and then g ‘(θ) is ……………
(a) 20
(b) 22
(c) 18
(d) 12
Solution:
(b) 22

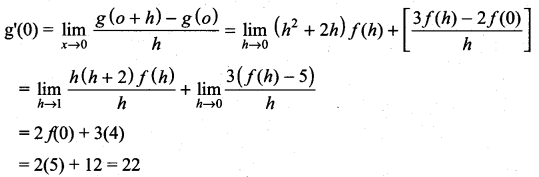
Question 21.
If f(x) = 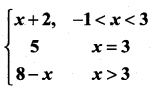, then at x = 3, f ‘(x) is ………………
(a) 1
(b) -1
(c) 0
(d) does not exist
Solution:
(d)

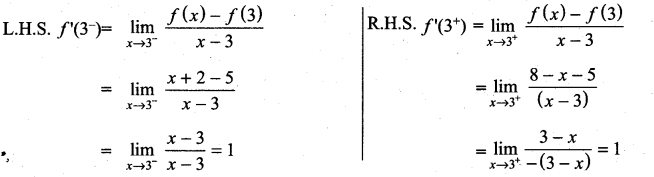
as LHS ≠ RHS limit does not exist

Question 22.
The derivative of f(x) = x|x| at x = -3 is …………..
(a) 6
(b) -6
(c) does not exist
(d) 0
Solution:
(a)
f(x) = x |x|
when x < 0 we have |x| = – x
∴ At x = – 3, f(x) = x (- x) = – x²
f'(x) = – 2x
f’ (- 3) = – 2 × – 3 = 6

Question 23.
If f(x) = 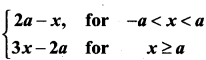, then which one of the following is true?
(a) f(x) is not differentiable at x = a
(b) f(x) is discontinuous at x = a
(c) f(x) is continuous for all x in R
(d) f(x) is differentiable for all x ≥ a
Solution:
(a)

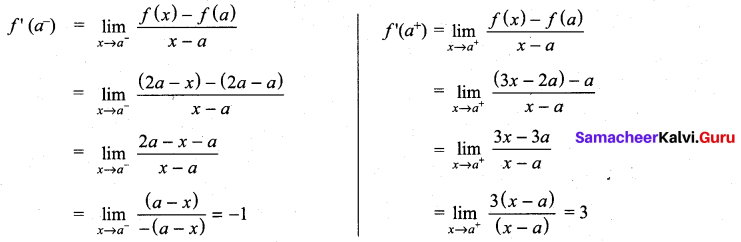
f(x) is not differentiable at x = a

Question 24.
If f(x) = 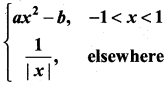is differentiable at x = 1, then ………………

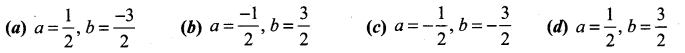
Solution:
(c)

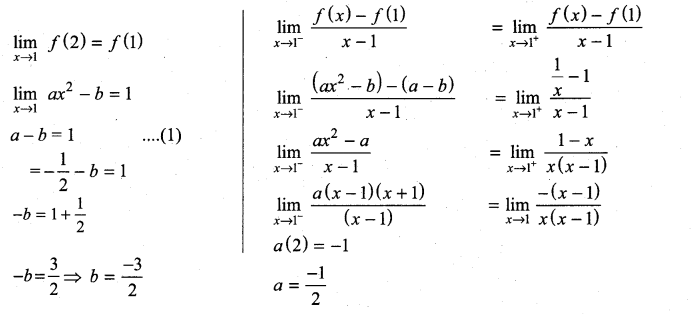
Question 25.
Then number of points in R in which the function f(x) = |x – 1| + |x – 3| + sin x is not differentiable, is ……………..
(a) 3
(b) 2
(c) 1
(d) 4
Solution:
(b) 2
f(x) = |x – 1| + |x – 3| + sin x
f(x) is not differentiable at x = 1 and x = 3
Since at x = 1 and x = 3,
f(x) will have vertical tangent
∴ Number of points = 2