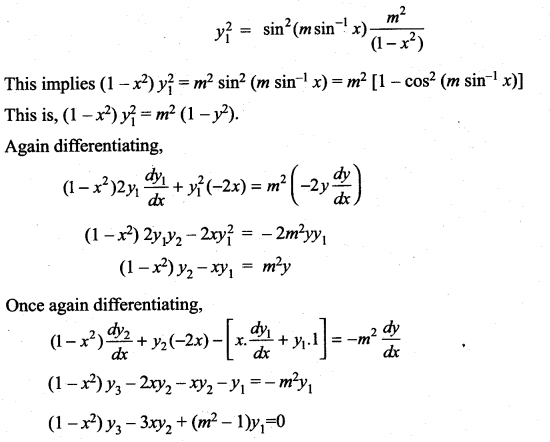You can Download Samacheer Kalvi 11th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 10 Differentiability and Methods of Differentiation Ex 10.4
Find the derivatives of the following functions
Question 1.
y = xcos x
Solution:
y = xcos x
Taking log on both sides
log y = log xcos x = cos x log x
differentiating w.r.to x we get
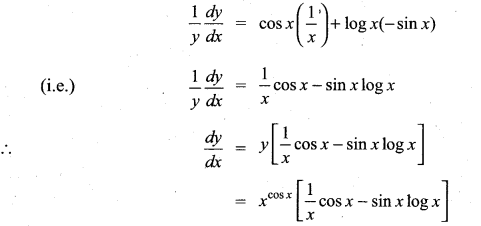
Question 2.
y = xlogx + (logx)x
Solution:
y = xlogx + (logx)x
Let y = u + v
Then \(\frac{d y}{d x}=\frac{d u}{d x}+\frac{d v}{d x}\)
u = xlogx
Taking log on both sides
log u = log x log x = log (x)2
differentiating w.r.to x

Taking log on both sides
log u = log (logx)x = x log (log x)
differentiating w.r.to x
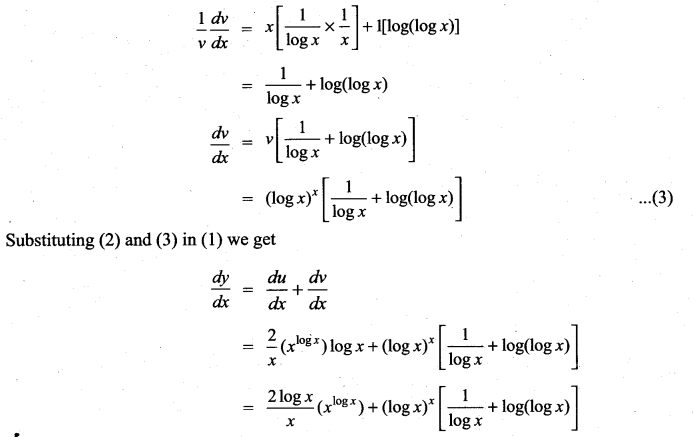
Question 3.
\(\sqrt{x y}\) = e(x – y)
Solution:
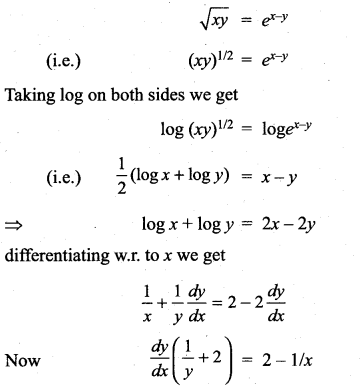
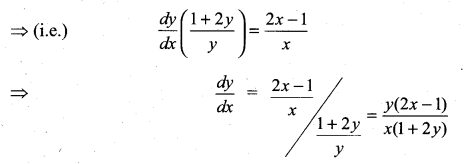
![]()
Question 4.
xy = yx
Solution:
xy = yx
Taking log on both sides
logxy = logyx
(i.e.) y log x = x log y
differentiating w.r.to x
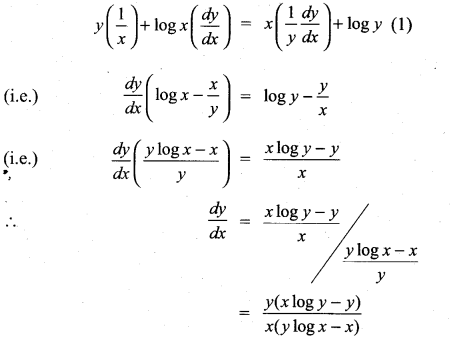
Question 5.
(cos x)log x
Solution:
y = (cos x)log x
Taking log on both sides
log y = log (cos x)log x = log x (log cos x)
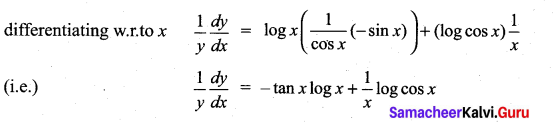
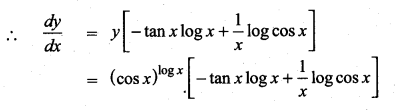
Question 6.
\(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}\) = 1
Solution:
\(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}\) = 1
Differentiating w.r.to x

Question 7.
\(\sqrt{x^{2}+y^{2}}=\tan ^{-1}\left(\frac{y}{x}\right)\)
Solution:
\(\sqrt{x^{2}+y^{2}}=\tan ^{-1}\left(\frac{y}{x}\right)\)
Differentiating w.r.to x
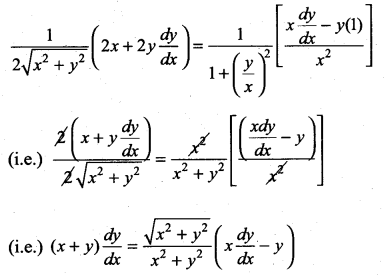
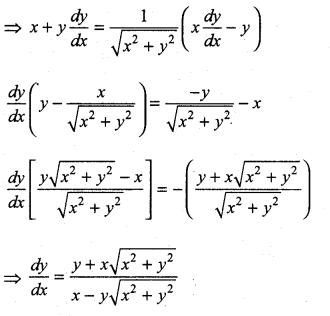
![]()
Question 8.
tan (x + y) + tan (x – y) = x
Solution:
tan (x + y) + tan (x – y) = x
Differentiating w.r.to x we get
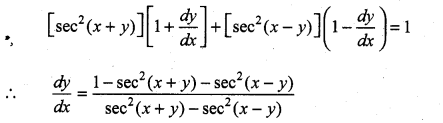
Question 9.
If cos (xy) = x, show that \(\frac{d y}{d x}=\frac{-(1+y \sin (x y))}{x \sin x y}\)
Solution:
cos (xy) = x
Differentiating w.r.to x

Question 10.
\(\tan ^{-1} \sqrt{\frac{1-\cos x}{1+\cos x}}\)
Solution:
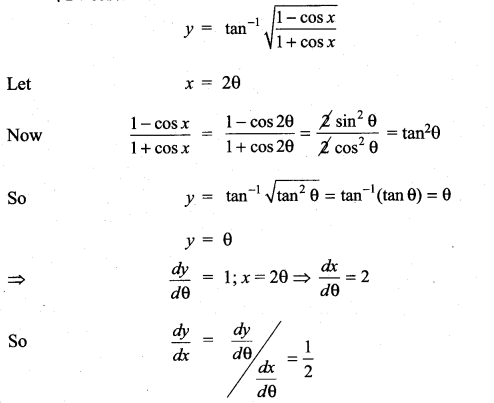
Question 11.
\(\tan ^{-1}\left(\frac{6 x}{1-9 x^{2}}\right)\)
Solution:
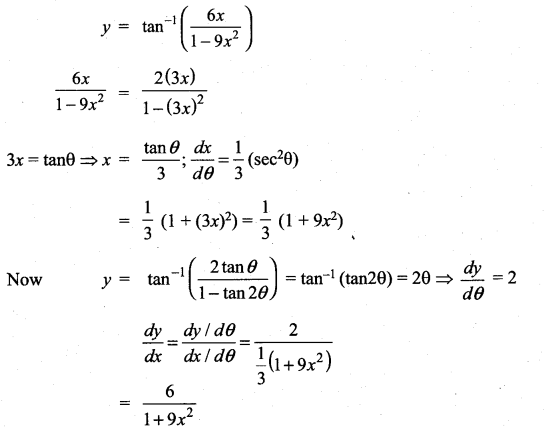
Question 12.
cos [2 \(\tan ^{-1} \sqrt{\frac{1-x}{1+x}}\)]
Solution:
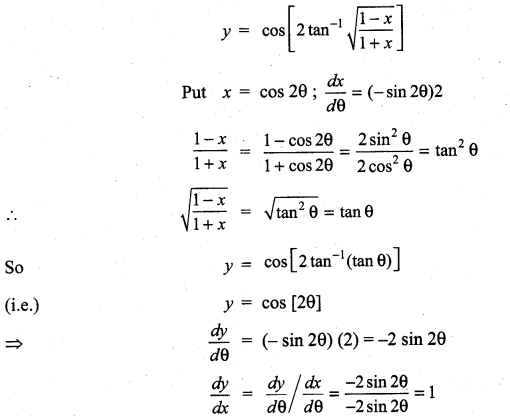
Question 13.
x = a cos3t; y = a sin2t
Solution:
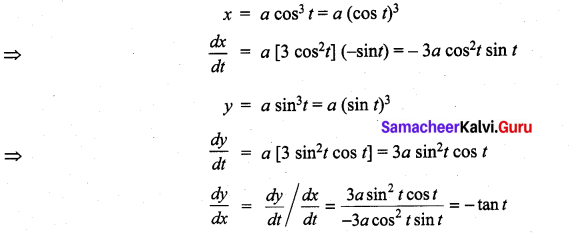
Question 14.
x = a (cos t + t sin t); y = a [sin t – t cos t]
Solution:
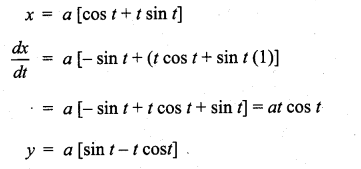
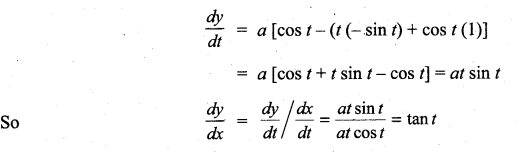
Question 15.
x = \(\frac{1-t^{2}}{1+t^{2}}\); y = \(\frac{2 t}{1+t^{2}}\)
Solution:

![]()
Question 16.
\(\cos ^{-1}\left(\frac{1-x^{2}}{1+x^{2}}\right)\)
Solution:
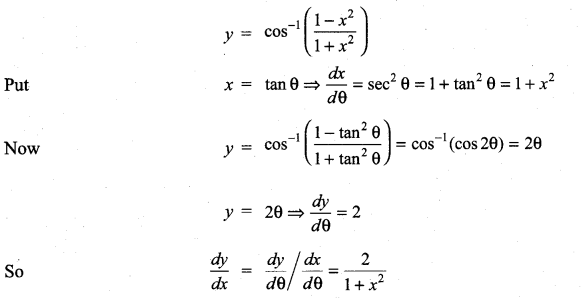
Question 17.
sin-1 (3x – 4x3)
Solution:
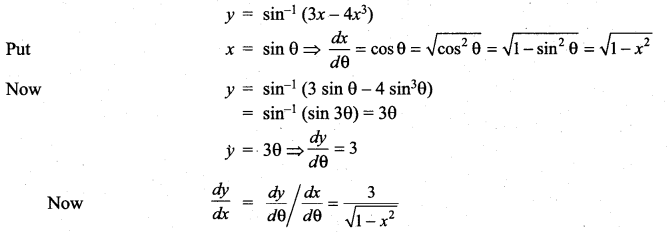
Question 18.
\(\tan ^{-1}\left(\frac{\cos x+\sin x}{\cos x-\sin x}\right)\)
Solution:
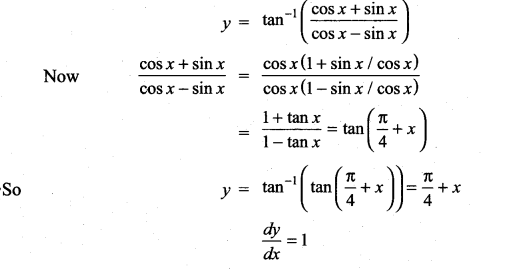
Question 19.
Find the derivative of sin x2 with respect to x2
Solution:

Question 20.
Find the derivative of \(\sin ^{-1}\left(\frac{2 x}{1+x^{2}}\right)\) with respect to tan-1 x.
Solution:
Let u = \(\sin ^{-1}\left(\frac{2 x}{1+x^{2}}\right)\) and v = tan-1 x
Now we have to find \(\frac{d u}{d v}\)
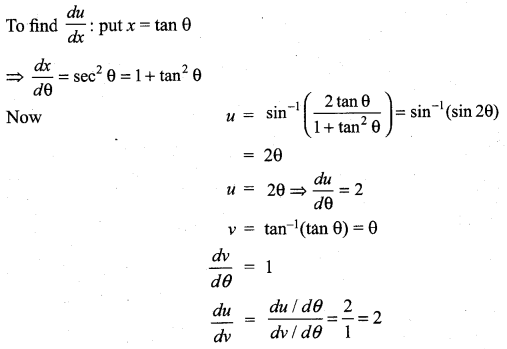
![]()
Question 21.
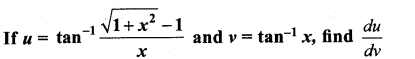
Solution:

Question 22.
Find the derivative with 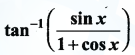 with respect to
with respect to 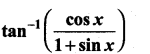
Solution:
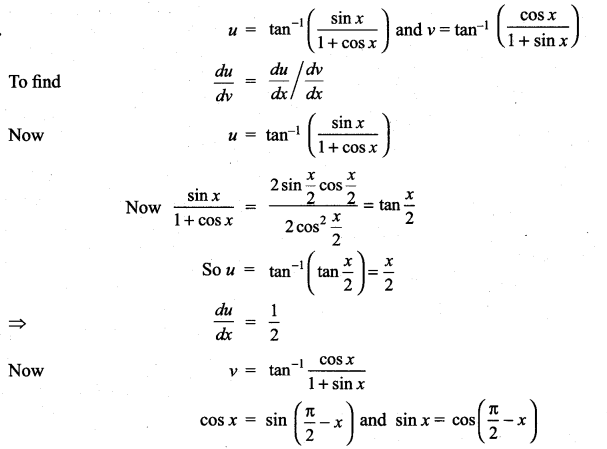
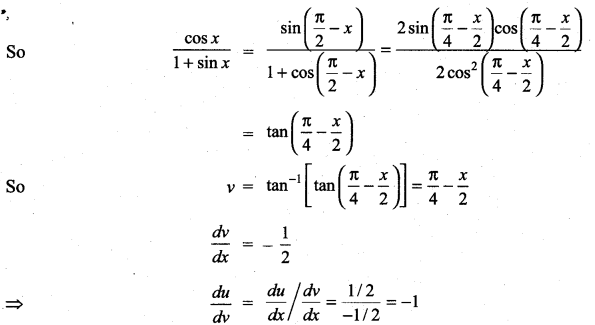
Question 23.
If y = sin-1 then find y”.
Solution:
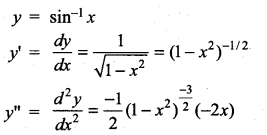
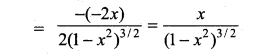
Question 24.
If y = etan-1x, show that (1 + x2) y” + (2x – 1) y’ = 0
Solution:
y = etan-1x
y’ = etan-1 × \(\frac{1}{1+x^{2}}\)
(1 + x2) y’ = etan-1x
(1 + x2) y’ = y
Differentiating with respect to x
(1 + x2) y” + y’ (0 + 2x) = y’
(1 + x2) y” + 2xy’ – y’ = 0
(1 + x2) y” + (2x – 1) y’ = 0
Question 25.
If y = \(\frac{\sin ^{-1} x}{\sqrt{1-x^{2}}}\) show that (1 – x2) y2 – 3xy1 – y = 0
Solution:

-xy + (1 – x2) y1 = 1
differentiating both sides again w.r.to x
-[x y1 + y (1)] + (1 – x2) (y2) + y1 (-2x) = 0
(i.e.) -xy1 – y + (1 – x2) y2 – 2xy1 = 0
(1 – x2) y2 – 3xy1 – y = 0
Question 26.
If x = a (θ + sin θ), y = a (1 – cos θ) then prove that at θ = \(\frac{\pi}{2}\), y” = \(\frac{1}{a}\)
Solution:
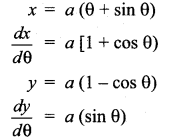

![]()
Question 27.
If sin y = x sin (a + y) Then prove that \(\frac{d y}{d x}=\frac{\sin ^{2}(a+y)}{\sin a}\), a ≠ nπ
Solution:
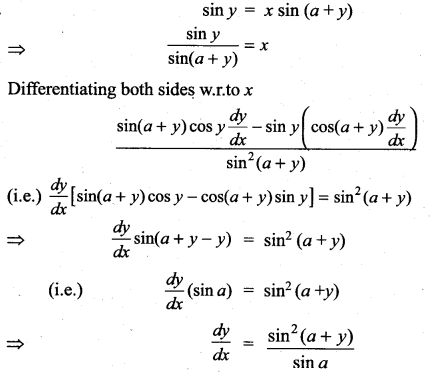
Question 28.
If y = (cos-1 x)2, prove that (1 – x2) \(\frac{d^{2} y}{d x^{2}}-x \frac{d y}{d x}\) – 2 = 0. Hence find y2 when x = 0.
Solution:

Samacheer Kalvi 11th Maths Solutions Chapter 10 Differentiability and Methods of Differentiation Ex 10.4 Additional Problems
Question 1.
If y = A cos 4x + B sin 4x, A and B are constants then Show that y2 + 16y = 0
Solution:
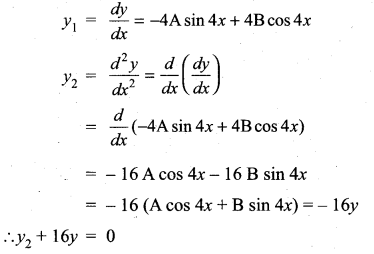
![]()
Question 2.
If y = cos (m sin-1 x), prove that (1 – x2) y3 – 3xy2 + (m2 – 1) y1 = 0
Solution:
We have y = cos (m sin-1 x)
y1 = sin (m sin-1x). \(\frac{m}{\sqrt{1-x^{2}}}\)