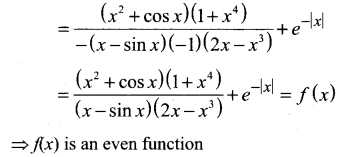You can Download Samacheer Kalvi 11th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 1 Sets Ex 1.5
Choose the correct or the most suitable answer.
Question 1.
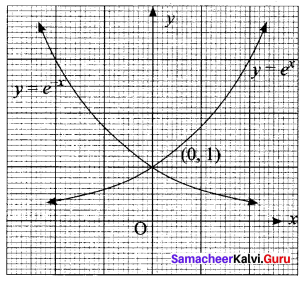
If A = {(x, y) : y = ex ; x ∈ R } and B = {(x, y) : y = e-x, x ∈ R } then n(A ∩ B)
(a) Infinity
(b) 0
(c) 1
(d) 2
Solution:
(c) 1
Hint.
A∩B = (0, 1)
n(A∩B) = 1
Question 2.
IfA {(x, y) : y = sin x, x ∈ R) and 8= (x, y) : y = cos x, x ∈ R) then A∩B contains ……..
(a) no element
(b) infinitely many elements
(c) only one element
(d) cannot be determined.
Solution:
(b) infinitely many elements
![]()
Question 3.
The relation R defined on a set A = {0, -1, 1, 2} by xRy if |x2 +y2| ≤ 2, then which one of the following is true?
(a) R = {(0, 0), (0, -1), (0, 1), (-1, 0), (-1, 1), (1, 2), (1, 0)}
(b) R = {(0, 0), (0, -1), (0, 1), (-1, 0), (1, 0)
(c) Domain of R is {0, -1, 1, 2}
Solution:
(a) Range of R is {0, -1, 1}
Hint.
Given A = {0, -1, 1, 2 }
the relation R is given by x R y = |x2 + y2| ≤ 2
∴ x, y must be 0 or 1
∴ Range of R is {0, – 1 , 1 }
Question 4.
If f(x) = |x – 2| + |x + 2|, x ∈ R, then
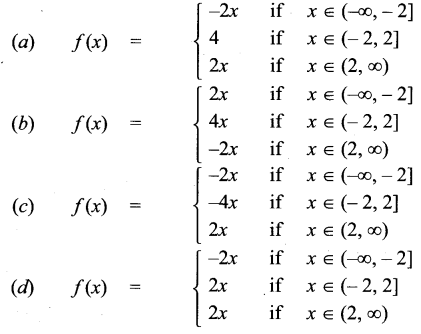
Solution:
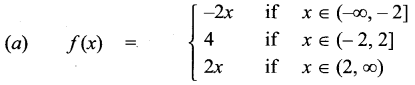
Hint.
f(x) = |x – 2| + |x + 2|
![]()
Question 5.
Let R be the set of all real numbers. Consider the following subsets of the plane R x R: S = {(x, y): y = x + 1 and 0 < x < 2} and T = {(x, y) : x – y is an integer} Then which of the following is true?
(a) T is an equivalence relation but S is not an equivalence relation.
(b) Neither S nor T is an equivalence relation
(c) Both S and T are equivalence relations
(d) S is an equivalence relation but T is not an equivalence relation.
Solution:
(a) T is an equivalence relation but S is not an equivalence relation.
Hint.
Given R is the set of all real numbers
S = { (x, y): y = x + 1 and 0 < x < 2}
T = { (x, y): x – y is an integer} are subsets of R × R
s = { (x, y): y = x + 1 and 0 < x < 2} for x ∈ R,
x = x + 1 is not possible. ∴ (x , x) ∉ S
Hence S does not satisfy the reflexive property
∴ S is not an equivalence relation
T = {(x, y): x – y is an integer}
Reflexive:
For x ∈ R, we have x – x = 0 is an integer.
∴ (x,x)∈T forall X∈ R
Hence T satisfies reflexive property
Symmetric:
Let (x, y) ∈ T, then x – y
⇒ – (x – y) is an integer
⇒ y – x is an integer
⇒ (y, x) ∈ T
∴ T satisfies the symmetric property
Transitive:
Let (x, y), (y, z) ∈ T then x – y and y – z are integers.
⇒ x – y + y – z is an integer
⇒ x – z is an integer
⇒ (x, z) ∈ T
∴ T satisfies the transitive property
we have proved T is reflexive, symmetric, and transitive.
Thus T is an equivalence relation.
![]()
Question 6.
Let A and B be subsets of the universal set N, the set of natural numbers. Then
A’ ∪ [(A ∩ B) ∪ B’] is ………
(a) A
(b) A’
(c) B
(d) N
Solution:
(d) N
Hint.
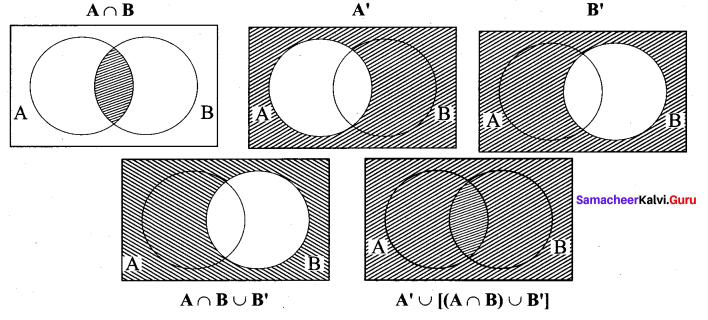
Question 7.
The number of students who take both the subjects Mathematics and Chemistry is 70. This represents 10% of the enrollment in Mathematics and 14% of the enrollment in Chemistry. How many students take at least one of these two subjects?
(a) 1120
(b) 1130
(c) 1100
(d) insufficient data
Solution:
(b) 1130
Hint.
Let M denotes Mathematics students
C denotes Chemistry students
Given n(M ∩ C) = 70
10 % of the enrolement in Mathematics
Out of 100 enrolement 10 students take mathematics
∴ Number of Mathematics students n (M) = \(\frac{100}{10}\) × 70
n (M ) = 700
Number of Chemistry students n(C) = \(\frac{100}{14}\) × 70
n (C) = 500
∴ n(M ∪ C) = n(M) + n(C) – n(M ∩ C)
= 700 + 500 – 70
= 1200 – 70
= 1130
The number of students take atleast one of the subject mathematics or Chemistry = 1130
![]()
Question 8.
If n[(A × B) ∩ (A × C)] = 8 and n(B ∩ C) = 2 , then n(A) is
(a) 6
(b) 4
(c) 8
(d) 16
Solution:
(b) 4
![]()
Question 9.
If n(A) = 2 and n(B ∪ C) = 3, then n[(A × B) ∪ (A × C)] is …….
(a) 23
(b) 32
(c) 6
(d) 5
Solution:
(c) 6
Hint.
Given n (A) = 2 and n(B ∪ C) = 3
n[(A × B) ∪ (A × C)] = n[A × ( B ∪ C ) ]
A × (B ∪ C) = (A × B) ∪ (A × C)
= n(A) . n(B ∪ C)
= 2 × 3 = 6
Question 10.
If two sets A and B have 17 elements in common, then the number of elements common to the set A × B and B × A is
(a) 217
(b) 172
(c) 34
(d) insufficient data
Solution:
(b) 172
Hint.
n (A ∩ B) = 17
So n [(A × B) ∩ (B × A)]
= n(A ∩ B) × n(B ∩ A) = 17 × 17 = 172
![]()
Question 11.
For non-empty sets A and B, if A ⊂ B then (A × B) ∩ (B × A) is equal to ……….
(a) A ∩ B
(b) A × A
(c) B × B
(d) None of these
Solution:
(b) A × A
Hint.
Given A ⊂ B, take A = { 1, 2 } and B = { 1, 2 , 3 }
A × B = {1, 2} × {1, 2, 3}
A × B = {(1, 1), (1, 2), (1, 3), (2, 1), (2, 2), (2, 3)}
B × A = {1, 2, 3} × {1, 2}
B × A = {(1, 1), (1, 2), (2, 1), (2, 2), (3, 1), (3, 2)}
(A × B) ∩ (B × A) = {(1, 1), (1, 2), (1, 3), (2, 1), (2, 2), (2, 3)} ∩ {(1, 1), (1, 2), (2, 1),
(2, 2), (3, 1), (3, 2)}
(A × B) ∩ (B × A) = {(1, 1), (1, 2), (2, 1), (2, 2)}
A × A = {1, 2} × {1, 2}
A × A = { (1, 1), (1, 2), (2, 1), (2, 2) }
(A × B) × (B × A) = A × A
Question 12.
The number of relations on a set containing 3 elements is
(a) 9
(b) 81
(c) 512
(d) 1024
Solution:
(c) 512
Hint.
Number of relations = 2n2 = 232 = 29 = 512
![]()
Question 13.
Let R be the universal relation on a set X with more than one element. Then R is
(a) Not reflexive
(b) Not symmetric
(c) Transitive
(d) None of the above
Solution:
(c) Transitive
Question 14.
Let X = {1, 2, 3, 4} and R = {(1, 1), (1, 2), (1, 3), (2, 2), (3, 3), (2, 1), (3, 1), (1,4), (4, 1)}. Then R is ……..
(a) Reflexive
(b) Symmetric
(c) Transitive
(d) Equivalence
Solution:
(b) Symmetric
Hint.
x = {1, 2, 3, 4}
R = { (1, 1) , (1, 2), (1, 3), (2, 2), (3, 3), (2, 1), (3, 1), (1, 4), (4, 1)}
![]()
Question 15.

Solution:
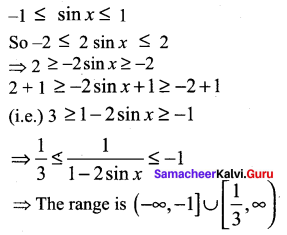
Question 16.
![]()
Solution:
(c) [0, 1)
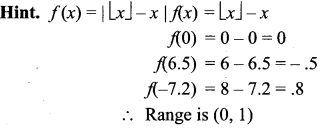
Question 17.
The rule f(x) = x2 is a bijection if the domain and the co-domain are given by …..
(a) R,R
(b) R, (0, ∞)
(c) (0, ∞), R
(d) [0, ∞), [0, ∞)
Solution:
(d) [0, ∞), [0, ∞)
![]()
Question 18.
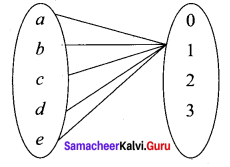
The number of constant functions from a set containing m elements to a set containing n elements is
(a) mn
(b) m
(c) n
(d) m + n
Solution:
(c) n
Question 19.
The function f: [0, 2π] ➝ [-1, 1] defined by f(x) = sin x is
(a) One to one
(b) Onto
(c) Bijection
(d) Cannot be defined
Solution:
(b) Onto
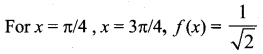
So it is not one-to-one
So it is an onto function
![]()
Question 20.
If the function f : [-3, 3] ➝ S defined by f(x) = x2 is onto, then S is ………
(a)[-9, 9]
(b) R
(c) [-3, 3]
(d) [0, 9]
Solution:
(d) [0, 9]
Question 21.
Let X = {1, 2, 3, 4}, Y = {a, b, c, d) and f = {(1, a), (4, b), (2, c), (3, d) (2, d)}. Then f is ………
(a) An one-to-one function
(b) An onto function
(c) A function which is not one-to-one
(d) Not a function
Solution:
(d) Not a function
Hint.
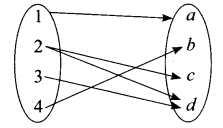
Since the element 2 has two images, it is not a function
Question 22.
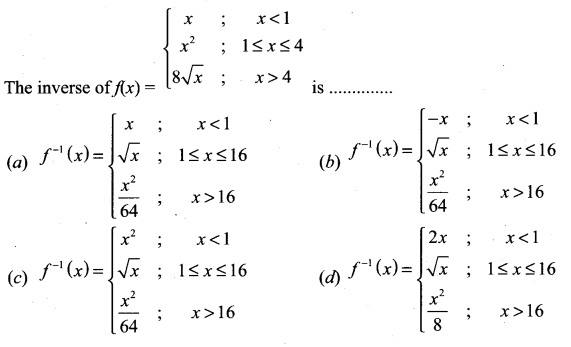
Solution:
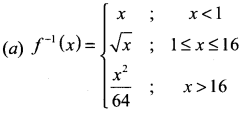
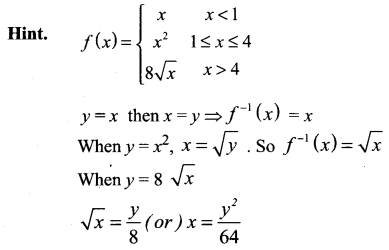

![]()
Question 23.
Let f : R ➝ R be defined by f(x) = 1 – |x|. Then the range of f is ………
(a) R
(b) (1, ∞)
(c) (-1, ∞)
(d) (-∞, 1]
Solution:
(d) (-∞, 1]
Hint.
f(x) = 1 – |x|
When x = 0, f(0) = 1 – 0 = 1
When x = – 2 , f(-2) = 1 – |- 2| = 1 – 2 = -1
When x = – 5 , f(-5) = 1 – |- 5| = 1 – 5 = -4
∴ Range of f is (- ∞, 1]
![]()
Question 24.
The function f : R ➝ R is defined by f(x) = sin x + cos x is ……
(a) An odd function
(b) Neither an odd function nor an even function
(c) An even function
(d) Both odd function and even function
Solution:
(b) Neither an odd function nor an even function
Question 25.
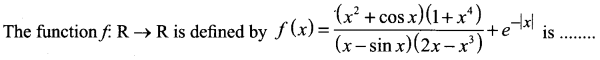
(a) An odd function
(b) Neither an odd function nor an even function
(c) An even function
(d) Both odd function arid even function
Solution:
(c) An even function