You can Download Samacheer Kalvi 10th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 7 Mensuration Ex 7.1
Question 1.
The radius and height of a cylinder are in the ratio 5:7 and its curved surface area is 5500 sq.cm. Find its radius and height.
Solution:
r = 5x
h = 7x
CSA of a cylinder = 2πrh
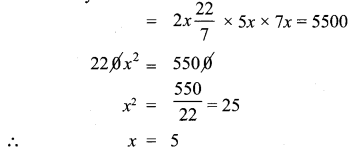
∴ Radius = 5 × 5 = 25 cm
height = 7 × 5 = 35 cm
![]()
Question 2.
A solid iron cylinder has total surface area of 1848 sq.m. Its curved surface area is five – sixth of its total surface area. Find the radius and height of the iron cylinder.
The external radius and the length of a hollow
Solution:

Question 3.
The external radius and the length of a hollow wooden log are 16 cm and 13 cm respectively. If its thickness is 4 cm then find its T.S.A.
Solution:
R = 16 cm
r = R – thickness
r = 12 cm
= 16 – 4 = 12 cm
h = 13 cm
Total surface area of hollow cylinder = 2π(R + r) (R – r + h) sq. units.
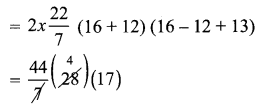
∴ T.S.A = 2992 cm2
![]()
Question 4.
A right angled triangle PQR where ∠Q = 90° is rotated about QR and PQ. If QR = 16 cm and PR = 20 cm, compare the curved surface areas of the right circular cones so formed by the triangle.
Solution:
When it is rotated about PQ the C.S.A of the cone formed = πrl.
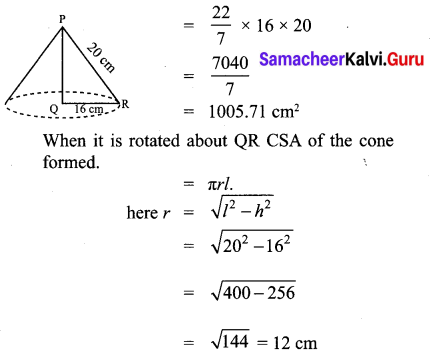
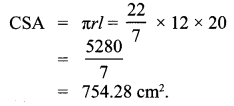
1005.71 > 754.28
∴ CSA of the cone rotated about its PQ is larger than the CSA of the cone rotated about QR.
Question 5.
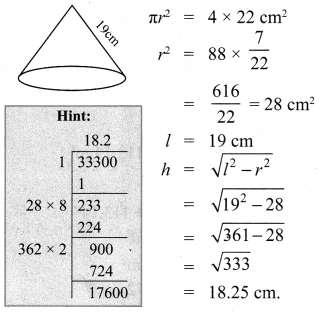
4 persons live in a conical tent whose slant height is 19 cm. If each person require 22 cm2 of the floor area, then find the height of the tent.
Solution:
Base area of the cone = πr2 = sq units.
Question 6.
A girl wishes to prepare birthday caps in the form of right circular cones for her birthday party, using a sheet of paper whose area is 5720 cm2, how many caps can be made with radius 5 cm and height 12 cm.
Solution:

![]()
Question 7.
The ratio of the radii of two right circular cones of same height is 1 : 3. Find the ratio of their curved surface area when the height of each cone is 3 times the radius of the smaller cone.
Solution:


Question 8.
The radius of a sphere increases by 25%. Find the percentage increase in its surface area.
Solution:
Surface area of sphere A = 4πr2
New radius = r’ = 1.25r,
[∵ r + 0.25r] (25% = 0.25)
New surface area = A’ = 4π(r’)2
= 4π(1.25 r)2
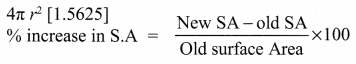

Question 9.
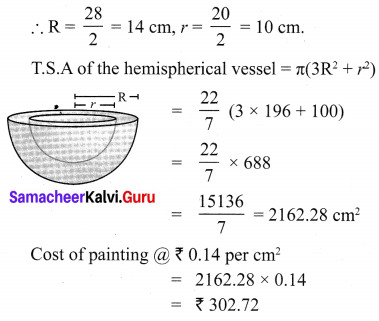
The internal and external diameters of a hollow hemispherical vessel are 20 cm and 28 cm respectively. Find the cost to paint the vessel all over at ₹ 0.14 per cm2.
Solution:
External diameter D = 28 cm
Internal diameter d = 20 cm
![]()
Question 10.
The frustum shaped outer portion of the table lamp has to be painted including the top part. Find the total cost of painting the lamp if the cost of painting 1 sq.cm is ₹ 2.

Solution:
Here given that R = 12 m
r = 6 m
h = 8 m

