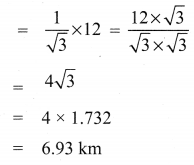You can Download Samacheer Kalvi 10th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 6 Trigonometry Ex 6.4
Question 1.
From the top of a tree of height 13 m the angle of elevation and depression of the top and bottom of another tree are 45° and 30° respectively. Find the height of the second tree. (\(\sqrt{3}\) = 1.732)
Solution:

![]()
Question 2.
A man is standing on the deck of a ship, which is 40 m above water level. He observes the angle of elevation of the top of a hill as 60° and the angle of depression of the base of the hill as 30°. Calculate the distance of the hill from the ship and the height of the hill. (\(\sqrt{3}\) = 1.732)
Solution:
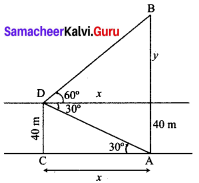
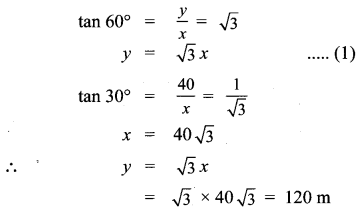
∴ The height of the hill = 120 + 40 = 160 m
The distance of the hill from the ship is AC = x = \(40 \sqrt{3}\) m = 69.28 m
Question 3.
If the angle of elevation of a cloud from a point ‘h’ metres above a lake is θ1 and the angle of depression of its reflection in the lake is θ2. Prove that the height that the cloud is located from the ground is \(\frac{h\left(\tan \theta_{1}+\tan \theta_{2}\right)}{\tan \theta_{2}-\tan \theta_{1}}\)
Solution:
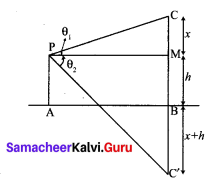
Let AB be the surface of the lake and let p be the point of observation such that AP = h meters.
Let C be the position of the cloud and C’ be its reflection in the lake. Then CB = C’B.
Let PM be ⊥r from P on CB
Then ∠CPM = θ1, and ∠MPC = θ2
Let CM = x.
Then CB = CM + MB = CM + PA
= x + h
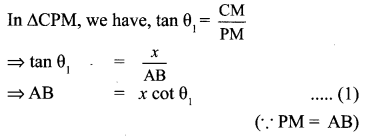
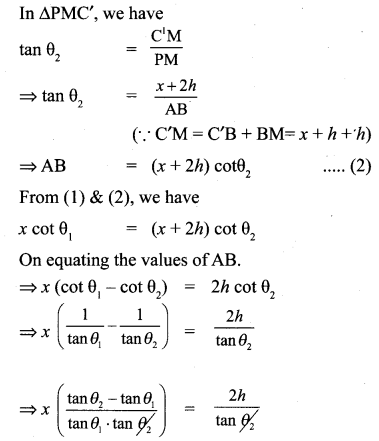

Hence proved
![]()
Question 4.
The angle of elevation of the top of a cell phone tower from the foot of a high apartment is 60° and the angle of depression of the foot of the tower from the top of the apartment is 30°. If the height of the apartment is 50 m, find the height of the cell phone tower. According to radiations control norms, the minimum height of a cell phone tower should be 120 m. State if the height of the above mentioned cell phone tower meets the radiation norms.
Solution:
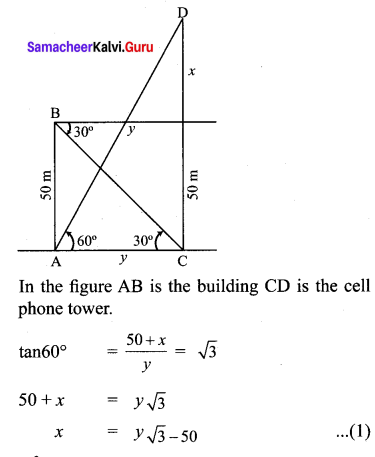

Since 150m > 120m, yes the height of the above mentioned tower meet the radiation norms.
Question 5.
The angles of elevation and depression of the top and bottom of a lamp post from the top of a 66 m high apartment are 600 and 30° respectively. Find
(i) The height of the lamp post.
(ii) The difference between height of the lamp post and the apartment.
(iii) The distance between the lamp post and the apartment. (\(\sqrt{3}\) = 1.732)
Solution:
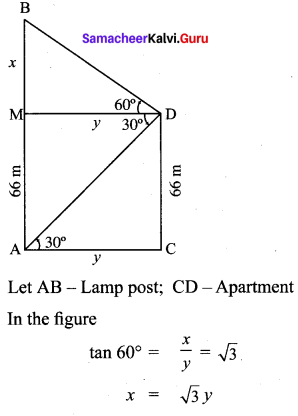

= 114.312 m
![]()
Question 6.
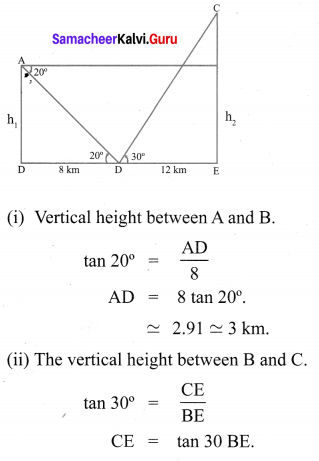
Three villagers A, B and C can see each T other across a valley. The horizontal distance between A and B is 8 km and the horizontal distance between B and C is 12 km. The angle of depression of B from A is 20° and the angle of elevation of C from B is 30° . Calculate :

(i) the vertical height between A and B.
(ii) the vertical height between B and C. (tan20° = 0.3640, \(\sqrt{3}\) = 1.732)
Solution: